新疆维吾尔自治区乌鲁木齐市2020届九年级上学期数学期末考试试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. 下列图形中,既是中心对称图形,又是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球,下列事件是必然事件的是( )A、摸出的三个球中至少有一个球是黑球 B、摸出的三个球中至少有一个球是白球 C、摸出的三个球中至少有两个球是黑球 D、摸出的三个球中至少有两个球是白球3. 一元二次方程 的根的情况是A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断4. 如图,在 中, 所对的圆周角 ,若 为 上一点, ,则 的度数为( )
2. 袋子中装有4个黑球和2个白球,这些球的形状、大小、质地等完全相同,在看不到球的条件下,随机地从袋子中摸出三个球,下列事件是必然事件的是( )A、摸出的三个球中至少有一个球是黑球 B、摸出的三个球中至少有一个球是白球 C、摸出的三个球中至少有两个球是黑球 D、摸出的三个球中至少有两个球是白球3. 一元二次方程 的根的情况是A、有两个不相等的实数根 B、有两个相等的实数根 C、没有实数根 D、无法判断4. 如图,在 中, 所对的圆周角 ,若 为 上一点, ,则 的度数为( )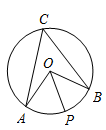 A、30° B、45° C、55° D、60°5. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、6. 二次函数 的图象如图所示,对称轴为直线 ,下列结论不正确的是( )
A、30° B、45° C、55° D、60°5. 用配方法解方程 ,变形后的结果正确的是( )A、 B、 C、 D、6. 二次函数 的图象如图所示,对称轴为直线 ,下列结论不正确的是( )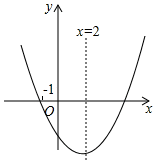 A、 B、当 时,顶点的坐标为 C、当 时, D、当 时,y随x的增大而增大7. 如图,将 绕点 逆时针旋转70°到 的位置,若 ,则 ( )
A、 B、当 时,顶点的坐标为 C、当 时, D、当 时,y随x的增大而增大7. 如图,将 绕点 逆时针旋转70°到 的位置,若 ,则 ( ) A、45° B、40° C、35° D、30°8. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( )
A、45° B、40° C、35° D、30°8. 如图,AB是⊙O的直径,弦CD⊥AB于点E,OC=5cm,CD=8cm,则AE=( ) A、8cm B、5cm C、3cm D、2cm9. 国家实施”精准扶贫“政策以来,很多贫困人口走向了致富的道路.某地区2016年底有贫困人口9万人,通过社会各界的努力,2018年底贫困人口减少至1万人.设2016年底至2018年底该地区贫困人口的年平均下降率为 ,根据题意列方程得( )A、 B、 C、 D、10. 如图等边△ABC的边长为4cm,点P,点Q同时从点A出发点,Q沿AC以1cm/s的速度向点C运动,点P沿A﹣B﹣C以2cm/s的速度也向点C运动,直到到达点C时停止运动,若△APQ的面积为S(cm2),点Q的运动时间为t(s),则下列最能反映S与t之间大致图象是( )
A、8cm B、5cm C、3cm D、2cm9. 国家实施”精准扶贫“政策以来,很多贫困人口走向了致富的道路.某地区2016年底有贫困人口9万人,通过社会各界的努力,2018年底贫困人口减少至1万人.设2016年底至2018年底该地区贫困人口的年平均下降率为 ,根据题意列方程得( )A、 B、 C、 D、10. 如图等边△ABC的边长为4cm,点P,点Q同时从点A出发点,Q沿AC以1cm/s的速度向点C运动,点P沿A﹣B﹣C以2cm/s的速度也向点C运动,直到到达点C时停止运动,若△APQ的面积为S(cm2),点Q的运动时间为t(s),则下列最能反映S与t之间大致图象是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 编号为2,3,4,5,6的乒乓球放在不透明的袋内,从中任抽一个球,抽中编号是偶数的概率是.12. 关于x的一元二次方程(a﹣1)x2+x+|a|﹣1=0的一个根是0,则实数a的值为.13. 若一个圆锥的底面圆的周长是 cm,母线长是 ,则该圆锥的侧面展开图的圆心角度数是 .14. 如图,在矩形 中, . 若将 绕点 旋转后,点 落在 延长线上的点 处,点 经过的路径为 ,则图中阴影部分的面积为.
 15. 如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为 ,则AK= .
15. 如图,正方形ABCD绕点B逆时针旋转30°后得到正方形BEFG,EF与AD相交于点H,延长DA交GF于点K.若正方形ABCD边长为 ,则AK= .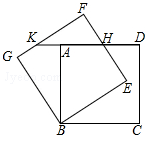 16. 二次函数 中的自变量 与函数值 的部分对应值如下表:
16. 二次函数 中的自变量 与函数值 的部分对应值如下表:…
…
…
…
则 的解为.
三、解答题
-
17. 解方程:3x(x﹣2)=x﹣2.
18. 已知:在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(5,4),B(0,3),C(2,1).
( 1 )画出△ABC关于原点成中心对称的△A1B1C1 , 并写出点C1的坐标;
( 2 )画出将A1B1C1绕点C1按顺时针旋转90°所得的△A2B2C1.
19. 有4张看上去无差别的卡片,上面分别写着1,2,3,4.(1)、一次性随机抽取2张卡片,求这两张卡片上的数字之和为奇数的概率;(2)、随机摸取1张后,放回并混在一起,再随机抽取1张,求两次取出的卡片上的数字之和等于4的概率.20. 将一块面积为 的矩形菜地的长减少 ,它就变成了正方形,求原菜地的长.21. 如图,在 中, ,以 为直径的 交 于 ,点 在线段 上,且 . (1)、求证: 是 的切线.(2)、若 ,求 的半径.
(1)、求证: 是 的切线.(2)、若 ,求 的半径.
