浙江省台州市椒江区2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2020-12-22 类型：期中考试

进入出卷网下载

一、选择题（本大题共10小题，每小题3分，共30分）

1. ﹣2的倒数是（　　）

A、﹣ $\frac{1}{2}$ B、﹣2 C、 $\frac{1}{2}$ D、2

查看试题解析
2. 用代数式表示：a的2倍与3的和．下列表示正确的是（）

A、2a﹣3 B、2a+3 C、2（a﹣3） D、2（a+3）

查看试题解析
3. 世界文化遗产长城总长约670000米，将数670000用科学记数法可表示为（）

A、6.7×10⁴ B、6.7×10⁵ C、6.7×10⁶ D、67×10⁴

查看试题解析
4. 下列计算正确的是（）

A、a+a＝a² B、6x³﹣5x²＝x C、3x²+2x³＝5x⁵ D、3a²b﹣4ba²＝﹣a²b

查看试题解析
5. 下列说法中，错误的是（）

A、单项式与多项式统称为整式 B、多项式3a+3b的系数是3 C、ab+2是二次二项式 D、单项式x²yz的系数是1

查看试题解析
6. 下列说法：①0是最小的整数；②最大的负整数是﹣1；③正有理数和负有理数统称有理数；④一个有理数的平方是正数.其中正确的有（）

A、1 个 B、2个 C、3个 D、4个

查看试题解析
7. 下列去括号正确的是（）

A、a+（b+c）＝a+b﹣c B、a +（b﹣c）＝a+b+c C、a﹣（b+c）＝a﹣b+c D、a﹣（b﹣c）＝a﹣b+c

查看试题解析
8. 已知ax＝ay，下列等式变形不一定成立的是（）

A、b+ax＝b+ay B、x＝y C、x﹣ax＝x﹣ay D、 $\frac{a x}{a^{2} + 1}$ ＝ $\frac{a y}{a^{2} + 1}$

查看试题解析
9. 如果a＞0，b＜0，a+b＜0，那么下列各式中大小关系正确的是（）

A、﹣b＜﹣a＜b＜a B、﹣a＜b＜a＜﹣b C、b＜﹣a＜﹣b＜a D、b＜﹣a＜a＜﹣b

查看试题解析
10.
A，B，C，D，E五个景点之间的路线如图所示．若每条路线的里程a(km)及行驶的平均速度b(km/h)用(a，b)表示，则从景点A到景点C用时最少的路线是（　　）

A、A⇒E⇒C B、A⇒B⇒C C、A⇒E⇒B⇒C D、A⇒B⇒E⇒C

查看试题解析

二、填空题（本大题共6小题，每小题4分，共24分）

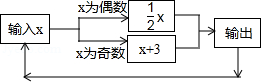
11. 某天最低气温是﹣1℃，最高气温比最低气温高9℃，则这天的最高气温是 ℃．

查看试题解析
12. 已知x＝3是关于x的方程2x﹣m＝7的解，则m的值是.

查看试题解析
13. 已知多项式 $x^{| m |}$ + (m - 2)x -10 是二次三项式，m 为常数，则 m 的值为.

查看试题解析
14. 若﹣x^my⁴与 $\frac{1}{12}$ x³yⁿ是同类项，则(m﹣n)⁹＝

查看试题解析
15. 已知y＝ax⁵+bx³+cx﹣5，当x＝﹣3时，y＝5，那么当x＝3时，y的值是.

查看试题解析
16. 如图所示的运算程序中，若开始输入的x值为36，我们发现第1次输出的结果为18，第2次输出的结果为9，…第2020次输出的结果为.

查看试题解析

三、解答题（本大题共8小题，共66分.解答应写出文字说明、证明过程或演算步骤）

17. 计算：

(1)、1.5÷ $\frac{5}{8}$ ×（﹣ $\frac{5}{4}$ ）+ | 3- π |

(2)、﹣1²﹣24×（﹣ $\frac{1}{6}$ + $\frac{2}{3}$ ﹣ $\frac{3}{4}$ ）

查看试题解析
18. 解方程：

(1)、x + 2 + 6x ＝ 3x﹣2；

(2)、 $\frac{1}{2}$ x﹣1＝ $\frac{3}{7} x$ .

查看试题解析
19. 有8筐白菜，以每筐25千克为标准，超过的千克数记作正数，不足的千克数记作负数，称后的纪录如下：

回答下列问题：

(1)、这8筐白菜中最接近标准重量的这筐白菜重千克；

(2)、这8筐白菜一共重多少千克？

查看试题解析
20. 先化简再求值： 4（ $\frac{1}{2}$ x²﹣3xy﹣y²）﹣3（x²﹣7xy﹣2y²），其中x，y满足（x+1）²+|y﹣2|＝0.

查看试题解析
21. 已知代数式A＝2x²+3xy+2y，B＝x²﹣xy+x．

(1)、求A﹣2B；

(2)、若A﹣2B的值与x的取值无关，求y的值．

查看试题解析
22. 下面是A市与B市出租车收费标准，A市为：行程不超过3千米收起步价10元，超过3千米后超过部分每千米收1.2元；B市为：行程不超过3千米收起步价8元，超过3千米后超过部分每千米收1.5元．

(1)、填空：在A市，某人乘坐出租车2千米，需车费元；

(2)、试求在A市与在B市乘坐出租车x（x＞3，x为整数）千米的车费分别为多少元？

(3)、计算在A市与在B市乘坐出租车5千米的车费的差．

查看试题解析
23. 定义：对任意一个两位数 $a$ ，如果 $a$ 满足个位数字与十位数字互不相同，且都不为零，那么称这个两位数为“迥异数”，将一个“迥异数”的个位数字与十位数字对调后得到一个新的两位数，把这个新两位数与原两位数的和与11的商记为 $f (a)$ ．例如： $a = 12$ ，对调个位数字与十位数字得到新两位数21，新两位数与原两位数的和为21+12=33，和与11的商为33÷11=3，所以 $f (12) = 3$ ．根据以上定义，回答下列问题：

(1)、填空：①下列两位数：40，42，44中，“迥异数”为；②计算： $f (23)$ =；

(2)、如果一个“迥异数” $b$ 的十位数字是 $k$ ，个位数字是 $2 (k + 1 ）$ ，且 $f (b) = 11$ ，请求出“迥异数” $b$ ．

查看试题解析
24. 已知多项式x³+2x²y﹣4的常数项是a，次数是b，若a、b两数在数轴上所对应的点为A、B.

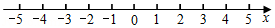(1)、线段AB的长＝；

(2)、数轴上在B点右边有一点C，点C到A、B两点的距离和为11，求点C在数轴上所对应的数；

(3)、若P、Q两点分别从A、B出发，数0为点O，同时沿数轴正方向运动，P点的速度是Q点速度的2倍，且3秒后，2OP＝OQ，求点Q运动的速度.

查看试题解析