浙江省绍兴市越城区2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-22 类型:期中考试
一、选择题(本题有10个小题,每小题4分,共40分)
-
1. 对于二次函数 的图象,下列说法正确的是( )A、开口向下 B、对称轴是x=﹣1 C、顶点坐标是(1,2) D、与x轴有两个交点2. 如图所示的圆规,点A是铁尖的端点,点B是铅笔芯尖的端点,点A与点B的距离是2 cm.若铁尖的端点A固定,铅笔芯尖的端点B绕点A旋转一周,则作出圆的直径是( )
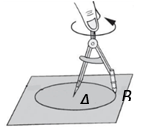 A、1 cm B、2 cm C、4 cm D、 cm3. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、154. 对于函数 ,使得 随 的增大而增大的 的取值范围是( )A、 B、 C、 D、5. 将抛物线 通过平移得到 ,则下列平移过程正确的是( )A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位 C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位6. 对于二次函数y=ax2+bx+c(a≠0),我们把使函数值等于0的实数x叫做这个函数的零点 , 则二次函数y=x2-mx-5(m为实数)的零点的个数是( )A、1 B、2 C、0 D、不能确定7. 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )
A、1 cm B、2 cm C、4 cm D、 cm3. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、154. 对于函数 ,使得 随 的增大而增大的 的取值范围是( )A、 B、 C、 D、5. 将抛物线 通过平移得到 ,则下列平移过程正确的是( )A、先向左平移2个单位,再向上平移3个单位 B、先向左平移2个单位,再向下平移3个单位 C、先向右平移2个单位,再向下平移3个单位 D、先向右平移2个单位,再向上平移3个单位6. 对于二次函数y=ax2+bx+c(a≠0),我们把使函数值等于0的实数x叫做这个函数的零点 , 则二次函数y=x2-mx-5(m为实数)的零点的个数是( )A、1 B、2 C、0 D、不能确定7. 如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是( )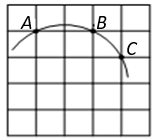 A、(0,0) B、(-1,1) C、(-1,0) D、(-1,-1)8. 某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水流呈抛物线状(抛物线所在平面与墙面垂直,如图).如果抛物线的最高点M离墙1米,离地面 米,则水流落地点B离墙距离是( )
A、(0,0) B、(-1,1) C、(-1,0) D、(-1,-1)8. 某幢建筑物,从10米高的窗口A用水管向外喷水,喷出的水流呈抛物线状(抛物线所在平面与墙面垂直,如图).如果抛物线的最高点M离墙1米,离地面 米,则水流落地点B离墙距离是( )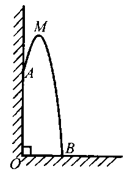 A、2米 B、3米 C、4米 D、5米9. 已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作弧PQ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交于弧PQ点M,N;(3)连接OM,MN. 根据以上作图过程及所作图形,下列结论中错误的是( )
A、2米 B、3米 C、4米 D、5米9. 已知锐角∠AOB如图,(1)在射线OA上取一点C,以点O为圆心,OC长为半径作弧PQ,交射线OB于点D,连接CD;(2)分别以点C,D为圆心,CD长为半径作弧,交于弧PQ点M,N;(3)连接OM,MN. 根据以上作图过程及所作图形,下列结论中错误的是( )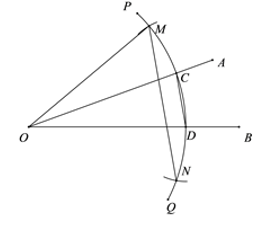 A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD10. 如图,一次函数y1=2x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣2)x+c的图象可能是( )
A、∠COM=∠COD B、若OM=MN,则∠AOB=20° C、MN∥CD D、MN=3CD10. 如图,一次函数y1=2x与二次函数y2=ax2+bx+c图象相交于P、Q两点,则函数y=ax2+(b﹣2)x+c的图象可能是( )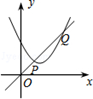 A、
A、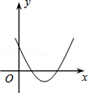 B、
B、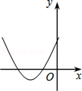 C、
C、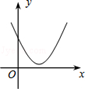 D、
D、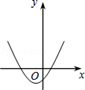
二、填空题(本题有6个小题,每小题5分,共30分)
-
11. 已知 ,则 =.12. 从甲地到乙地有A,B,C三条不同的公交线路.为了解早高峰期间这三条线路上的公交车从甲地到乙地的用时情况,在每条线路上随机选取了500个班次的公交车,收集了这些班次的公交车用时(单位:分钟)的数据,统计如下:

30≤t≤35
35<t≤40
40<t≤45
45<t≤50
合计
A
59
151
166
124
500
B
50
50
122
278
500
C
45
265
167
23
500
早高峰期间,乘坐(填“A”,“B”或“C”)线路上的公交车,从甲地到乙地“用时不超过45分钟”的可能性最大.
13. 如图,A,B,C,D为⊙O上的点,OC⊥AB于点E.若∠CDB=30°,OA=2,则AB的长为.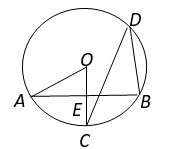 14. 如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣ (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .
14. 如图的一座拱桥,当水面宽AB为12m时,桥洞顶部离水面4m,已知桥洞的拱形是抛物线,以水平方向为x轴,建立平面直角坐标系,若选取点A为坐标原点时的抛物线解析式是y=﹣ (x﹣6)2+4,则选取点B为坐标原点时的抛物线解析式是 .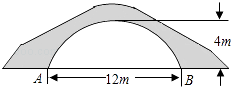 15. 如图所示,把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径为cm.
15. 如图所示,把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=4 cm,则球的半径为cm.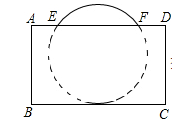 16. 如图,直线l: ,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3)…Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1 , 0),A2(x2 , 0),A3(x3 , 0)…,An+1(xn+1 , 0)(n为正整数),设x1=d(0<d<1)若其中一条抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则我们把这条抛物线就称为:“美丽抛物线”.则当d(0<d<1)的大小变化时能产生美丽抛物线相应的d的值是.
16. 如图,直线l: ,一组抛物线的顶点B1(1,y1),B2(2,y2),B3(3,y3)…Bn(n,yn)(n为正整数)依次是直线l上的点,这组抛物线与x轴正半轴的交点依次是:A1(x1 , 0),A2(x2 , 0),A3(x3 , 0)…,An+1(xn+1 , 0)(n为正整数),设x1=d(0<d<1)若其中一条抛物线的顶点与x轴的两个交点构成的三角形是直角三角形,则我们把这条抛物线就称为:“美丽抛物线”.则当d(0<d<1)的大小变化时能产生美丽抛物线相应的d的值是.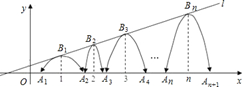
三、 解答题(本题有8个小题,共80分)
-
17. 已知抛物线的解析式为y= -3x2+6x+9.(1)、求它的对称轴;(2)、求它与x轴,y轴的交点坐标.18. 小强同学报名参加运动会,有以下5个项目可供选择:径赛项目:100m,200m,400m(分别用A1、A2、A3表示);田赛项目:跳远,跳高(分别用B1、B2表示).(1)、小强同学从5个项目中任选一个,恰好是田赛项目的概率为;(2)、小强同学从5个项目中任选两个,利用树状图或表格列举出所有可能出现的结果,并求恰好是一个田赛项目和一个径赛项目的概率.19. 如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.
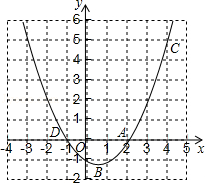 (1)、求二次函数的解析式;(2)、在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.20. 如图,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.
(1)、求二次函数的解析式;(2)、在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.20. 如图,已知点A,B的坐标分别为(0,0),(4,0),将△ABC绕点A按逆时针方向旋转90°得到△AB′C′.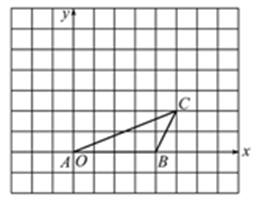 (1)、画出△AB′C′.(2)、写出点C′的坐标.(3)、求旋转过程中点B所经过的路径长.21. 某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:
(1)、画出△AB′C′.(2)、写出点C′的坐标.(3)、求旋转过程中点B所经过的路径长.21. 某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型;②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.
 (1)、如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;(2)、如果设计成圆弧型,求该圆弧所在圆的半径;(3)、在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.22. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.(1)、不妨设该种品牌玩具的销售单价在40元的基础上上涨x元(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
(1)、如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;(2)、如果设计成圆弧型,求该圆弧所在圆的半径;(3)、在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.22. 某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨2元,就会少售出20件玩具.(1)、不妨设该种品牌玩具的销售单价在40元的基础上上涨x元(x>0),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:销售单价(元)
x+40
销售量y(件)
销售玩具获得利润w(元)
(2)、在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价应定为多少元?(3)、在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?23. 我们知道:有一内角为直角的三角形叫做直角三角形.类似地,我们定义:有一内角为45°的三角形叫做半直角三角形.如图,在平面直角坐标系中,O为原点,A(4,0),B(﹣4,0),D是y轴上的一个动点,∠ADC=90°(A、D、C按顺时针方向排列),BC与经过A、B、D三点的⊙M交于点E,DE平分∠ADC,连结AE,BD.显然△DCE、△DEF、△DAE是半直角三角形.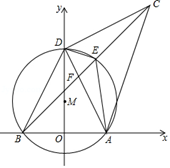 (1)、求证:△ABC是半直角三角形;(2)、求证:∠DEC=∠DEA;(3)、若点D的坐标为(0,8),求AE的长。24. 如图,已知二次函数y=x2+bx+c经过A,B两点,BC⊥x轴于点C,且点A(﹣1,0),C(4,0),AC=BC.
(1)、求证:△ABC是半直角三角形;(2)、求证:∠DEC=∠DEA;(3)、若点D的坐标为(0,8),求AE的长。24. 如图,已知二次函数y=x2+bx+c经过A,B两点,BC⊥x轴于点C,且点A(﹣1,0),C(4,0),AC=BC.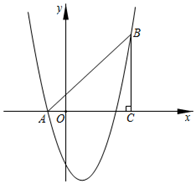 (1)、求抛物线的解析式;(2)、点E是线段AB上一动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段EF的长度最大时,求点E的坐标及S△ABF;(3)、点P是抛物线对称轴上的一个动点,是否存在这样的P点,使△ABP成为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、点E是线段AB上一动点(不与A,B重合),过点E作x轴的垂线,交抛物线于点F,当线段EF的长度最大时,求点E的坐标及S△ABF;(3)、点P是抛物线对称轴上的一个动点,是否存在这样的P点,使△ABP成为直角三角形?若存在,求出所有点P的坐标;若不存在,请说明理由.