浙江省宁波市镇海区蛟川书院2020届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-22 类型:期中考试
一、选择题(每小题4分,共40分)
-
1. 在 中,∠C=90°,sinA= ,则tanA=( )A、 B、 C、1 D、2. 圆O的半径为3,圆心O到直线的距离为4,则该直线与圆O的位置关系是( )A、相切 B、相交 C、相离 D、以上都不对3. 已知线段 =1, =4,线段 是线段 , 的比例中项,则线段 的长度是( )A、2 B、 C、16 D、4. 如图,PA,PB分别切⊙O于点A,B,PA=12,CD切⊙O于点E,交PA,PB于点C,D两点,则△PCD的周长是( )
 A、12 B、18 C、24 D、305. 下列说法中:⑴三点确定一个圆;⑵直径所对的圆周角是直角;⑶平分弦的直径垂直于弦,并且平分弦所对的弧;⑷相等的圆心角所对的弧相等;⑸圆内接四边形的对角互补.其中正确的个数为( )A、1个 B、2个 C、3个 D、4个6. 已知一个扇形的半径为R,圆心角为n°,当这个扇形的面积与一个直径为R的圆面积相等时,则n等于( )A、180 B、120 C、90 D、607. 如图,在△ABC中, , , ,点F为边BC上一点,则下列条件不能保证△FDB与△ADE相似的是( )
A、12 B、18 C、24 D、305. 下列说法中:⑴三点确定一个圆;⑵直径所对的圆周角是直角;⑶平分弦的直径垂直于弦,并且平分弦所对的弧;⑷相等的圆心角所对的弧相等;⑸圆内接四边形的对角互补.其中正确的个数为( )A、1个 B、2个 C、3个 D、4个6. 已知一个扇形的半径为R,圆心角为n°,当这个扇形的面积与一个直径为R的圆面积相等时,则n等于( )A、180 B、120 C、90 D、607. 如图,在△ABC中, , , ,点F为边BC上一点,则下列条件不能保证△FDB与△ADE相似的是( ) A、∠A=∠BFD B、DF//AC C、 D、8. 如图,在⊙O中,E是直径AB延长线上一点,CE切⊙O于点E,若CE=2BE,则∠E的余弦值为 ( )
A、∠A=∠BFD B、DF//AC C、 D、8. 如图,在⊙O中,E是直径AB延长线上一点,CE切⊙O于点E,若CE=2BE,则∠E的余弦值为 ( ) A、 B、 C、 D、9. 如图,△ABC和△CDE都是等边三角形,点G在CA的延长线上,GB=GE,若BE+CG=10, ,则AF的长为( )
A、 B、 C、 D、9. 如图,△ABC和△CDE都是等边三角形,点G在CA的延长线上,GB=GE,若BE+CG=10, ,则AF的长为( ) A、1 B、 C、 D、210. 如图,四个水平放置正方形的边长都为4,顶点A、B、C是圆上的点,则此圆的面积为( )
A、1 B、 C、 D、210. 如图,四个水平放置正方形的边长都为4,顶点A、B、C是圆上的点,则此圆的面积为( )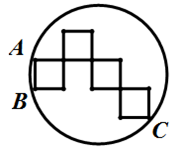 A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每小题5分,共30分)
-
11. 已知 ( 为锐角),满足方程 ,则 =.12. 如图,五边形ABCDE是⊙O的内接正五边形,AF是⊙O的直径,则∠BDF的度数是.
 13. 如图,AB是半圆O的直径,且AB=4,∠BAC=30°,则 的长为 .
13. 如图,AB是半圆O的直径,且AB=4,∠BAC=30°,则 的长为 . 14. 如图,点P是△ABC的重心,过P作AB的平行线DE,分别交AC,BC于点D,E.作DF//BC交AB于点F,若△ABC的面积为18,则四边形BEDF的面积为.
14. 如图,点P是△ABC的重心,过P作AB的平行线DE,分别交AC,BC于点D,E.作DF//BC交AB于点F,若△ABC的面积为18,则四边形BEDF的面积为.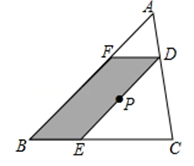 15. 如图,在锐角△ABC中,AB= ,BC=4,∠C=45°.若点D是AC边上的一点,将△BCD沿BD所在直线翻折得到△BDF,BF交AC于E,DF//AB,则AC= , DE=.
15. 如图,在锐角△ABC中,AB= ,BC=4,∠C=45°.若点D是AC边上的一点,将△BCD沿BD所在直线翻折得到△BDF,BF交AC于E,DF//AB,则AC= , DE=.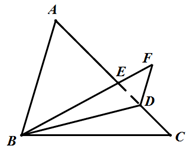 16. 如图,矩形ABCD中,AB=3,BC=4,点E是对角线AC上的动点,点F是边BC上的动点,点P是半径为1的⊙B上的动点, 则PE+EF的最小值为.
16. 如图,矩形ABCD中,AB=3,BC=4,点E是对角线AC上的动点,点F是边BC上的动点,点P是半径为1的⊙B上的动点, 则PE+EF的最小值为.
三、解答题(第17题6分,第18、19题各9分,第20—22题各10分,第23题12分,第24题14分,共80分)
-
17. 计算:18. 已知⊙O的半径为r=2,弦AB= ,点B是 的中点, AB与CD交于点E.
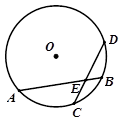 (1)、求圆心O到弦AB的距离;(2)、求∠AEC的度数.19. 如图,在边长为1的5×5的正方形网格上有两个三角形,它们顶点都在格点上.
(1)、求圆心O到弦AB的距离;(2)、求∠AEC的度数.19. 如图,在边长为1的5×5的正方形网格上有两个三角形,它们顶点都在格点上.

图1
(1)、△ABC与△DEF是否相似?请说明理由;(2)、请在空白网格上画出△MNP~△ABC,并指出相似比.△MNP~△ABC ,相似比为(要求△MNP三个顶点都在格点上,并与△ABC、△DEF都不全等)20. 如图,某学校体育场看台的顶端C到地面的垂直距离CD为2m,看台所在斜坡CM的坡比i=1:3,在点C处测得旗杆顶点A的仰角为30°,在点M处测得旗杆顶点A的仰角为60°,且B,M,D三点在同一水平线上.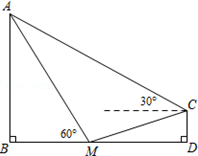 (1)、求DM的长.(2)、求旗杆AB的高度.(结果保留根号)21. 如图,有一座拱桥是圆弧形,它的跨度AB=60m,拱高PD=18m.
(1)、求DM的长.(2)、求旗杆AB的高度.(结果保留根号)21. 如图,有一座拱桥是圆弧形,它的跨度AB=60m,拱高PD=18m.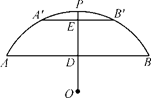 (1)、求圆弧所在的圆的半径r的长.(2)、当洪水泛滥到跨度只有30m时,要采取紧急措施,若拱顶离水面只有4m,即PE=4m时,是否要采取紧急措施?22. 如图,在边长为5的菱形OABC中,sin∠AOC= ,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题:
(1)、求圆弧所在的圆的半径r的长.(2)、当洪水泛滥到跨度只有30m时,要采取紧急措施,若拱顶离水面只有4m,即PE=4m时,是否要采取紧急措施?22. 如图,在边长为5的菱形OABC中,sin∠AOC= ,O为坐标原点,A点在x轴的正半轴上,B,C两点都在第一象限.点P以每秒1个单位的速度沿O→A→B→C→O运动一周,设运动时间为t(秒).请解答下列问题: 备用图(1)、当CP⊥OA时,求t的值;(2)、以点P为圆心,以OP为半径画圆,当⊙P与菱形OABC的一边所在直线相切,且切点不在菱形的边上时,求出t的值.23. 定义:若一个四边形能被其中一条对角线分割成两个相似三角形,则称这个四边形为“友爱四边形”,这条对角线叫“友爱线”.
备用图(1)、当CP⊥OA时,求t的值;(2)、以点P为圆心,以OP为半径画圆,当⊙P与菱形OABC的一边所在直线相切,且切点不在菱形的边上时,求出t的值.23. 定义:若一个四边形能被其中一条对角线分割成两个相似三角形,则称这个四边形为“友爱四边形”,这条对角线叫“友爱线”. (1)、如图1,在4×4的正方形网格中,有一个网格Rt△ABC和两个网格四边形ABCD与四边形ABCE,其中是被AC分割成的“友爱四边形”的是 ;(2)、如图2,四边形ABCD是“友爱四边形”,对角线AC是“友爱线”,同时也是∠BCD的角平分线,若△ABC中,AB=2,BC=3,AC=4,求友爱四边形ABCD的周长;(3)、如图3,在△ABC中,AB≠BC,∠ABC=60°,△ABC的面积为 ,点D是∠ABC的平分线上一点,连接AD,CD.若四边形ABCD是被BD分割成的“友爱四边形”,求BD的长.24. 如图,△ABC内接于⊙O,AB是直径,CD⊥AB于D,P为AB延长线上一点,∠BCP=∠BCD.
(1)、如图1,在4×4的正方形网格中,有一个网格Rt△ABC和两个网格四边形ABCD与四边形ABCE,其中是被AC分割成的“友爱四边形”的是 ;(2)、如图2,四边形ABCD是“友爱四边形”,对角线AC是“友爱线”,同时也是∠BCD的角平分线,若△ABC中,AB=2,BC=3,AC=4,求友爱四边形ABCD的周长;(3)、如图3,在△ABC中,AB≠BC,∠ABC=60°,△ABC的面积为 ,点D是∠ABC的平分线上一点,连接AD,CD.若四边形ABCD是被BD分割成的“友爱四边形”,求BD的长.24. 如图,△ABC内接于⊙O,AB是直径,CD⊥AB于D,P为AB延长线上一点,∠BCP=∠BCD. (1)、求证:PC是⊙O的切线;(2)、点E是⊙O上一点,∠ACE=2∠BCP,延长CD交BE于F,CF=10.
(1)、求证:PC是⊙O的切线;(2)、点E是⊙O上一点,∠ACE=2∠BCP,延长CD交BE于F,CF=10.①求CP的长;
②若BE=9,求⊙O的半径.