浙江省宁波市镇海区蛟川书院2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2020-12-22 类型:期中考试
一、选择题:本题共12小题,每小题4分,共48分。在每小题给出的四个选项中,只有一项符合题目要求的。
-
1. 下列“表情图”中,属于轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 如图△ABC,作BC边上的高,以下作法正确的是( )A、
2. 如图△ABC,作BC边上的高,以下作法正确的是( )A、 B、
B、 C、
C、 D、
D、 3. 已知点P1(a﹣1,5)和P2(3,b)关于x轴对称,则(a+b)2020的值为( )A、92020 B、0 C、1 D、320204. 已知m是整数,以4m+5、2m-1、20-m这三个数作为同一个三角形三边的长,则满足条件的三角形个数有( )A、0个 B、1个 C、2个 D、无数个5. 若直线y=kx+b是由直线y=2x+4沿x轴向右平移4个单位所得,则k,b的值分别是( )A、k=﹣2,b=4 B、k=2,b=8 C、k=2,b=﹣4 D、k=2,b=06. 下列命题是真命题的有( )
3. 已知点P1(a﹣1,5)和P2(3,b)关于x轴对称,则(a+b)2020的值为( )A、92020 B、0 C、1 D、320204. 已知m是整数,以4m+5、2m-1、20-m这三个数作为同一个三角形三边的长,则满足条件的三角形个数有( )A、0个 B、1个 C、2个 D、无数个5. 若直线y=kx+b是由直线y=2x+4沿x轴向右平移4个单位所得,则k,b的值分别是( )A、k=﹣2,b=4 B、k=2,b=8 C、k=2,b=﹣4 D、k=2,b=06. 下列命题是真命题的有( )①若a>b,则a2>b2;②如果直角三角形两条边的长度分别为3和4,那么斜边上中线的长度为2.5;③若一个三角形一边的中线等于这边的一半,那么这个三角形是直角三角形;④点(3,4)关于y轴对称点的坐标为(-3,4);⑤等腰三角形的两条边长分别为3和7,则三角形的周长是13或17.
A、1 B、2 C、3 D、47. 有一直角三角形纸片,∠C=90°,BC=6,AC=8,现将△ABC按如图那样折叠,使点A与点B重合,折痕为DE,则CE的长为( ) A、 B、 C、 D、48. 某老师出门散步时离家的距离y与时间x之间的函数图象如图所示,若用黑点表示某老师家的位置,则某老师散步行走的路线可能是( )
A、 B、 C、 D、48. 某老师出门散步时离家的距离y与时间x之间的函数图象如图所示,若用黑点表示某老师家的位置,则某老师散步行走的路线可能是( ) A、
A、 B、
B、 C、
C、 D、
D、 9. 一次函数 分别与x,y轴相交于A,B两点,在坐标轴上取一点C,使得 为等腰三角形,这样的点C有( )个.A、7 B、8 C、9 D、1010. 已知关于 的不等式组 的解集中任意一个 的值均不在 的范围内,则 的取值范围是( )A、 或 B、 或 C、 D、11. 如图,在平面直角坐标系中,点A1、A2、A3…An在x轴上,B1、B2、B3…Bn在直线y= x上,若A1(1,0),且△A1B1A2、△A2B2A3…△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1、S2、S3、…、Sn.则S2020可表示为( )
9. 一次函数 分别与x,y轴相交于A,B两点,在坐标轴上取一点C,使得 为等腰三角形,这样的点C有( )个.A、7 B、8 C、9 D、1010. 已知关于 的不等式组 的解集中任意一个 的值均不在 的范围内,则 的取值范围是( )A、 或 B、 或 C、 D、11. 如图,在平面直角坐标系中,点A1、A2、A3…An在x轴上,B1、B2、B3…Bn在直线y= x上,若A1(1,0),且△A1B1A2、△A2B2A3…△AnBnAn+1都是等边三角形,从左到右的小三角形(阴影部分)的面积分别记为S1、S2、S3、…、Sn.则S2020可表示为( ) A、24037 B、24038 C、24039 D、2404012. 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连结DM 、 MC下列结论:①DF=DN;②△ABM≌△BNM;③△CMN是等腰三角形;④AE=CN;其中正确的结论个数是( )
A、24037 B、24038 C、24039 D、2404012. 如图,等腰Rt△ABC中,∠BAC=90°,AD⊥BC于D,∠ABC的平分线分别交AC、AD于E、F两点,M为EF的中点,延长AM交BC于点N,连结DM 、 MC下列结论:①DF=DN;②△ABM≌△BNM;③△CMN是等腰三角形;④AE=CN;其中正确的结论个数是( )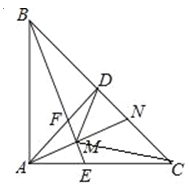 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题:本题共6小题,每小题4分,共24分。
-
13. 写一个经过点(-1,0),且y随x增大而增大的一次函数.14. 如图,在Rt△ABC中,∠ABC=90°,AB=BC= ,△ABC≌△MNC,若∠ACM= 60°,连结BM,则BM的长是.
 15. 有长度分别为1,2,3,4,5,6,7,8,9,10(cm)的木棒各一根,利用它们(允许连接加长,但不许折断)能围成周长不同的等边三角形共有种.16. 无论m取什么实数,点P(3m-2,m+4)都在直线 上,若Q( )是直线 上的点,则 的值为.17. 如图,七个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线将这七个正方形分成面积相等的两部分,则该直线的解析式为.
15. 有长度分别为1,2,3,4,5,6,7,8,9,10(cm)的木棒各一根,利用它们(允许连接加长,但不许折断)能围成周长不同的等边三角形共有种.16. 无论m取什么实数,点P(3m-2,m+4)都在直线 上,若Q( )是直线 上的点,则 的值为.17. 如图,七个边长为1的正方形如图摆放在平面直角坐标系中,经过P点的一条直线将这七个正方形分成面积相等的两部分,则该直线的解析式为. 18. 如图所示:已知直线 : 交x轴于点A,交y轴于点 B.直线 经过点B且与x轴交于点C(2 , 0)在直线 上取一点M,使得M到 的 距离为2.则M点的坐标为.
18. 如图所示:已知直线 : 交x轴于点A,交y轴于点 B.直线 经过点B且与x轴交于点C(2 , 0)在直线 上取一点M,使得M到 的 距离为2.则M点的坐标为.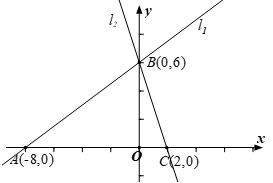
三、解答题:第19题6分,第20-21题各8分,第22-24题各10分,第25题12分,第26题14分,共78分。
-
19. 解下列不等式组(1)、(2)、20. 如图,△ABC中,AB=BC,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF
 (1)、求证:△ABE≌△CBF;
(1)、求证:△ABE≌△CBF;
(2)、若∠CAE=35°,求∠ACF的度数.
21. 如图,小明的爸爸在鱼池边开了一块四边形土地种了一些蔬菜,爸爸让小明计算一下土地的面积,以便计算一下产量.小明找了一卷米尺,测得AB=4 米,BC=3米,CD=13米,DA=12米,又已知∠B=90°,那么这块土地的面积 为多少? 22. 台球运动中,如果母球P击中桌边点A,经桌边反弹击中相邻的另一桌边,再次反弹,那么母球P经过的路线BC与PA平行吗?请你把台球母球P的完整路线P-A-B-C画出来,并作出适当的标注或说明.
22. 台球运动中,如果母球P击中桌边点A,经桌边反弹击中相邻的另一桌边,再次反弹,那么母球P经过的路线BC与PA平行吗?请你把台球母球P的完整路线P-A-B-C画出来,并作出适当的标注或说明.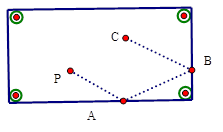
 23. 一医疗用品厂用于生产的全部劳力为450个工时,原料为400个单位,生产一盒试纸要使用15个工时、20个单位的原料,售价为80元;生产一盒口罩要使用10个工时、5个单位的原料,售价为45元.在劳力和原料的限制下合理安排生产试纸、口罩的盒数,可以使试纸和口罩总售价尽可能高.请你用你所学过的数学知识分析,总售价是否可能达到2200元?24. 用[x]表示不大于x的最大整数,如[2.1]=2,[-4.5]=-5,已知x1 ,x2是方程6x+7=3[x]的解,且x1<x2 , 点A(x1 , y1)和B (x2 , y2)是直线y=-2x-1上的两点,试比较y1与y2+l的大小。25. 如图,在平面直角坐标系中,直线经过点A ( ,0)点 B(o, ).
23. 一医疗用品厂用于生产的全部劳力为450个工时,原料为400个单位,生产一盒试纸要使用15个工时、20个单位的原料,售价为80元;生产一盒口罩要使用10个工时、5个单位的原料,售价为45元.在劳力和原料的限制下合理安排生产试纸、口罩的盒数,可以使试纸和口罩总售价尽可能高.请你用你所学过的数学知识分析,总售价是否可能达到2200元?24. 用[x]表示不大于x的最大整数,如[2.1]=2,[-4.5]=-5,已知x1 ,x2是方程6x+7=3[x]的解,且x1<x2 , 点A(x1 , y1)和B (x2 , y2)是直线y=-2x-1上的两点,试比较y1与y2+l的大小。25. 如图,在平面直角坐标系中,直线经过点A ( ,0)点 B(o, ). (1)、求直线l的函数解析式﹔(2)、若给定点 M (5,0 ),存在直线止的两点 P ,Q,使得以 o ,P ,Q为顶点的三角形与△O M P全等,请求出所有符合条件的点的坐标﹒26. 如图
(1)、求直线l的函数解析式﹔(2)、若给定点 M (5,0 ),存在直线止的两点 P ,Q,使得以 o ,P ,Q为顶点的三角形与△O M P全等,请求出所有符合条件的点的坐标﹒26. 如图 (1)、如图1,已知△ABC是正三角形,点E直线BC的下方,BPC为钝角,且满足∠APB=∠ACB,求证:PA=PC+PB;(2)、如图2,已知△ABC是等腰直角三角形,∠ABC=90°点p在直线BC的下方,∠BPC为钝角,仍满足∠APB=∠ACB,求证:PA=PC+ PB;(3)、探究,若△ABC仍是等腰三角形,∠ABC= 120°其他条件不变,问PA,PB,PC三者又有何数量关系,并给予证明.
(1)、如图1,已知△ABC是正三角形,点E直线BC的下方,BPC为钝角,且满足∠APB=∠ACB,求证:PA=PC+PB;(2)、如图2,已知△ABC是等腰直角三角形,∠ABC=90°点p在直线BC的下方,∠BPC为钝角,仍满足∠APB=∠ACB,求证:PA=PC+ PB;(3)、探究,若△ABC仍是等腰三角形,∠ABC= 120°其他条件不变,问PA,PB,PC三者又有何数量关系,并给予证明.