陕西省渭南韩城市2020-2021学年七年级上学期数学期中考试试卷

试卷更新日期：2020-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 单项式 $- 4 a b^{2}$ 的系数为（）

A、-1 B、-4 C、1 D、4

查看试题解析
2. 据科学家统计，目前地球上已经被定义、命名的生物约有1000万种左右，数字1000万用科学记数法表示为（）

A、1×10³ B、1×10⁶ C、1×10⁷ D、10×10⁶

查看试题解析
3. $- \frac{3}{5}$ 的4次幂应记成（）

A、 $- \frac{3^{4}}{5}$ B、 $- {\frac{3}{5}}^{4}$ C、 $\frac{{(- 3)}^{4}}{5}$ D、 ${(- \frac{3}{5})}^{4}$

查看试题解析
4. 下列各组中的两项，属于同类项的是（　　）

A、a²与a B、﹣3ab与2ab C、a²b与ab² D、a与b

查看试题解析
5. 计算下列各式，结果为负数的是（）

A、(-7)÷(-8) B、(-7)×(-8) C、(-7)-(-8) D、(-7)+(-8)

查看试题解析
6. 若 $a + 2 b = 3$ ，则多项式 $2 a + 4 b - 1$ 的值为（）

A、3 B、4 C、5 D、6

查看试题解析
7. 如图，数轴上的点 $C$ 对应的数为 $c$ ，则数轴上与数 $- 2 c$ 对应的点可能是（）

A、点 $E$ B、点 $D$ C、点 $B$ D、点 $A$

查看试题解析
8. 把一张厚度为 $0.1 m m$ 的白纸连续对折5次后的厚度为（）

A、 $0.5 m m$ B、 $1 m m$ C、 $1.6 m m$ D、 $3.2 m m$

查看试题解析
9. 按如图所示的运算程序，能使输出m的值为1的是（）

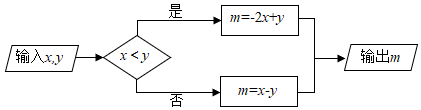A、x＝1，y＝1 B、x＝2，y＝0 C、x＝1，y＝2 D、x＝3，y＝2

查看试题解析
10. 在数轴上，点 $A$ 、 $B$ 在原点 $O$ 的两侧，分别表示数 $a$ 、2，将点 $A$ 向右平移3个单位长度，得到点 $C$ ，若点 $C$ 与点 $O$ 的距离是点 $B$ 与点 $O$ 的距离的2倍，则 $a$ 的值为（）

A、-1 B、-7 C、1或 -7 D、7或 -1

查看试题解析

二、填空题

11. 由四舍五入法，将数0.6942精确到十分位，所得的近似值是.

查看试题解析
12. 将多项式 $a b^{3} - 2 a^{2} b - 3 a^{3} b^{2} - 1$ 按照 $b$ 的指数从小到大的顺序排列为.

查看试题解析
13. 已知 $m$ 是 $4$ 的相反数， $n$ 比 $m$ 的相反数小2，则 $m - n$ 等于.

查看试题解析
14. 按照一定规律排列的一列数依次是9，13，17，21，25，...，按照此规律，这列数中的第100个数是.

查看试题解析

三、解答题

15. 计算： $- 1^{4} + | 2 - {(- 3)}^{2} | + \frac{3}{2} \div (- \frac{1}{2})$

查看试题解析
16. 已知多项式 $- \frac{1}{3} x^{3} y^{m} + \frac{1}{2} x y^{2} - 3 x^{3} + 6$ 是六次四项式，单项式 $3 x^{n} y^{2}$ 的次数与这个多项式的次数相同，求 $m + n$ 的值

查看试题解析
17. 某城市某天早上7点的气温为 $- 7 ° C$ ，上午10点的气温为 $- 2 ° C$ ，中午12点的气温为 $1 ° C$ ，下午2点的气温为 $4 ° C$

(1)、求这四个时刻的平均气温

(2)、求该城市早上 $7$ 点与下午2点的温差

查看试题解析
18. 已知数轴上点 $A$ 表示的数-1比6大，点 $B$ 、 $C$ 表示互为相反数的两个数，且点 $C$ 与点 $A$ 间的距离为2，求 $B$ 、 $C$ 表示的数

查看试题解析
19. 先化简，再求值： $5 a b - 2 [3 a b - (4 a b^{2} + \frac{1}{2} a b)] - 5 a b^{2}$ ，其中 $a = - \frac{1}{3}$ ， $b = 2$

查看试题解析
20. $a$ 是最大的负整数， $b$ 是最小的非负数，有理数 $c$ 的倒数的绝对值是 $\frac{1}{2}$ ，求的值 $- a + b^{3} - 2 c$

查看试题解析
21. 数学老师给出这样一个题目： $2 A + B = - x^{2} + 2 x$ ， $A = - 3 x^{2} - 2 x + 6$ ，求

(1)、 $B$ 的值

(2)、 $B - A$ 的值

查看试题解析
22. 一颗猕猴桃能提供一个人一日维生素 $C$ 需求量的两倍多，被誉为“水果之王”，现有30筐猕猴桃，以每筐20千克为标准，超过或不足的千克数分别用正、负数来表示，记录如下：

单位（千克）

-2

-1

0.5

0

1

1.5

筐数

2

4

4

5

5

10

(1)、与标准质量相比，30筐猕猴桃总计超过或不足多少千克？

(2)、若猕猴桃每千克售价5元，则这30筐猕猴桃可卖多少元？

查看试题解析
23. 笔记本的单价是x元，圆珠笔的单价是y元．小红买3本笔记本，6支圆珠笔；小明买6本笔记本，3支圆珠笔．

(1)、小红和小明买这些笔记本和圆珠笔一共花费多少元钱？

(2)、若每本笔记本比每支圆珠笔贵2元，求小明比小红多花费了多少元钱？

查看试题解析
24. 一个三位正整数 $M$ ，其各位数字均不为零且互不相等.若将 $M$ 的十位数字与百位数字交换位置，得到一个新的三位数，我们称这个三位数为 $M$ 的“友谊数”，如：168的“友谊数”为“618”：若从 $M$ 的百位数字、十位数字、个位数字中任选两个组成一个新的两位数，并将得到的所有两位数求和，我们称这个和为M的“团结数”，如：123的“团结数”为 $12 + 13 + 21 + 23 + 31 + 32 = 132$

(1)、若 $M$ 的其百位数字为 $a$ ，十位数字为 $b$ 、个位数字为 $c$ ，试说明M与其“友谊数”的差能被15整除；

(2)、若一个三位正整数 $N$ ，其百位数字为2，十位数字为 $a$ 、个位数字为 $b$ ，且各位数字互不相等 $(a \neq 0 ， b \neq 0)$ ，求 $N$ 的“团结数”

查看试题解析
25. 某出租车驾驶员从公司出发，在南北向的人民路上连续接送5批客人，行驶路程记录如下（规定向南为正，向北为负，单位：km）：

第1批

第2批

第3批

第4批

第5批

5km

2km

﹣4km

﹣3km

10km

(1)、接送完第5批客人后，该驾驶员在公司什么方向，距离公司多少千米？

(2)、若该出租车每千米耗油0.2升，那么在这过程中共耗油多少升？

(3)、若该出租车的计价标准为：行驶路程不超过3km收费10元，超过3km的部分按每千米加1.8元收费，在这过程中该驾驶员共收到车费多少元？

查看试题解析

单位（千克）	-2	-1	0.5	0	1	1.5
筐数	2	4	4	5	5	10

第1批	第2批	第3批	第4批	第5批
5km	2km	﹣4km	﹣3km	10km