浙江省温岭市团队六校2021届九年级上学期数学期中考试试卷

试卷更新日期：2020-12-22 类型：期中考试

进入出卷网下载

一、单选题

1. 下列标志图中，既是轴对称图形，又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 下列是一元二次方程的是（）

A、 $4 x^{2} + \frac{3}{x} + 2 = 0$ B、 $2 x^{2} - y - 1 = 0$ C、 $a x^{2} + b x + c = 0$ D、 $4 x^{2} + 3 x + 2 = 0$

查看试题解析
3. 抛物线y=x²－2x－3与y轴的交点的纵坐标为（）.

A、－3 B、－1 C、1 D、3

查看试题解析
4. 如图，⊙ $O$ 的弦 $A B = 8$ ， $M$ 是 $A B$ 的中点，且 $O M = 3$ ，则⊙ $O$ 的直径等于（）

A、8 B、2 C、10 D、5

查看试题解析
5. 如图，将 $R t △ A B C$ 绕点A按顺时针旋转一定角度得到 $R t △ A D E$ ，点B的对应点D恰好落在BC边上 $.$ 若 $A B = 1$ ， $∠ B = 60^{\circ}$ ，则CD的长为 $($ $)$

A、 $0.5$ B、 $1.5$ C、 $\sqrt{2}$ D、1

查看试题解析
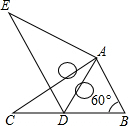6. 两年前生产1吨甲种药品的成本是5000元．随着生产技术的进步，成本逐年下降，第2年的年下降率是第1年的年下降率的2倍，现在生产1吨甲种药品成本是2400元．为求第一年的年下降率，假设第一年的年下降率为x，则可列方程（）

A、5000（1﹣x﹣2x）=2400 B、5000（1﹣x）²=2400 C、5000﹣x﹣2x=2400 D、5000（1﹣x）（1﹣2x）=2400

查看试题解析
7. 如图所示，边长为2的正方形 $A B C D$ 绕点 $A$ 逆时针旋转 $45 °$ 后得到正方形 $A B^{'} C^{'} D^{'}$ ，边 $B^{'} C^{'}$ 与 $C D$ 交于点 $O$ ，则四边形 $A B^{'} O D$ 的周长（）

A、 $2 \sqrt{2}$ B、 $4 \sqrt{2}$ C、 $2 + 2 \sqrt{2}$ D、4

查看试题解析
8. 过三点A（2，2），B（6，2），C（4，5）的圆的圆心坐标为（）

A、（4， $\frac{17}{6}$ ） B、（4，3） C、（5， $\frac{17}{6}$ ） D、（5，3）

查看试题解析
9. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，下列结论中正确的个数是（）

① $a c > 0$ ；② $a - b + c ⩽ 0$ ；③ $b^{2} - 4 a c < 0$ ；④ $2 c < 3 b$ ；⑤ $a + b > m (a m + b)$ （ $m$ 为实数，且 $m \neq 1$ ）

A、2个 B、3个 C、4个 D、5个

查看试题解析
10. 如图，在菱形 $A B C D$ 中， $∠ A = 60 °$ ， $A B = 3$ ， $⊙ A$ ， $⊙ B$ 的半径分别为2和1， $P$ ， $E$ ， $F$ 分别是 $C D$ 边、 $⊙ A$ 和 $⊙ B$ 上的动点，则 $P E + P F$ 的最小值是（）

A、 $3 \sqrt{3} - 3$ B、2 C、3 D、 $3 \sqrt{3}$

查看试题解析

二、填空题

11. 如图， $⊙ O$ 中， $O A ⊥ B C$ ， $∠ A O B = 46 °$ ，则 $∠ A D C =$ .

查看试题解析
12. 已知二次函数 $y = - x^{2} + 2 x + m$ 的部分图象如图所示，则关于 $x$ 的一元二次方程 $- x^{2} + 2 x + m = 0$ 的解为.

查看试题解析
13. 若点 $B (n + 3, 5)$ 与点 $A (4, m)$ 关于原点 $O$ 中心对称，则 $m + n =$ .

查看试题解析
14. 已知 $a$ ， $b$ 为一元二次方程 $x^{2} + 2 x + 9 = 0$ 的两根，那么 $a^{2} + a - b$ 的值为.

查看试题解析
15. 如图，点 $E$ 在正方形 $A B C D$ 的边 $C B$ 上，将 $△ D C E$ 绕点 $D$ 顺时针旋转90˚到 $△ A D F$ 的位置，连接 $E F$ ，过点 $D$ 作 $E F$ 的垂线，垂足为点 $H$ ，于 $A B$ 交于点 $G$ ，若 $A G = 4$ ， $B G = 3$ ，则 $B E$ 的长为.

查看试题解析
16. 如图，已知等边 $△ A B C$ 内接于 $⊙ O$ ， $A B = 4$ ，点 $D$ 为 $\overset{⌢}{A C}$ 上一点， $∠ A B D = 45 °$ ， $A E ⊥ B D$ 于点 $E$ ，则 $△ B D C$ 的周长是.

查看试题解析

三、解答题

17. 解方程：

(1)、 $x^{2} - 2 x = 5$

(2)、 ${(x - 2)}^{2} - 3 x + 6 = 0$

查看试题解析
18. 如图，在 $10 \times 10$ 的正方形网格纸，每个小正方形的边长为1个单位，将 $Δ A B C$ 向下平移4个单位，得到 $Δ A^{'} B^{'} C^{'}$ ，再把 $Δ A^{'} B^{'} C^{'}$ 绕点 $C^{'}$ 顺时针旋转 $90^{°}$ ，得到 $Δ {A^{'}}^{'} {B^{'}}^{'} {C^{'}}^{'}$ ，请你画出 $Δ A^{'} B^{'} C^{'}$ 和 $Δ {A^{'}}^{'} {B^{'}}^{'} {C^{'}}^{'}$ （不要求写画法）

查看试题解析
19. 如图，二次函数 $y = {(x + 2)}^{2} + m$ 的图象与 $y$ 轴交于点 $C$ ，点 $B$ 在抛物线上，且与点 $C$ 关于抛物线的对称轴对称.已知一次函数 $y = k x + b$ 的图象经过二次函数图象上的点 $A (- 1 ， 0)$ 及点 $B$ .

(1)、求二次函数的解析式

(2)、根据图象，写出满足 ${(x + 2)}^{2} + m \geq k x + b$ 的 $x$ 取值范围.

查看试题解析
20. 关于 $x$ 的一元二次方程 $x^{2} - (k + 3) x + 2 k + 2 = 0$ .

(1)、求证：方程总有两个实数根；

(2)、若方程有一根小于1，求 $k$ 的取值范围.

查看试题解析
21. 如图， $△ A B C$ 内接于 $⊙ O$ ， $A B$ 是 $⊙ O$ 的直径， $C$ 是 $\overset{⌢}{A D}$ 中点，弦 $C E ⊥ A B$ 于点 $H$ ，连结 $A D$ ，分别交 $C E$ 、 $B C$ 于点 $P$ 、 $Q$ ，连结 $B D$ .

(1)、求证： $P$ 是线段 $A Q$ 的中点；

(2)、若 $⊙ O$ 的半径为5， $D$ 是 $\overset{⌢}{B C}$ 的中点，求弦 $C E$ 的长.

查看试题解析
22. 如图，要在一面靠墙（墙长11米）的空地上，用长为16米的篱笆围成一个矩形花圃（靠墙一边不超过墙长），设与墙平行的一边 $B C$ 的长为 $x$ 米，面积为 $y$ 平方米.

(1)、直接写出：与墙垂直的一边 $A B$ 的长（用含 $x$ 的代数式表示）；

(2)、若矩形花圃的面积为30平方米，求 $B C$ 的长；

(3)、若与墙平行的一边 $B C$ 的长度不小于与墙垂直的一边 $A B$ 的长度，问 $B C$ 边应为多少米时，才能使矩形花圃 $A B C D$ 所占地面面积最小，最小的面积是多少？

查看试题解析
23. 问题解决
一节数学课上，老师提出了这样一个问题：如图1，点 $P$ 是等边 $△ A B C$ 内的一点， $P A = 6$ ， $P B = 8$ ， $P C = 10$ .你能求出 $∠ A P B$ 的度数和等边 $△ A B C$ 的面积吗？

小明通过观察、分析、思考，形成了如下思路：

如图1将 $△ B P C$ 绕点 $B$ 逆时针旋转60°，得到 $△ B P A$ ，连接 $P P^{'}$ ，可得 $△ B P P^{'}$ 是等边三角形，根据勾股定理逆定理可得 $A P^{'} P$ 是直角三角形，从而使问题得到解决.

(1)、结合小明的思路完成填空： $P P^{'} =$ ， $∠ A P P^{'} =$ ， $∠ A P B =$ ， $S_{△ A B C} =$ .

(2)、类比探究
Ⅰ如图2，若点 $P$ 是正方形 $A B C D$ 内一点， $P A = 1$ ， $P B = 2$ ， $P C = 3$ ，求 $∠ A P B$ 的度数和正方形的面积.

Ⅱ如图3，若点 $P$ 是正方形 $A B C D$ 外一点， $P A = 3$ ， $P B = 1$ ， $P C = \sqrt{11}$ ，求 $∠ A P B$ 的度数和正方形的面积.

查看试题解析
24. 在平面直角坐标系 $x O y$ 中，对于点 $P (a ， b)$ 和点 $Q (a ， b^{'})$ ，给出如下定义：若 $b^{'} = {\begin{matrix} b ， a \geq 1 \\ - b ， a < 1 \end{matrix}$ 则称点 $Q$ 为点 $P$ 的限变点.

(1)、点 $(2 ， 3)$ 的限变点的坐标是，点 $(- 2 ， 5)$ 的限变点的坐标是.

(2)、若点 $P$ 在函数 $y = - x + 3 (- 2 \leq x \leq k ， k > - 2)$ 的图象上，其限变点 $Q$ 的纵坐标 $b^{'}$ 的取值范围是 $- 5 \leq b^{'} \leq 2$ ，求 $k$ 的取值范围.

(3)、若点 $P$ 在关于 $x$ 的二次函数 $y = x^{2} - 2 t x + t^{2} + t$ 的图象上，其限变点 $Q$ 的纵坐标 $b^{'}$ 的取值范围是 $b^{'} \geq m$ 或 $b^{'} < n$ ，其中 $m > n$ 令 $s = m - n$ ，则 $s$ 关于 $t$ 的函数表达式及 $S$ 的取值范围.

查看试题解析