四川省资阳市资阳市雁江区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列计算正确的是（）

A、 $3 \sqrt{2}$ － $\sqrt{2}$ ＝3 B、 $\sqrt{6}$ + $\sqrt{6}$ ＝6 C、 $\sqrt{2}$ × $\sqrt{6}$ ＝2 $\sqrt{3}$ D、 $\sqrt{16}$ ÷ $\sqrt{4}$ ＝4

查看试题解析
2. 如图，在平面直角坐标系中，点 $A$ 的坐标为 $(4 ， 3)$ ，那么 $\sin α$ 的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{4}{5}$ D、 $\frac{3}{5}$

查看试题解析
3. 已知ab＜0，则 $\sqrt{- a^{2} b}$ 化简后为（）

A、 $- a \sqrt{- b}$ B、 $- a \sqrt{b}$ C、 $a \sqrt{b}$ D、 $a \sqrt{- b}$

查看试题解析
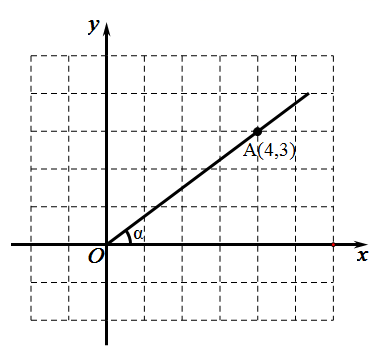4. 电影《我和我的祖国》讲述了普通人与国家之间息息相关的动人故事.一上映就获得全国人民的追捧，第一天票房约3亿元，以后每天票房按相同的增长率增长，三天后累计票房收入达10亿元，若把平均每天票房的增长率记作x，则可以列方程为（）

A、 $3 (1 + x) = 10$ B、 $3 {(1 + x)}^{2} = 10$ C、 $3 + 3 {(1 + x)}^{2} = 10$ D、 $3 + 3 (1 + x) + 3 {(1 + x)}^{2} = 10$

查看试题解析
5. 若方程2x² +x- 2m+1=0有一正实根和一负实根，则m的取值范围是（）

A、m≥ $\frac{7}{16}$ B、m ＞ $\frac{1}{2}$ C、m＞ $\frac{7}{16}$ D、m≥ $\frac{1}{2}$

查看试题解析
6. 已知线段AB的两个端点的坐标分别是A(m，m)， B(2n，n)，以原点O为位似中心，相似比为 $\frac{1}{2}$ ，把线段AB缩小，则经过位似变换后，A的对应点A^/的坐标是（）

A、( $\frac{1}{2}$ m， $\frac{1}{2}$ n) B、(- $\frac{1}{2}$ m，- $\frac{1}{2}$ n) C、( $\frac{1}{2}$ m， $\frac{1}{2}$ n) 或(- $\frac{1}{2}$ m，- $\frac{1}{2}$ n) D、(n， $\frac{1}{2}$ n) 或(-n，- $\frac{1}{2}$ n)

查看试题解析
7. 已知2+ $\sqrt{3}$ 是关于x的方程x² -4x+c=0的一个根，则方程的另一个根与c的值分别是（）

A、2－ $\sqrt{3}$ ，1 B、－6－ $\sqrt{3}$ ，15－8 $\sqrt{3}$ C、 $\sqrt{3}$ －2，-1 D、2－ $\sqrt{3}$ ，7+4 $\sqrt{3}$

查看试题解析
8. 如图所示图案是我国汉代数学家赵爽在注解《周髀算经》时给出的，人们称它为”赵爽弦图“．已知AE＝4，BE＝3，若向正方形ABCD内随意投掷飞镖（每次均落在正方形ABCD内，且落在正方形ABCD内任何一点的机会均等），则恰好落在正方形EFGH内的概率为（　　）

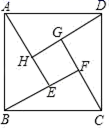A、 $\frac{1}{25}$ B、 $\frac{1}{16}$ C、 $\frac{1}{12}$ D、 $\frac{1}{9}$

查看试题解析
9. 将宽为2cm的长方形纸条折叠成如图所示的形状，那么折痕PQ的长是（）

A、 $\frac{2}{3} \sqrt{3}$ cm B、 $\frac{4}{3} \sqrt{3}$ cm C、 $\sqrt{5}$ cm D、2cm

查看试题解析
10. 如图，点A在线段BD上，在BD的同侧作等腰Rt△ABC和等腰Rt△ADE，其中∠ABC=∠AED=90°，CD与BE、AE分别交于点P、M.对于下列结论：①△CAM∽△DEM；②CD=2BE；③MP•MD=MA•ME；④2CB²=CP•CM.其中正确的是（）

A、①② B、①②③ C、①②③④ D、①③④

查看试题解析

二、填空题

11. 当x时， $\frac{\sqrt{x + 1}}{x - 2}$ 在实数范围内有意义.

查看试题解析
12. 若(x²+y²)²-2(x²+y²)-3=0，则x²+y²=.

查看试题解析
13. 在△ABC中BC=2，AB=2 $\sqrt{3}$ ，AC=b，且关于x的方程x²﹣4x+b=0有两个相等的实数根，则AC边上的中线长为．

查看试题解析
14. 如图，在△ABC中，点D、E分别在AB、AC上，∠ADE＝∠C ，如果AE＝4，△ADE的面积为5，四边形BCED的面积为15，那么AB的长为.

查看试题解析
15. 如图，在四边形ABCD中，点E ， F分别是AB ， AD的中点．若EF＝2，BC＝5，CD＝3，则tanC= ．

查看试题解析
16. 一组正方形按如图所示放置，其中顶点B₁在y轴上，顶点C₁ ， E₁ ， E₂ ， C₂ ， E₃ ， E₄ ， C₃…在x轴上．已知正方形A₁B₁C₁D₁的边长为1，∠B₁C₁O＝60°，B₁C₁∥B₂C₂∥B₃C₃ ，则正方形A₂₀₁₉B₂₀₁₉C₂₀₁₉D₂₀₁₉的边长是．

查看试题解析

三、解答题

17. 计算： ${(\frac{1}{2019})}^{- 1}$ +（3.14-π）⁰- $| \sqrt{2} - 2 \sqrt{3} |$ －2cos45 + $\sqrt{12}$ ．

查看试题解析
18. 解下列方程：

(1)、4x（1-x）=1；

(2)、2x²+6x-7=0（用配方法解）

查看试题解析
19. 如图，点C在△ADE的边DE上，AD与BC相交于点F，∠1=∠2， $\frac{AB}{AC} = \frac{AD}{AE}$ .

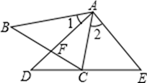(1)、试说明：△ABC ∽△ADE；

(2)、试说明：AF•DF=BF•CF.

查看试题解析
20. 有A、B两个黑布袋，A布袋中有四个除标号外完全相同的小球，小球上分别标有数字0，1，2，3，B布袋中有三个除标号外完全相同的小球，小球上分别标有数字0，1，2．小明先从A布袋中随机取出一个小球，用m表示取出的球上标有的数字，再从B布袋中随机取出一个小球，用n表示取出的球上标有的数字．

(1)、若用（m，n）表示小明取球时m与n 的对应值，用列表法(或画树状图)表示出（m，n）的所有取值；

(2)、求关于x的一元二次方程 $x^{2} - m x + \frac{1}{2} n = 0$ 有实数根的概率．

查看试题解析
21. 已知关于x的一元二次方程x²﹣（2k+1）x+4k﹣3＝0，

(1)、求证：无论k取什么实数值，该方程总有两个不相等的实数根？

(2)、当Rt△ABC的斜边a＝ $\sqrt{31}$ ，且两条直角边的长b和c恰好是这个方程的两个根时，求k的值．

查看试题解析
22. 小明同学上周末对公园钟楼(AB)的高度进行了测量，如图，他站在点D处测得钟楼顶部点A的仰角为67°，然后他从点D沿着坡度为i=1： $\frac{4}{3}$ 的斜坡DF方向走20米到达点F，此时测得建筑物顶部点A的仰角为45°.已知该同学的视线距地面高度为1.6米(即CD=EF=1.6米)，图中所有的点均在同一平面内，点B、D、G在同一条直线上，点E、F、G在同一条直线上，AB、CD、EF均垂直于BG.则钟楼AB的高约为? (精确到0.1) (参考数据： sin67°≈0.92，cos67°≈0.39，tan67°≈2.36)

查看试题解析
23. 某商场销售一批小家电，平均每天可售出20台，每台盈利40元．为了尽可能多的减少库存，商场决定采取适当的降价措施．经调查发现，在一定范围内，小家电的单价每降5元，商场平均每天可多售出10台．如果商场将这批小家电的单价降低x元，通过销售这批小家电每天盈利y元．

(1)、每天的销售量是台（用含x的代数式表示）；

(2)、求y与x之间的关系式；

(3)、如果商场通过销售这批小家电每天要盈利1050元，那么单价应降多少元？

查看试题解析
24. 如图，Rt△ABC中，∠BAC＝90°，AB＝2，AC＝4，D是BC边上一动点，G是BC边上的一动点，GE∥AD分别交AC、BA或其延长线于F、E两点

(1)、如图1，当BC＝5BD时，求证：EG⊥BC；

(2)、如图2，当BD＝CD时，FG+EG是否发生变化？证明你的结论；

(3)、当BD＝CD ， FG＝2EF时，DG的值＝．

查看试题解析