浙江省绍兴市柯桥区2021届九年级上学期数学期中考试试卷
试卷更新日期:2020-12-22 类型:期中考试
一、单选题
-
1. 已知 ,则 的值为( )A、 B、 C、 D、2. 如图,四边形 内接于 ,若 ,则 的大小为( )
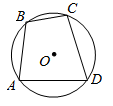 A、36° B、54° C、62° D、72°3. 函数图象 中,函数 与自变量 的部分对应值如表:
A、36° B、54° C、62° D、72°3. 函数图象 中,函数 与自变量 的部分对应值如表:…
-1
0
1
2
3
4
…
…
10
5
2
1
2
5
…
二次函数的对称轴是直线( ).
A、 B、 C、 D、4. 如图, 外接圆的圆心坐标是( )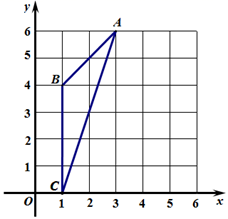 A、(5,2) B、(2,3) C、(1,4) D、(0,0)5. 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )
A、(5,2) B、(2,3) C、(1,4) D、(0,0)5. 如图,已知∠1=∠2,那么添加下列一个条件后,仍无法判定△ABC∽△ADE的是( )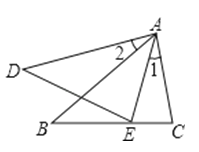 A、= B、= C、∠B=∠D D、∠C=∠AED6. 如图,若 绕点 按逆时针方向旋转 后能与 重合,则 ( ).
A、= B、= C、∠B=∠D D、∠C=∠AED6. 如图,若 绕点 按逆时针方向旋转 后能与 重合,则 ( ). A、 B、 C、 D、7. 如图, 过点B、C,圆心O在等腰 的内部, , , .则 的半径为( )
A、 B、 C、 D、7. 如图, 过点B、C,圆心O在等腰 的内部, , , .则 的半径为( ) A、5 B、 C、 D、8. 一条抛物线 的顶点为 , ,且与 轴有两个交点,其中一个交点是 ,则对 、 、 描述正确的是( ).A、 、 、 B、 、 、 C、 、 、 D、 、 、9. 如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA , 得到一个五角星图形和五边形MNFGH . 有下列3个结论:① AO⊥BE, ② ∠CGD=∠COD+∠CAD, ③ BM=MN=NE.其中正确的结论是( )
A、5 B、 C、 D、8. 一条抛物线 的顶点为 , ,且与 轴有两个交点,其中一个交点是 ,则对 、 、 描述正确的是( ).A、 、 、 B、 、 、 C、 、 、 D、 、 、9. 如图,A、B、C、D、E是⊙O上的5等分点,连接AC、CE、EB、BD、DA , 得到一个五角星图形和五边形MNFGH . 有下列3个结论:① AO⊥BE, ② ∠CGD=∠COD+∠CAD, ③ BM=MN=NE.其中正确的结论是( ) A、① ② B、① ③ C、② ③ D、① ② ③10. 如图,点 、 、 在直线 上,点 、 、 、 在直线 上,若 , 从如图所示的位置出发,沿直线 向右匀速运动,直到 与 重合.运动过程中 与矩形 重合部分的面积 随时间 变化的图象大致是( )
A、① ② B、① ③ C、② ③ D、① ② ③10. 如图,点 、 、 在直线 上,点 、 、 、 在直线 上,若 , 从如图所示的位置出发,沿直线 向右匀速运动,直到 与 重合.运动过程中 与矩形 重合部分的面积 随时间 变化的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 如图是用卡钳测量容器内径的示意图,现量得卡钳上 , 两个端点之间的距离为 , ,则容器的内径是.
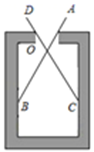 12. 如图, 、 、 是半径为3的 上的三点,已知 ,则劣弧 的长为.
12. 如图, 、 、 是半径为3的 上的三点,已知 ,则劣弧 的长为. 13. 如图,若被击打的小球飞行高度 (单位: )与飞行时间 (单位: )直接具有的关系为 ,则小球从飞出到落地所用的时间为s.
13. 如图,若被击打的小球飞行高度 (单位: )与飞行时间 (单位: )直接具有的关系为 ,则小球从飞出到落地所用的时间为s. 14. 如图, 的直角边 , , 在数轴上,在 上截取 ,以原点 为圆心, 为半径画弧,交数轴于点 ,则 的中点 对应的实数是.
14. 如图, 的直角边 , , 在数轴上,在 上截取 ,以原点 为圆心, 为半径画弧,交数轴于点 ,则 的中点 对应的实数是.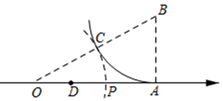 15. 如图,“ ”形纸片由八个边长为1的小正方形组成,过 点切一刀,刀痕是线段 ,若 下方部分的面积是纸片面积的一半,则 的长为.
15. 如图,“ ”形纸片由八个边长为1的小正方形组成,过 点切一刀,刀痕是线段 ,若 下方部分的面积是纸片面积的一半,则 的长为. 16. 如图,抛物线 与直线 交于 , 两点,将抛物线沿射线 方向平移 个单位.在整个平移过程中,抛物线与直线 交于点 ,则点 经过的路程为.
16. 如图,抛物线 与直线 交于 , 两点,将抛物线沿射线 方向平移 个单位.在整个平移过程中,抛物线与直线 交于点 ,则点 经过的路程为.
三、解答题
-
17. 筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图 ,点 表示筒车的一个盛水桶.如图 ,当筒车工作时,盛水桶的运行路径是以轴心 为圆心, 为半径的圆,且圆心在水面上方.若圆被水面截得的弦 长为 ,求筒车工作时,盛水桶在水面以下的最大深度.
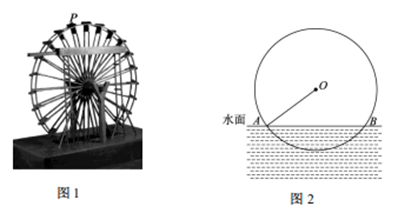 18. 如图,若二次函数 的图象与 轴交于 、 两点(点 在点 的左侧),与 轴交于 点.
18. 如图,若二次函数 的图象与 轴交于 、 两点(点 在点 的左侧),与 轴交于 点.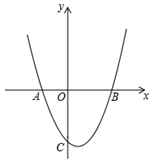 (1)、求 、 两点的坐标:(2)、若 为二次函数 图象上一点,求 的值.19. 如图,在△ABC中,BC=3,D为AC延长线上一点,AC=3CD , ∠CBD=∠A , 过D作DH∥AB , 交BC的延长线于点H .
(1)、求 、 两点的坐标:(2)、若 为二次函数 图象上一点,求 的值.19. 如图,在△ABC中,BC=3,D为AC延长线上一点,AC=3CD , ∠CBD=∠A , 过D作DH∥AB , 交BC的延长线于点H .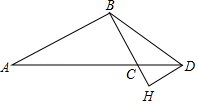 (1)、求证:△HCD∽△HDB .(2)、求DH长度.20. 如图,点C在以AB为直径的半圆⊙O上,AC=BC.以B为圆心,以BC的长为半径画圆弧交AB于点D.
(1)、求证:△HCD∽△HDB .(2)、求DH长度.20. 如图,点C在以AB为直径的半圆⊙O上,AC=BC.以B为圆心,以BC的长为半径画圆弧交AB于点D.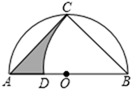 (1)、求∠ABC的度数;(2)、若AB=2,求阴影部分的面积.21. 研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半,如图,已知四边形 内接于 ,对角线 ,且
(1)、求∠ABC的度数;(2)、若AB=2,求阴影部分的面积.21. 研究发现:当四边形的对角线互相垂直时,该四边形的面积等于对角线乘积的一半,如图,已知四边形 内接于 ,对角线 ,且 (1)、求证: .(2)、若 的半径为8,弧 的度数为120°,求四边形 的面积.22. 随着国内疫情基本得到控制,旅游业也慢慢复苏,经市场调研发现旅游景点未来 天内,旅游人数y与时间x的关系如下表;每张门票z与时间x之间存在如下图所示的一次函数关系.( ,且x为整数)
(1)、求证: .(2)、若 的半径为8,弧 的度数为120°,求四边形 的面积.22. 随着国内疫情基本得到控制,旅游业也慢慢复苏,经市场调研发现旅游景点未来 天内,旅游人数y与时间x的关系如下表;每张门票z与时间x之间存在如下图所示的一次函数关系.( ,且x为整数)时间x(天)
1
4
7
10
人数y(人)
310
340
370
400

请结合上述信息解决下列问题:
(1)、直接写出:y关于x的函数关系式是.z与时间x函数关系式是.(2)、请预测未来 天中哪一天的门票收入最多,最多是多少?(3)、为支援武汉抗疫,该旅游景点决定从每天获得的门票收入中拿出 元捐赠给武汉红十字会,求捐款后共有几天每天剩余门票收入不低于12960元?23. 将边长为4的正方形 与边长为5的正方形 按图1位置放置, 与 在同一条直线上, 与 在同一条直线上.将正方形 绕点 逆时针旋转一周,直线 与直线 交于点 , (1)、 与 的数量关系:; 与 的位置关系:.(2)、如图2,当点 在线段 上时,求 的面积.(3)、连结 ,当 时,求 的值.24. 已知抛物线 经过点 , ,与 轴的另一个交点为 .
(1)、 与 的数量关系:; 与 的位置关系:.(2)、如图2,当点 在线段 上时,求 的面积.(3)、连结 ,当 时,求 的值.24. 已知抛物线 经过点 , ,与 轴的另一个交点为 .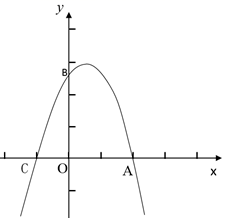

 (1)、求出此抛物线的表达式及点 坐标(2)、如图1, 的中点记为 , ,将 绕点 在 的左侧旋转, 与射线 交于点 , 与射线 交于点 .设 , ,求 关于 的函数关系式.(3)、当 的边经过点 时,求 , 的值(直接写出结果).
(1)、求出此抛物线的表达式及点 坐标(2)、如图1, 的中点记为 , ,将 绕点 在 的左侧旋转, 与射线 交于点 , 与射线 交于点 .设 , ,求 关于 的函数关系式.(3)、当 的边经过点 时,求 , 的值(直接写出结果).