四川省宜宾市叙州区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. 二次根式 中,x的取值范围是( )A、 B、 C、 D、2. 在一个不透明的盒子中有大小均匀的黄球与白球共12个,若从盒子中随机取出一个球,若取出的球是白球的概率是 ,则盒子中白球的个数是( ).A、3 B、4 C、6 D、83. 已知 是一元二次方程 的一个根,则m等于( )A、 B、1 C、 D、24. 如图,为了测量池塘边A,B两地之间的距离,在线段AB的同侧取一点C,连结CA并延长至点D,连结CB并延长至点E,使得A,B分别是CD,CE的中点,若DE=18m,则线段AB的长度是( )
 A、9m B、12m C、8m D、10m5. 将 以点O为位似中心放大为原来的2倍,得到 ,则 等于( )A、 B、 C、 D、6. 在 中, , , ,则直角边 的长是( )A、 B、 C、 D、7. 下列二次根式能与 合并的是( )A、 B、 C、 D、8. 如图,为了测量路灯离地面的高度,身高 的小明站在距离路灯的底部(点O) 的点A处,测得自己的影子 的长为 ,则路灯 的高度是( )
A、9m B、12m C、8m D、10m5. 将 以点O为位似中心放大为原来的2倍,得到 ,则 等于( )A、 B、 C、 D、6. 在 中, , , ,则直角边 的长是( )A、 B、 C、 D、7. 下列二次根式能与 合并的是( )A、 B、 C、 D、8. 如图,为了测量路灯离地面的高度,身高 的小明站在距离路灯的底部(点O) 的点A处,测得自己的影子 的长为 ,则路灯 的高度是( ) A、 B、 C、 D、9. 如图,正方形 的边长是4,E是 的中点,连接 、 相交于点O,则 的长是( )
A、 B、 C、 D、9. 如图,正方形 的边长是4,E是 的中点,连接 、 相交于点O,则 的长是( )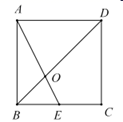 A、 B、 C、 D、510. 已知关于x的一元二次方程 的两个根分别是 , ,且满足 ,则m的值是( )A、0 B、 C、0或 D、 或011. 在 中, , 、 的对边分别是a、b,且满足 ,则 等于( )A、 B、2 C、 D、12. 如图,在平面直角坐标系 中,直线 与x轴、y轴分别交于点A、B,点C是y轴正半轴上的一点,当 时,则点C的纵坐标是( )
A、 B、 C、 D、510. 已知关于x的一元二次方程 的两个根分别是 , ,且满足 ,则m的值是( )A、0 B、 C、0或 D、 或011. 在 中, , 、 的对边分别是a、b,且满足 ,则 等于( )A、 B、2 C、 D、12. 如图,在平面直角坐标系 中,直线 与x轴、y轴分别交于点A、B,点C是y轴正半轴上的一点,当 时,则点C的纵坐标是( ) A、2 B、 C、 D、
A、2 B、 C、 D、二、填空题
-
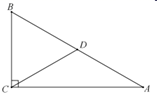
13. 计算: = .14. “蜀南竹海位于宜宾市境内”是事件;(填“确定”或“随机”)15. 如图,在 中, , , ,点D是斜边 的中点,则 ;
 16. 如图,某试验小组要在长50米,宽39米的矩形试验田中间开辟一横一纵两条等宽的小道,使剩余的面积是1800平方米,求小道的宽.若设小道的宽为x米,则所列出的方程是(只列方程,不求解)
16. 如图,某试验小组要在长50米,宽39米的矩形试验田中间开辟一横一纵两条等宽的小道,使剩余的面积是1800平方米,求小道的宽.若设小道的宽为x米,则所列出的方程是(只列方程,不求解) 17. 如图,在 中, , 于点 , , ,则 ;
17. 如图,在 中, , 于点 , , ,则 ;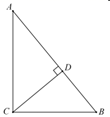 18. 如图,在 中, , ,延长 至点 ,使 ,则 .
18. 如图,在 中, , ,延长 至点 ,使 ,则 .
三、解答题
-
19. 解方程: .20. 若 的整数部分为x,小数部分为y;(1)、直接写出 , ;(2)、计算 的值.21. 已知关于 的方程 ;(1)、当 为何值时,方程有两个不相等的实数根;(2)、若 为满足(1)的最小正整数,求此时方程的两个根 , .22. 为了配合全市“创建全国文明城市”活动,某校共1200名学生参加了学校组织的创建全国文明城市知识竞赛,拟评出四名一等奖.(1)、求每一位同学获得一等奖的概率;(2)、学校对本次竞赛获奖情况进行了统计,其中七、八年级分别有一名同学获得一等奖,九年级有2名同学获得一等奖,现从获得一等奖的同学中任选两人参加全市决赛,请通过列表或画树状图的方法,求所选出的两人中既有七年级又有九年级同学的概率.23. 如图,为了测量山脚到塔顶的高度(即 的长),某同学在山脚A处用测角仪测得塔顶D的仰角为 ,再沿坡度为 的小山坡前进400米到达点B,在B处测得塔顶D的仰角为 .
 (1)、求坡面 的铅垂高度(即 的长);(2)、求 的长.(结果保留根号,测角仪的高度忽略不计).
(1)、求坡面 的铅垂高度(即 的长);(2)、求 的长.(结果保留根号,测角仪的高度忽略不计).