四川省攀枝花市米易县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\frac{\sqrt{x + 1}}{x}$ 有意义，则 $x$ 的取值范围是（）

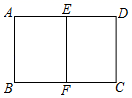
A、 $x \geq - 1$ B、 $x > - 1$ 且 $x \neq 0$ C、 $x \neq 0$ D、 $x \geq - 1$ 且 $x \neq 0$

查看试题解析
2. 下列计算错误的是（）

A、 $\sqrt{{(- 2)}^{2}} = - 2$ B、 $\sqrt{{(- 2)}^{2}} = 2$ C、 ${(- \sqrt{2})}^{2} = 2$ D、 $\sqrt{2^{2}} = 2$

查看试题解析
3. 下列根式是最简二次根式的是 $($ 　　 $)$

A、 $\frac{1}{\sqrt{2}}$ B、 $\sqrt{50}$ C、 $\sqrt{\frac{2}{7}}$ D、 $\sqrt{22}$

查看试题解析
4. 下列说法中，正确的是（）

A、被开方数不同的二次根式一定不是同类二次根式； B、只有被开方数完全相同的二次根式才是同类二次根式； C、 $3 \sqrt{5}$ 和 $\sqrt{15}$ 是同类二次根式； D、 $\frac{1}{2} \sqrt{12}$ 和 $\sqrt{\frac{1}{3}}$ 是同类二次根式.

查看试题解析
5. 如图，E ， F分别为矩形ABCD的边AD ， BC的中点，若矩形ABCD与矩形EABF相似，AB＝1，则矩形ABCD的面积是（）

A、4 B、2 C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
6. 如图：已知AB＝10，点C、D在线段AB上且AC＝DB＝2；P是线段CD上的动点，分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB，连接EF，设EF的中点为G；当点P从点C运动到点D时，则点G移动路径的长是（）

A、5 B、4 C、3 D、0

查看试题解析
7. 如图，矩形EFGO的两边在坐标轴上，点O为平面直角坐标系的原点，以y轴上的某一点为位似中心，作位似图形ABCD，且点B，F的坐标分别为（﹣4，4），（2，1），则位似中心的坐标为（　　）

A、（0，3） B、（0，2.5） C、（0，2） D、（0，1.5）

查看试题解析
8. 不透明的口袋内装有红球和白球和黄球共20个，这些球除颜色外其它都相同，将口袋内的球充分搅拌均匀，从中随机摸出一个球，记下颜色后放回，不断重复该摸球过程，共摸取2020次球，发现有505次摸到白球，则口袋中白球的个数是（　　）

A、5 B、10 C、15 D、20

查看试题解析
9. 已知 $a$ 是方程 $2 x^{2} - 4 x - 3 = 0$ 的一个根，则代数式 $2 a^{2} - 4 a$ 的值等于（）

A、3 B、2 C、0 D、1

查看试题解析
10. 如图，直线a∥b∥c，直线m、n与这三条平行线分别交于点A、B、C和点D、E、F．若AB＝3，BC＝5，DF＝12，则DE的值为（）

A、 $\frac{9}{4}$ B、4 C、 $\frac{9}{2}$ D、 $\frac{15}{2}$

查看试题解析

二、填空题

11. 已知实数a在数轴上的位置如图所示，则化简 $| a - 1 | - \sqrt{{(a + 1)}^{2}} =$ ．

查看试题解析
12. 阅读下列材料，我们知道 $(\sqrt{13} + 3) (\sqrt{13} - 3) = 4$ ，因此将 $\frac{8}{\sqrt{13} - 3}$ 的分子分母同时乘以“ $\sqrt{13} + 3$ ”，分母就变成了4，即 $\frac{8}{\sqrt{13} - 3} = \frac{8 (\sqrt{13} + 3)}{(\sqrt{13} - 3) (\sqrt{13} + 3)} = \frac{8 (\sqrt{13} + 3)}{4}$ ，从而可以达到对根式化简的目的，根据上述阅读材料解决问题：若 $m = \frac{2017}{\sqrt{2018} + 1}$ ，则代数式m⁵＋2m⁴﹣2017m³＋2016的值是．

查看试题解析
13. 当 $x =$ 时， $\sqrt{2 x - 4}$ 的值最小.

查看试题解析
14. 某农科所在相同条件下做玉米种子发芽实验，结果如下：

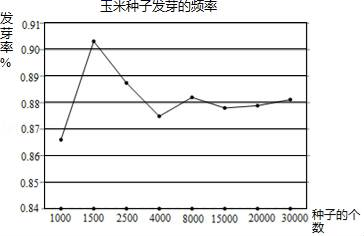
某位顾客购进这种玉米种子10千克，那么大约有千克种子能发芽．

查看试题解析
15. 一个直角三角形的两直角边长分别为 $\sqrt{12} c m$ 和 $\sqrt{8} c m$ ，则这个直角三角形的面积是cm² ．

查看试题解析
16. △ABC中，∠C=90°，tanA= $\frac{4}{3}$ ，则sinA+cosA= ．

查看试题解析

三、解答题

17. 计算： $2019^{0} - {(\frac{1}{2})}^{- 2} + \frac{1}{2} \times \sqrt{12} + | \sqrt{3} - 2 |$ ．

查看试题解析
18. 用配方法解方程：﹣3x²＋2x＋1＝0．

查看试题解析
19. 如图，若 $△ A_{1} B_{1} C_{1}$ 是由ABC平移后得到的，且 $△ ABC$ 中任意一点 $P (x ， y)$ 经过平移后的对应点为 $P_{1} (x - 5 ， y + 2)$

(1)、求点 $A_{1} ， B_{1} ， C_{1}$ 的坐标。

(2)、求 $△ A_{1} B_{1} C_{1}$ 的面积。

查看试题解析
20. 为了测量山坡上的电线杆PQ的高度，某数学活动小组的同学们带上自制的测倾器和皮尺来到山脚下，他们在A处测得信号塔顶端P的仰角是45°，信号塔底端点Q的仰角为30°，沿水平地面向前走100米到B处，测得信号塔顶端P的仰角是60°，求信号塔PQ得高度．

查看试题解析
21. 为了了解班级学生数学课前预习的具体情况，郑老师对本班部分学生进行了为期一个月的跟踪调查，他将调查结果分为四类：A：很好；B：较好；C：一般；D：不达标，并将调查结果绘制成以下两幅不完整的统计图，请你根据统计图解答下列问题：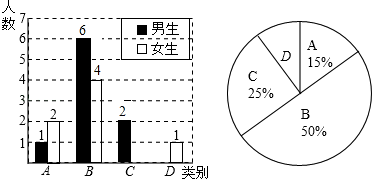

(1)、C类女生有名，D类男生有名，将上面条形统计图补充完整；

(2)、扇形统计图中“课前预习不达标”对应的圆心角度数是；

(3)、为了共同进步，郑老师想从被调查的A类和D类学生中各随机机抽取一位同学进行“一帮一”互助学习，请用画树状图或列表的方法求出所选两位同学恰好是一男一女同学的概率，

查看试题解析
22. 如图，在△ABC中，CD⊥AB，DE⊥AC，DF⊥BC，垂足分别为D，E，F．

(1)、求证：CE•CA＝CF•CB；

(2)、EF交CD于点O，求证：△COE∽△FOD；

查看试题解析
23. 为缓解交通压力，市郊某地正在修建地铁站，拟同步修建地下停车库．如图是停车库坡道入口的设计图，其中MN是水平线，MN∥AD，AD⊥DE，CF⊥AB，垂足分别为D，F，坡道AB的坡度＝1：3，AD＝9米，点C在DE上，CD＝0.5米，CD是限高标志牌的高度（标志牌上写有：限高米）．如果进入该车库车辆的高度不能超过线段CF的长，则该停车库限高多少米？（结果精确到0.1米，参考数据： $\sqrt{2}$ ≈1.41， $\sqrt{3}$ ≈1.73， $\sqrt{10}$ ≈3.16）

查看试题解析
24. 如图，在矩形ABCD中，AB=12cm，BC=6cm，点P沿AB边从点A开始向点B以2cm/s的速度移动，点Q沿DA边从点D开始向点A以1cm/s的速度移动，如果P、Q同时出发，用t（s）表示移动的时间（0≤t≤6），那么：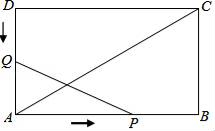

(1)、当t为何值时，△QAP是等腰直角三角形？

(2)、当t为何值时，以点Q、A、P为顶点的三角形与△ABC相似？

查看试题解析