浙江省慈溪市第四区域2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期:2020-12-22 类型:期中考试
一、单选题
-
1. 下列图形中,不是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 已知直角三角形一个锐角的度数为 ,则它的另一个内角(锐角)的度数为( )A、 B、 C、 D、3. 下列语句中,是定义的是( )A、两点确定一条直线 B、在同一平面内,不相交的两条直线叫做平行线 C、三角形的角平分线是一条线段 D、同角的余角相等4. 已知三角形的一边长为8,则它的另两边长分别可以是( )A、2,9 B、17,29 C、3,12 D、4,45. 下列命题中,其逆命题是真命题的是( )A、对顶角相等 B、两直线平行,同位角相等 C、全等三角形的对应角相等 D、如果 ,那么6. 下列条件中,能判断一个三角形是直角三角形的是( )A、三边长为 , , B、三条边 , , 满足关系 C、三条边的比是 D、三个角的比是7. 下列 与 不一定全等的是( )A、 , , B、 , , C、 , , D、 , ,8. 已知,在等腰 中,一个外角的度数为 ,则 的度数不能取的是( )A、 B、 C、 D、9. 如图, 为 平分线 上一点, , 的面积为12,则点 到直线 的距离为( )
2. 已知直角三角形一个锐角的度数为 ,则它的另一个内角(锐角)的度数为( )A、 B、 C、 D、3. 下列语句中,是定义的是( )A、两点确定一条直线 B、在同一平面内,不相交的两条直线叫做平行线 C、三角形的角平分线是一条线段 D、同角的余角相等4. 已知三角形的一边长为8,则它的另两边长分别可以是( )A、2,9 B、17,29 C、3,12 D、4,45. 下列命题中,其逆命题是真命题的是( )A、对顶角相等 B、两直线平行,同位角相等 C、全等三角形的对应角相等 D、如果 ,那么6. 下列条件中,能判断一个三角形是直角三角形的是( )A、三边长为 , , B、三条边 , , 满足关系 C、三条边的比是 D、三个角的比是7. 下列 与 不一定全等的是( )A、 , , B、 , , C、 , , D、 , ,8. 已知,在等腰 中,一个外角的度数为 ,则 的度数不能取的是( )A、 B、 C、 D、9. 如图, 为 平分线 上一点, , 的面积为12,则点 到直线 的距离为( )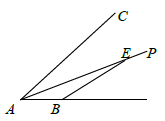 A、3 B、4 C、5 D、610. 如图,在 中, ,据尺规作图的痕迹判断以下结论错误的是( )
A、3 B、4 C、5 D、610. 如图,在 中, ,据尺规作图的痕迹判断以下结论错误的是( )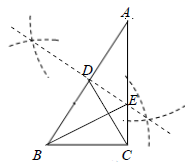 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
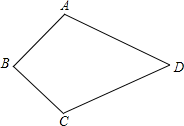
11. 写出一个能说明命题“如果 ,则 且 ”是假命题的反例:.12. 如图,在 和 中, , , ,则 .
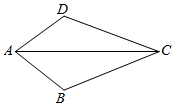 13. 如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A的度数为 .
13. 如图,∠ACD是△ABC的外角,若∠ACD=110°,∠B=50°,则∠A的度数为 .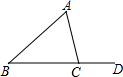 14. “三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任何一个角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=78°,则∠AOB等于度.
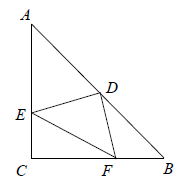
14. “三等分角”大约是在公元前五世纪由古希腊人提出来的.借助如图所示的“三等分角仪”能三等分任何一个角.这个三等分角仪由两根有槽的棒OA,OB组成,两根棒在O点相连并可绕O转动,C点固定,OC=CD=DE,点D,E可在槽中滑动,若∠BDE=78°,则∠AOB等于度.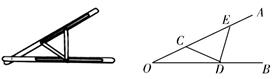 15. 如图,等腰三角形纸片 中, , 是 的平分线,放入一张等边三角形纸片 , 在 上, 在 上.若 , ,则等边 的边长为.
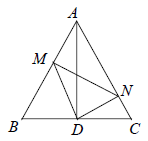
15. 如图,等腰三角形纸片 中, , 是 的平分线,放入一张等边三角形纸片 , 在 上, 在 上.若 , ,则等边 的边长为.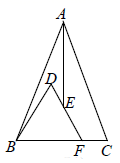 16. 如图,在 中, , , 为 的中点, ,垂足为 ,若 ,则 .
16. 如图,在 中, , , 为 的中点, ,垂足为 ,若 ,则 .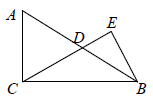
三、解答题
-
17. 如图,在 的网格中, , , 均为格点(最小正方形的顶点).在图1、图2中分别画一个与 成轴对称的格点三角形,所画的两个三角形的位置不同.
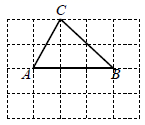
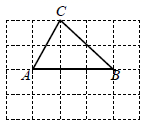
图1 图2
18. 已知线段 , .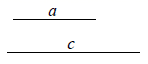 (1)、用尺规作一个 ,使 , , .(2)、在(1)中所画的 中,若 , ,求 的长.19. 如图,在 中, , 是高线,两条角平分线 和 交于点 .
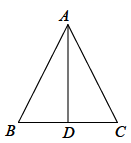
(1)、用尺规作一个 ,使 , , .(2)、在(1)中所画的 中,若 , ,求 的长.19. 如图,在 中, , 是高线,两条角平分线 和 交于点 .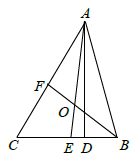 (1)、求 的度数.(2)、若 度( ),用含 的代数式表示 的度数.20. 证明:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.21. 已知:如图,AB=BC,∠A=∠C.求证:AD=CD.
(1)、求 的度数.(2)、若 度( ),用含 的代数式表示 的度数.20. 证明:如果一个三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.21. 已知:如图,AB=BC,∠A=∠C.求证:AD=CD.