四川省达州市渠县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 用配方法解方程x²-4x+3＝0时，原方程应变形为（）

A、(x+1)²＝1 B、(x-1)²＝1 C、(x+2)²＝1 D、(x-2)²＝1

查看试题解析
2. 下列几何体中，同一个几何体的主视图与左视图不同的是（）

A、 B、 C、 D、

查看试题解析
3. 若函数y＝ $\frac{m － 2}{x}$ 的图象在其象限内y的值随x的增大而增大，则m的取值范围是（）

A、m>2 B、m＜2 C、m>-2 D、m＜-2

查看试题解析
4. 如图，在△ABC中，DE//BC， $\frac{A D}{D B} ＝ \frac{1}{2}$ ，S_梯形_BCED＝8，则S_△_ABC是（）

A、13 B、12 C、10 D、9

查看试题解析
5. 如图，在菱形ABCD中，AB=5，对角线AC=6.若过点A作AE⊥BC，垂足为E，则AE的长为（）

A、4 B、2.4 C、4.8 D、5

查看试题解析
6. 下列一元二次方程中有两个不相等的实数根的方程是（）

A、(x+2)²＝0 B、x²+3＝0 C、x²+2x-17＝0 D、x²+x+5＝0

查看试题解析
7. 如图，反比例函数y＝ $\frac{m}{x}$ 的图象与一次函数y＝kx+b的图象相交于点A，B，已知点A的坐标为(-2，1)，点B的纵坐标为-2，根据图象信息可得关于x的方程 $\frac{m}{x}$ ＝kx+b的解为（）

A、-2，1 B、1，1 C、-2，-2 D、无法确定

查看试题解析
8. 用圆中两个可以自由转动的转盘做“配紫色”游戏，分别转动两个转盘，若其中一个转出红色，另一个转出蓝色即可配成紫色，那么可配成紫色的概率是（）

A、 $\frac{1}{2}$ B、 $\frac{1}{4}$ C、 $\frac{5}{12}$ D、 $\frac{7}{12}$

查看试题解析
9. 如图，四边形ABCD是矩形，点E在线段CB的延长线上，连接DE交AB于点F，∠AED＝2∠CED，点G为DF的中点．若BE＝1，AG＝3，则AB的长是（）

A、 $\sqrt{10}$ B、2 $\sqrt{2}$ C、 $\sqrt{11}$ D、 $2 \sqrt{3}$

查看试题解析
10. 如图，点M为反比例函数y＝ $\frac{1}{x}$ 上的一点，过点M作x轴，y轴的垂线，分别交直线y＝-x+b于C，D两点，若直线y＝-x+b分别与x轴，y轴相交于点A，B，则AD·BC的值是（）

A、3 B、2 $\sqrt{2}$ C、2 D、 $\sqrt{5}$

查看试题解析

二、填空题

11. 在四边形ABCD中，AD＝BC，AD∥BC．请你再添加一个条件，使四边形ABCD是菱形．你添加的条件是． (写出一种即可)

查看试题解析
12. 若 $\frac{b}{a}$ ＝ $\frac{1}{4}$ ，则 $\frac{a + b}{a － b}$ 的值是．

查看试题解析
13. 已知等腰三角形的两边长是方程x²﹣9x+18=0的两个根，则该等腰三角形的周长为.

查看试题解析
14. 将一副三角尺按如图所示的方式叠放在一起，边AC与BD相交于点E，则 $\frac{A E}{E C}$ 的值等于．

查看试题解析
15. 如图，已知A(1，y₁)，B(2，y₂)为反比例函数y＝ $\frac{2}{x}$ 图象上的两点，一个动点P(x，0)在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是．

查看试题解析
16. 在一只不透明的口袋中放入只有颜色不同的白色球3个，黑色球5个，黄色球n个，搅匀后随机从中摸取一个恰好是白色球的概率为 $\frac{1}{5}$ ，则放入的黄色球数n＝．

查看试题解析

三、解答题

17. 解方程：

(1)、3x(x-2)=4(x-2);

(2)、2x²-4x+1=0

查看试题解析
18. 根据要求画出下列立体图形的视图．

查看试题解析
19. 如图，ABCD是边长为1的正方形，在它的左侧补一个矩形ABFE，使得新矩形CEFD与矩形ABEF相似，求BE的长．

查看试题解析
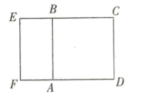20. 已知：如图，在平面直角坐标系xOy中，直线AB与x轴交于点A（-2，0），与反比例函数在第一象限内的图象交于点B（2，n），连接BO，若 $S_{△ A O B} = 4$ ．

(1)、求该反比例函数的解析式和直线AB的解析式；

(2)、若直线AB与y轴的交点为C，求 $△ O C B$ 的面积．

(3)、在第一象限内，求当一次函数值大于反比例函数值时的反比例函数值取值范围．

查看试题解析
21. 在如图所示的网格图中，已知 $△ A B C$ 和点 $M (1 ， 2)$

(1)、在网格图中点M为位似中心，画出 $△ A^{'} B^{'} C^{'}$ ，使其与 $△ A B C$ 的位似比为1：2．

(2)、写出 $△ A^{'} B^{'} C^{'}$ 的各顶点的坐标．

查看试题解析
22. 一家公司招考员工，每位考生要在A、B、C、D、E这5道试题中随机抽出2道题回答，规定答对其中1题即为合格．已知某位考生会答A、B两题，试求这位考生合格的概率．

查看试题解析
23. 某便民超市把一批进价为每件12元的商品，以每件定价20元销售，每天能够售出240件．经过调查发现：如果每件涨价1元，那么每天就少售20件；如果每件降价1元，那么每天能够多售出40件．

(1)、如果降价，那么每件要降价多少元才能使销售盈利达到1960元?

(2)、如果涨价，那么每件要涨价多少元才能使销售盈利达到1980元?

查看试题解析
24. 请阅读下面材料：
问题：已知方程x²+x-3＝0，求一个一元二次方程，使它的根分别是已知方程根的一半．

解：设所求方程的根为y，y= $\frac{x}{2}$ ，所以x＝2y

把x＝2y代入已知方程，得(2y)²+2y-3＝0

化简，得4y²+2y-3＝0

故所求方程为4y²+2y-3＝0

这种利用方程根的代换求新方程的方法，我们称为“换根法”．请用阅读材料提供的“换根法”解决下列问题：

(1)、已知方程2x²-x-15＝0，求一个关于y的一元二次方程，使它的根是已知方程根的相反数，则所求方程为：．

(2)、已知方程ax²+bx+c＝0(a≠0)有两个不相等的实数根，求一个关于y的一元二次方程，使它的根比已知方程根的相反数的一半多2．

查看试题解析
25. 已知四边形ABCD中，E，F分别是AB，AD边上的点，DE与CF相交于点G．

(1)、如图①，若四边形ABCD是矩形，且DE⊥CF，求证： $\frac{D E}{C F} ＝ \frac{A D}{C D}$ ．

(2)、如图②，若四边形ABCD是平行四边形，要使 $\frac{D E}{C F} ＝ \frac{A D}{C D}$ 成立，完成下列探究过程：
要使 $\frac{D E}{C F} ＝ \frac{A D}{C D}$ ，转化成 $\frac{D E}{A D} ＝ \frac{C F}{C D}$ ，显然△DEA与△CFD不相似，考虑 $\frac{D E}{A D} ＝ \frac{D F}{G D}$ ，需要△DEA∽△DFG，只需∠A＝∠；另一方面，只要 $\frac{C F}{C D} ＝ \frac{D F}{G D}$ ，需要△CFD∽△CDG，只需∠CGD＝∠ ．由此探究出使 $\frac{D E}{C F} ＝ \frac{A D}{C D}$ 成立时，∠B与∠EGC应该满足的关系是．

(3)、如图③，若AB＝BC＝6，AD＝CD=8，∠BAD=90°，DE⊥CF，那么 $\frac{D E}{C F}$ 的值是多少?(直接写出结果)

查看试题解析