云南省昆明市十县区2020-2021学年八年级上学期数学期中考试试卷
试卷更新日期：2020-12-22 类型：期中考试
一、单选题
-
1. 自新冠肺炎疫情发生以来，全国人民共同抗疫，各地积极普及科学防控知识，下面是科学防控知识的图片，图片上有图案和文字说明，其中图案是轴对称图形的是（ ）A、
打喷嚏 捂口鼻
B、
喷嚏后 慎揉眼
C、
勤洗手 勤通风
D、
戴口罩 讲卫生
2. 以下列各组线段为边（单位：cm），能组成三角形的是（ ）A、1，2，4 B、4，6，8 C、5，6，12 D、2，3，53. 如图，已知∠ABC＝∠DCB，添加一个条件使△ABC≌△DCB，下列添加的条件不能使△ABC≌△DCB的是（ ）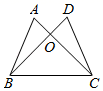
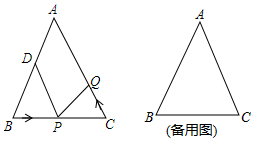
A、AC＝DB B、AB＝DC C、∠A＝∠D D、∠OBC＝∠OCB4. 如图， 是 的外角， ．若 ， ，则 的度数为（ ）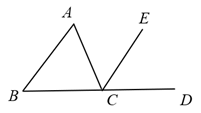
A、 B、 C、 D、5. 如图所示，是一块三角形的草坪，现要在草坪上建一凉亭供大家休息，要使凉亭到草坪三条边的距离相等，凉亭的位置应选在（ ）
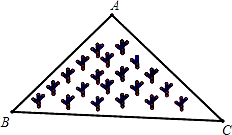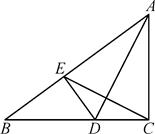
A、△ABC的三条中线的交点 B、△ABC三边的中垂线的交点 C、△ABC三条角平分线的交点 D、△ABC三条高所在直线的交点6. 如图，在△ABC中，∠C＝90°，D，E是AC上两点，且AE＝DE，BD平分∠EBC，那么下列说法中不正确的是（ ）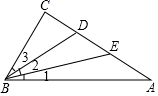
A、BE是△ABD的中线 B、BD是△BCE的角平分线 C、∠1＝∠2＝∠3 D、BC是△ABE的高7. 如图，在 中， ，以点 为圆心，适当长为半径画弧，分别交 于点 ，再分别以点 为圆心，大于 为半径画弧，两弧交于点 ，作射线 交边 于点 ，则 的面积是（ ）
A、 B、 C、 D、8. 具备下列条件的△ABC，不是直角三角形的是（ ）A、∠A+∠B＝∠C B、∠A＝ ∠B＝ ∠C C、∠A＝2∠B＝3∠C D、∠A：∠B：∠C＝1：3：4二、填空题
-
9. 点P（﹣2，3）关于x轴的对称点的坐标是 ．10. 如图，为了使木门不变形，木工师傅在木门上加钉了一根木条，这样是利用三角形的.
11. 若一个多边形的内角和等于720度，则这个多边形的边数是12. 如图所示，AB=DB，∠ABD=∠CBE，请你添加一个适当的条件 ， 使ΔABC≌ΔDBE.(只需添加一个即可)
13. 如图，Rt△ABC中，∠ACB＝90°，∠A＝50°，将其折叠，使点A落在边CB上A′处，折痕为CD ， 则∠A′DB的度数为 ．
14. 如图，在 中， ，分别以点 为圆心，大于 的长为半径画弧，两弧相交于点 作直线 ，交 边于点 ，连接 ，则 的周长为.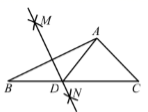
三、解答题
-
15. 把下面的推理过程补充完整，并在括号内注明理由.
已知：如图， ，试说明 .
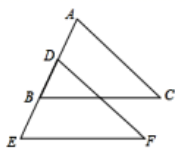
解： （已知）
▲ （_▲_）
在 与 中
（_▲_）
（_▲_）
16. 一个多边形的内角和比外角和的3倍少180°.求：(1)、这个多边形的边数；(2)、该多边形共有多少条对角线.17. 如图，已知点B、E、C、F在一条直线上，且AB＝DF，BE＝CF，∠B＝∠F.求证：AC//DE.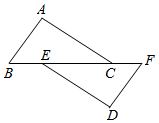
18.(1)、已知：如图1，在△ABC中，请你按下列要求画图（“作图”不要求写作法，但要保留作图痕迹）.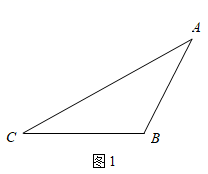
①作∠CBA的角平分线BE，交AC于点E；
②作BC边上的高AD，垂足为点D.
(2)、如图2，在边长为1的小正方形组成的网格中，△ABC的三个顶点分别在网格的格点上，请在网格中作△ABC关于直线l对称的△A1B1C1 ， 并标注相应的字母.
19. 如图，在△ABC中，已知AD是△ABC的角平分线，DE是△ADC的高，∠B＝60°，∠C＝40°，求∠ADB和∠ADE的度数.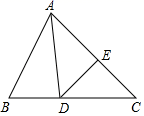
20. 如图所示，B处在A处的南偏西45°方向上，C处在A处的南偏东30°方向，C处在B处的北偏东60°，求∠ACB是多少度？
21. 如图，已知：AB⊥BD，ED⊥BD，AB＝CD，AC＝CE.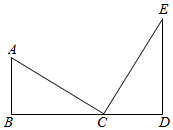
(1)、AC与CE有什么位置关系？(2)、请证明你的结论.
