四川省成都市锦江区2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. 下列立体图形中,主视图是三角形的是( )。A、
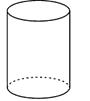 B、
B、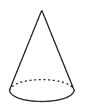 C、
C、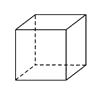 D、
D、 2. 如图,在 中, ,则AC的长为( )
2. 如图,在 中, ,则AC的长为( ) A、5 B、8 C、12 D、133. 用配方法解一元二次方程 ,配方后的方程是( )A、 B、 C、 D、4. 如图,双曲线y= 的一个分支为( )
A、5 B、8 C、12 D、133. 用配方法解一元二次方程 ,配方后的方程是( )A、 B、 C、 D、4. 如图,双曲线y= 的一个分支为( )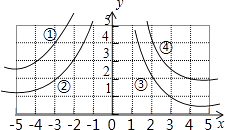 A、① B、② C、③ D、④5. 在一个不透明的布袋中装有9个白球和若干个黑球,它们除颜色不同外,其余均相同。若从中随机摸出一个球,摸到白球的概率是 ,则黑球的个数为( )A、3 B、12 C、18 D、276. 如图,MN所在的直线垂直平分线段AB,利用这样的工具,可以找到圆形工件的圆心,如果使用此工具找到圆心,最少使用次数为( ).
A、① B、② C、③ D、④5. 在一个不透明的布袋中装有9个白球和若干个黑球,它们除颜色不同外,其余均相同。若从中随机摸出一个球,摸到白球的概率是 ,则黑球的个数为( )A、3 B、12 C、18 D、276. 如图,MN所在的直线垂直平分线段AB,利用这样的工具,可以找到圆形工件的圆心,如果使用此工具找到圆心,最少使用次数为( ). A、1 B、2 C、3 D、47. 如图,在 中, ,D为AC上一点,连接BD,且 ,则DC长为( )
A、1 B、2 C、3 D、47. 如图,在 中, ,D为AC上一点,连接BD,且 ,则DC长为( ) A、2 B、 C、 D、58. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 如图,在菱形ABCD中,点E,F分别在AB,CD上,且 ,连接EF交BD于点O连接AO.若 ,则 的度数为( )
A、2 B、 C、 D、58. 若点 在反比例函数 的图象上,则 的大小关系是( )A、 B、 C、 D、9. 如图,在菱形ABCD中,点E,F分别在AB,CD上,且 ,连接EF交BD于点O连接AO.若 ,则 的度数为( )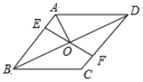 A、50° B、55° C、65° D、75°10. 已知y关于x的函数表达式是 ,下列结论错误的是( )A、若 ,函数的最大值是5 B、若 ,当 时,y随x的增大而增大 C、无论a为何值时,函数图象一定经过点 D、无论a为何值时,函数图象与x轴都有两个交点
A、50° B、55° C、65° D、75°10. 已知y关于x的函数表达式是 ,下列结论错误的是( )A、若 ,函数的最大值是5 B、若 ,当 时,y随x的增大而增大 C、无论a为何值时,函数图象一定经过点 D、无论a为何值时,函数图象与x轴都有两个交点二、填空题
-
11. 如图,将 放在边长为1的小正方形组成的网格中,若点A,O,B都在格点上,则 .
 12. 已知关于x的方程 有两个实数根,则实数k的取值范围为.13. 如图,在矩形ABCD中, ,对角线AC,BD交于点O,点M,N分别为OB,OC的中点,则 的面积为.
12. 已知关于x的方程 有两个实数根,则实数k的取值范围为.13. 如图,在矩形ABCD中, ,对角线AC,BD交于点O,点M,N分别为OB,OC的中点,则 的面积为. 14. 如图,BA,BC是⊙O的两条弦,以点B为圆心任意长为半径画弧,分别交BA,BC于点M,N:分别以点M,N为圆心,以大于 为半径画弧,两弧交于点P,连接BP并延长交 于点D;连接OD,OC.若 ,则 等于.
14. 如图,BA,BC是⊙O的两条弦,以点B为圆心任意长为半径画弧,分别交BA,BC于点M,N:分别以点M,N为圆心,以大于 为半径画弧,两弧交于点P,连接BP并延长交 于点D;连接OD,OC.若 ,则 等于. 15. 若a,b是一元二次方程 的两根,则 .16. 光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率 ( 代表入射角, 代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得 ,则光线从空射入水中的折射率n等于.
15. 若a,b是一元二次方程 的两根,则 .16. 光线从空气射入水中会发生折射现象,发生折射时,满足的折射定律如图①所示:折射率 ( 代表入射角, 代表折射角).小明为了观察光线的折射现象,设计了图②所示的实验;通过细管可以看见水底的物块,但从细管穿过的直铁丝,却碰不上物块,图③是实验的示意图,点A,C,B在同一直线上,测得 ,则光线从空射入水中的折射率n等于.

 17. 如图,在平面直角坐标系中,正方形ABCD的面积为20,顶点A在y轴上,顶点C在x轴上,顶点D在双曲线 的图象上,边CD交y轴于点E,若 ,则k的值为.
17. 如图,在平面直角坐标系中,正方形ABCD的面积为20,顶点A在y轴上,顶点C在x轴上,顶点D在双曲线 的图象上,边CD交y轴于点E,若 ,则k的值为.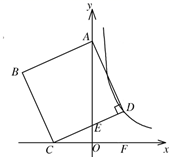 18. 如图,已知 中, ,D是线段AC上一点(不与A,C重合),连接BD,将 沿AB翻折,使点D落在点E处,延长BD与EA的延长线交于点F,若 是直角三角形,则AF的长为.
18. 如图,已知 中, ,D是线段AC上一点(不与A,C重合),连接BD,将 沿AB翻折,使点D落在点E处,延长BD与EA的延长线交于点F,若 是直角三角形,则AF的长为. 19. 如图,在 中, ,对角线 ,点E是线段BC上的动点,连接DE,过点D作DP⊥DE,在射线DP上取点F,使得 ,连接CF,则 周长的最小值为.
19. 如图,在 中, ,对角线 ,点E是线段BC上的动点,连接DE,过点D作DP⊥DE,在射线DP上取点F,使得 ,连接CF,则 周长的最小值为.
三、解答题
-
20.(1)、计算(2)、解方程 .21. 为全面贯彻党的教育方针,坚持“健康第一的教育理念,促进学生健康成长,提高体质健康水平,成都市调整体育中考实施方案:分值增加至60,男1000(女80米)必考,足球、篮球、排球“三选一”……从2019年秋季新入学的七年级起开始实施,某1学为了解七年级学生对三大球类运动的喜爱情况,从七年级学生中随机抽取部分学生进行调查问卷,通过分析整理绘制了如下两幅统计图。请根据两幅统计图中的信息回答下列问题:
 (1)、求参与调查的学生中,喜爱排球运动的学生人数,并补全条形图(2)、若该中学七年级共有400名学生,请你估计该中学七年级学生中喜爱篮球运动的学生有多少名?(3)、若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生,确定为该校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.22. 近日,国产航母山东舰成为了新晋网红,作为我国本世纪建造的第一艘真正意义上的国产航母,承载了我们太多期盼,促使我国在伟大复兴路上加速前行如图,山东舰在一次测试中,巡航到海岛A北偏东60°方向P处,发现在海岛A正东方向有一可疑船只B正沿BA方向行驶。山东舰经测量得出:可疑船只在P处南偏东45°方向,距P处 海里。山东舰立即从P沿南偏西30°方向驶出,刚好在C处成功拦截可疑船只。求被拦截时,可疑船只距海岛A还有多少海里?( ,结果精确到0.1海里)
(1)、求参与调查的学生中,喜爱排球运动的学生人数,并补全条形图(2)、若该中学七年级共有400名学生,请你估计该中学七年级学生中喜爱篮球运动的学生有多少名?(3)、若从喜爱足球运动的2名男生和2名女生中随机抽取2名学生,确定为该校足球运动员的重点培养对象,请用列表法或画树状图的方法求抽取的两名学生为一名男生和一名女生的概率.22. 近日,国产航母山东舰成为了新晋网红,作为我国本世纪建造的第一艘真正意义上的国产航母,承载了我们太多期盼,促使我国在伟大复兴路上加速前行如图,山东舰在一次测试中,巡航到海岛A北偏东60°方向P处,发现在海岛A正东方向有一可疑船只B正沿BA方向行驶。山东舰经测量得出:可疑船只在P处南偏东45°方向,距P处 海里。山东舰立即从P沿南偏西30°方向驶出,刚好在C处成功拦截可疑船只。求被拦截时,可疑船只距海岛A还有多少海里?( ,结果精确到0.1海里) 23. 如图,在 中,E,F分别是 , 上的点,且 ,连接 , , .
23. 如图,在 中,E,F分别是 , 上的点,且 ,连接 , , .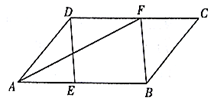 (1)、求证:四边形 是平行四边形.(2)、若 平分 , , , ,求 的长.24. 如图,在直角坐标系中,点B的坐标为 ,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数 的图象交AB,BC分别于点E,F.
(1)、求证:四边形 是平行四边形.(2)、若 平分 , , , ,求 的长.24. 如图,在直角坐标系中,点B的坐标为 ,过点B分别作x轴、y轴垂线,垂足分别是C,A,反比例函数 的图象交AB,BC分别于点E,F. (1)、求直线EF的解析式.(2)、求四边形BEOF的面积.(3)、若点P在y轴上,且 是等腰三角形,请直接写出点P的坐标.25. 如图1, 内接于 ,AD是直径, 的平分线交BD于H,交 于点C,连接DC并延长,交AB的延长线于点E.
(1)、求直线EF的解析式.(2)、求四边形BEOF的面积.(3)、若点P在y轴上,且 是等腰三角形,请直接写出点P的坐标.25. 如图1, 内接于 ,AD是直径, 的平分线交BD于H,交 于点C,连接DC并延长,交AB的延长线于点E. (1)、求证: ;(2)、若 ,求 的值(3)、如图2,连接CB并延长,交DA的延长线于点F,若 ,求 的面积.26. 非洲猪瘟疫情发生以来,猪肉市场供应阶段性偏紧和猪价大幅波动时有发生,为稳定生猪生产,促进转型升级,增强猪肉供应保障能力,国务院办公厅于2019年9月印发了《关于稳定生猪生产促进转型升级的意见》,某生猪饲养场积极响应国家号召,努力提高生产经营管理水平,稳步扩大养殖规模,增加猪肉供应量。该饲养场2019年每月生猪产量y(吨)与月份x( ,且x为整数)之间的函数关系如图所示.
(1)、求证: ;(2)、若 ,求 的值(3)、如图2,连接CB并延长,交DA的延长线于点F,若 ,求 的面积.26. 非洲猪瘟疫情发生以来,猪肉市场供应阶段性偏紧和猪价大幅波动时有发生,为稳定生猪生产,促进转型升级,增强猪肉供应保障能力,国务院办公厅于2019年9月印发了《关于稳定生猪生产促进转型升级的意见》,某生猪饲养场积极响应国家号召,努力提高生产经营管理水平,稳步扩大养殖规模,增加猪肉供应量。该饲养场2019年每月生猪产量y(吨)与月份x( ,且x为整数)之间的函数关系如图所示. (1)、请直接写出当 (x为整数)和 (x为整数)时,y与x的函数关系式;(2)、若该饲养场生猪利润P(万元/吨)与月份x( ,且x为整数)满足关系式: ,请问:该饲养场哪个月的利润最大?最大利润是多少?27. 如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E, .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
(1)、请直接写出当 (x为整数)和 (x为整数)时,y与x的函数关系式;(2)、若该饲养场生猪利润P(万元/吨)与月份x( ,且x为整数)满足关系式: ,请问:该饲养场哪个月的利润最大?最大利润是多少?27. 如图1,在矩形ABCD中,点P是BC边上一点,连接AP交对角线BD于点E, .作线段AP的中垂线MN分别交线段DC,DB,AP,AB于点M,G,F,N.
 (1)、求证: ;(2)、若 ,求 .(3)、如图2,在(2)的条件下,连接CF,求 的值.28. 如图,在平面直角坐标系中,抛物线 的图象与x轴交于 ,B两点,与y轴交于点 ,对称轴 与x轴交于点H.
(1)、求证: ;(2)、若 ,求 .(3)、如图2,在(2)的条件下,连接CF,求 的值.28. 如图,在平面直角坐标系中,抛物线 的图象与x轴交于 ,B两点,与y轴交于点 ,对称轴 与x轴交于点H.
 (1)、求抛物线的函数表达式(2)、直线 与y轴交于点E,与抛物线交于点P,Q(点P在y轴左侧,点Q 在y轴右侧),连接CP,CQ,若 的面积为 ,求点P,Q的坐标.(3)、在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G逆时针旋转90°,使点K恰好落在抛物线上,若存在,请直接写出点K的坐标不存在,请说明理由.
(1)、求抛物线的函数表达式(2)、直线 与y轴交于点E,与抛物线交于点P,Q(点P在y轴左侧,点Q 在y轴右侧),连接CP,CQ,若 的面积为 ,求点P,Q的坐标.(3)、在(2)的条件下,连接AC交PQ于G,在对称轴上是否存在一点K,连接GK,将线段GK绕点G逆时针旋转90°,使点K恰好落在抛物线上,若存在,请直接写出点K的坐标不存在,请说明理由.