四川省阿坝州汶川县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下列方程是一元二次方程的是（）

A、 $x - 1 = 0$ B、 $2 x^{2} - y - 3 = 0$ C、 $x - y + 2 = 0$ D、 $3 x^{2} - 2 x - 1 = 0$

查看试题解析
2. 在下列四个汽车标志图案中，是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 一元二次方程 $- x^{2} + 6 x - 10 = 0$ 的根的情况是（）

A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根

查看试题解析
4. 下列事件是不可能发生的是（）

A、随意掷一枚均匀的硬币两次，至少有一次反面朝上 B、随意掷两个均匀的骰子，朝上面的点数之和为1 C、今年冬天黑龙江会下雪 D、一个转盘被分成6个扇形，按红、白、白、红、红、白排列，转动转盘，指针停在红色区域

查看试题解析
5. 下列函数中，一定是二次函数的是（）

A、 $y = - x^{2} + 1$ B、 $y = a x^{2} + b x + c$ C、 $y = 2 x + 3$ D、 $y = \frac{2}{x^{2}}$

查看试题解析
6. 抛物线 $y = - \frac{1}{5} {(x + 5)}^{2} + 1$ ，下列说法正确的是（）

A、开口向下，顶点坐标 $(5, 1)$ B、开口向上，顶点坐标 $(5, 1)$ C、开口向下，顶点坐标 $(- 5, 1)$ D、开口向上，顶点坐标 $(- 5, 1)$

查看试题解析
7. 已知⊙O的半径为3cm，线段OA=5cm，则点A与⊙O的位置关系是（）

A、A点在⊙O外 B、A点在⊙O上 C、A点在⊙O内 D、不能确定

查看试题解析
8. 今年来某县加大了对教育经费的投入，2013年投入2500万元，2015年投入3500万元．假设该县投入教育经费的年平均增长率为x，根据题意列方程，则下列方程正确的是（　　）

A、2500x²=3500 B、2500（1+x）²=3500 C、2500（1+x%）²=3500 D、2500（1+x）+2500（1+x）²=3500

查看试题解析
9. 抛物线y＝﹣2x²经过平移得到y＝﹣2（x+1）²﹣3，平移方法是（　　）

A、向左平移1个单位，再向下平移3个单位 B、向左平移1个单位，再向上平移3个单位 C、向右平移1个单位，再向下平移3个单位 D、向右平移1个单位，再向上平移3个单位

查看试题解析
10. 如图为二次函数 $y = a x^{2} + b x + c$ 的图象，在下列说法中：

① $a c < 0$ ；②方程 $a x^{2} + b x + c = 0$ 的根是 $x_{1} = - 1 ， x_{2} = 3$ ③ $a + b + c > 0$ ；④当 $x > 1$ 时，y随x的增大而增大；⑤ $2 a - b = 0$ ；⑥ $b^{2} - 4 a c > 0$ ，正确的说法有（）

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析

二、填空题

11. 在直角坐标系中，点（﹣1，2）关于原点对称点的坐标是．

查看试题解析
12. 半径为6 cm的圆内接正四边形的边长是cm．.

查看试题解析
13. 如图， $A B$ 为 $⊙ O$ 的直径， $∠ C D B = 30 ° ，$ 则 $∠ C B A =$ ．

查看试题解析
14. 圣诞节，小红用一张半径为24cm，圆心角为120°的扇形红色纸片做成一个圆锥形的帽子，则这个圆锥形帽子的高为cm．

查看试题解析
15. 设a，b是方程x²+x﹣2018＝0的两个实数根，则（a﹣1）（b﹣1）的值为．

查看试题解析
16. 抛物线y=﹣x²+bx+c的部分图象如图所示，若y＞0，则x的取值范围是．

查看试题解析
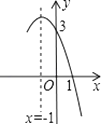17. 关于x的一元二次方程kx²﹣ $\sqrt{4 k + 1}$ x+2=0有两个不相等的实数根，那么k的取值范围是．

查看试题解析
18. 如图，⊙O的半径 $O D ⊥ A B$ 于点C，连接 $A O$ 并延长交⊙O于点E，连接 $E C$ .若 $A B = 4 ， C D = 1$ ，则 $E C$ 的长为 .

查看试题解析
19. 如图，一段抛物线 $y = - x (x - 1) (0 \leq x \leq 1)$ 记为 $m_{1}$ ，它与x轴的交点为 $O ， A_{1}$ ，顶点为 $P_{1}$ ；将 $m_{1}$ 绕点 $A_{1}$ 旋转180°得到 $m_{2}$ ，交x轴于点为 $A_{2}$ ，顶点为 $P_{2}$ ；将 $m_{2}$ 绕点 $A_{2}$ 旋转180°得到 $m_{3}$ ，交x轴于点为 $A_{3}$ ，顶点为 $P_{3}$ ；……，如此进行下去，直至到 $m_{10}$ ，顶点为 $P_{10}$ ，则顶点 $P_{10}$ 的坐标为．

查看试题解析

三、解答题

20. 用配方法解一元二次方程
$x^{2} - 6 x - 7 = 0$

查看试题解析
21. 已知关于x的方程 $2 x^{2} + k x - 1 = 0$

(1)、求证：方程有两个不相等的实数根．

(2)、若方程的一个根是 $x = - 1,$ 求另一个根及k的值．

查看试题解析
22. 如图，点A的坐标为 $(3 ， 3)$ ，点B的坐标为 $(4 ， 0)$ .点C的坐标为 $(0 ， - 1)$ .

⑴请在直角坐标系中画出 $△ A B C$ 绕着点C逆时针旋转 $90 °$ 后的图形 $△ A' B' C$ .

⑵直接写出：点 $A'$ 的坐标（），

⑶点 $B^{'}$ 的坐标（）.

查看试题解析
23. 如图，点E是△ABC的内心，AE的延长线与△ABC的外接圆相交于点D．

(1)、若∠BAC=70°，求∠CBD的度数；

(2)、求证：DE=DB．

查看试题解析
24. 自贡是“盐之都，龙之乡，灯之城”，文化底蕴深厚.为弘扬乡土特色文化，某校就同学们对“自贡历史文化”的了解程度进行随机抽样调查，将调查结果绘制成如下两幅统计图：

(1)、本次共调查名学生，条形统计图中m= ；

(2)、若该校共有学生1200名，则该校约有名学生不了解“自贡历史文化”；

(3)、调查结果中，该校九年级（2）班学生中了解程度为“很了解”的同学进行测试，发现其中共有四名同学相当优秀，它们是三名男生，一名女生，现准备从这四名同学中随机抽取两人去市里参加“自贡历史文化”知识竞赛，用树状图或列表法，求恰好抽取一男生一女生的概率.

查看试题解析
25. 如图，在 $R t △ A B C$ 中， $∠ B = 90 °$ ， $∠ A$ 的平分线交 $B C$ 于 $D$ ， $E$ 为 $A B$ 上一点， $D E = D C$ ，以 $D$ 为圆心，以 $D B$ 的长为半径画圆.

(1)、求证： $A C$ 是⊙ $D$ 的切线；

(2)、求证： $A B + E B = A C$ .

查看试题解析
26. 如图，要利用一面足够长的墙为一边，其余三边用总长 33m 的围栏建两个面积相同的生态园，为了出入方便，每个生态园在平行于墙的一边各留了一个宽 1.5 米的门，能够建生态园的场地垂直于墙的一边长不超过 6 米（围栏宽忽略不计)．

(1)、每个生态园的面积为 48 平方米，求每个生态园的边长；

(2)、每个生态园的面积(填“能”或“不能”）达到 108 平方米．(直接填答案）

查看试题解析
27. 某水果批发商销售每箱进价为40元的苹果，物价部门规定每箱售价不得高于55元，市场调查发现，若每箱以50元的价格销售，平均每天销售90箱，价格每提高1元，平均每天少销售3箱.

(1)、求平均每天销售量 $y$ 箱与销售价 $x$ 元/箱之间的函数关系式.

(2)、求该批发商平均每天的销售利润w（元）与销售价 $x$ （元/箱）之间的函数关系式.

(3)、当每箱苹果的销售价为多少元时，可以获得最大利润？最大利润是多少？

查看试题解析
28. 如图，抛物线 $y = a x^{2} + 2 x + c$ 经过点 $A (0 ， 3) ， B (- 1 ， 0)$ ，请解答下列问题：

(1)、求抛物线的解析式；

(2)、抛物线的顶点为点D，对称轴与x轴交于点E，连接 $B D$ ，求 $B D$ 的长．

(3)、点F在抛物线的对称轴上运动，是否存在点F，使 $△ B F C$ 的面积为 $4$ ，如果存在，直接写出点F的坐标；如果不存在，请说明理由．

查看试题解析