湖南省株洲市芦淞区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 计算 ${(- 3)}^{2}$ 的结果等于（）

A、-6 B、6 C、-9 D、9

查看试题解析
2. 若 $a : b = 3 : 4$ ，且 $a = 6$ ，则 $2 a - b$ 的值是（）

A、4 B、2 C、20 D、14

查看试题解析
3. 已知反比例函数的解析式为 $y = \frac{| a | - 2}{x}$ ，则a的取值范围是 $($ 　　 $)$

A、 $a \neq 2$ B、 $a \neq - 2$ C、 $a \neq \pm 2$ D、 $a = \pm 2$

查看试题解析
4. 如果 $\sin 30 ° = \cos A$ ，那么锐角A的度数是（）

A、60° B、45° C、30° D、20°

查看试题解析
5. 抛物线 $y = {(x - 1)}^{2} + 2$ 的对称轴是（）

A、直线x＝－1 B、直线x＝1 C、直线x＝－2 D、直线x＝2

查看试题解析
6. 质检部门对某酒店的餐纸进行调查，随机调查5包(每包5片)，5包中合格餐纸(单位：片)分别为4，5，4，5，5，则估计该酒店的餐纸的合格率为（）

A、95% B、97% C、92% D、98%

查看试题解析
7. 若关于x的一元二次方程 $x^{2} - 2 x + m = 0$ 有实数根，则实数m的取值范围是（）

A、 $m < 1$ B、 $m \leq 1$ C、 $m > 1$ D、 $m \geq 1$

查看试题解析
8. 如图，某地修建高速公路，要从A地向B地修一条隧道（点A、B在同一水平面上）．为了测量A、B两地之间的距离，一架直升飞机从A地出发，垂直上升800米到达C处，在C处观察B地的俯角为α，则A、B两地之间的距离为（　　）

A、800sinα米 B、800tanα米 C、 $\frac{800}{\sin α}$ 米 D、 $\frac{800}{\tan α}$ 米

查看试题解析
9. 在如图所示的象棋盘（各个小正方形的边长均相等）中，根据“马走日”的规则，“马”应落在下列哪个位置处，能使“马”、“车”、“炮”所在位置的格点构成的三角形与“帅”、“相”，“兵”所在位置的格点构成的三角形相似（）

A、①处 B、②处 C、③处 D、④处

查看试题解析
10. 函数 $y = x^{2} + b x + c$ 与 $y = x$ 的图象如图所示，有以下结论：①b²－4c＞0；②b＋c＝0；③3b＋c＋6＝0；④当1＜x＜3时， $x^{2} + (b - 1) x + c$ ＜0．其中正确的个数为（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

11. 函数 $y = \sqrt{x - 2}$ 中自变量x的取值范围是．

查看试题解析
12. 质检部门为了检测某品牌电器的质量，从同一批次共10000件产品中随机柚取100件进行检测，检测出次品5件，由此估计这一批产品中的次品件数是．

查看试题解析
13. 如图，旗杆高AB＝8m ，某一时刻，旗杆影子长BC＝16m ，则tanC＝．

查看试题解析
14. 若 $x_{1} 、 x_{2}$ 是一元二次方程 $x^{2} - 3 x + 1 = 0$ 的两个根，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ ＝．

查看试题解析
15. 学校门口的栏杆如图所示，栏杆从水平位置BD绕O点旋转到AC位置，已知AB⊥BD，CD⊥BD，垂足分别为B，D，AO=4m，AB=1.6m，CO=1m，则栏杆C端应下降的垂直距离CD为.

查看试题解析
16. 如图，B（3，﹣3），C（5，0），以OC，CB为边作平行四边形OABC，则经过点A的反比例函数的解析式为.

查看试题解析
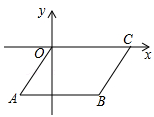17. 把抛物线 $y = x^{2} + b x + c$ 的图像向右平移 $3$ 个单位，再向下平移 $2$ 个单位，所得图像的解析式为 $y = x^{2} - 2 x + 3$ ,则b的值为．

查看试题解析
18. 《道德经》中的“道生一，一生二，二生三，三生万物”道出了自然数的特征．在数的学习过程中，我们会对其中一些具有某种特性的数进行研究，如学习自然数时，我们研究了奇数、偶数、质数、合数等．现在我们来研究另一种特珠的自然数——“纯数”．定义：对于自然数n，在计算n+(n+1)+(n+2)时，各数位都不产生进位，则称这个自然数n为“纯数”，例如：32是“纯数”，因为计算32+33+34时，各数位都不产生进位；23不是“纯数”，因为计算23+24＋25时，个位产生了进位．那么，小于100的自然数中，“纯数”的个数为个．

查看试题解析

三、解答题

19. 计算： $2 \tan 60 ° + {(- 1)}^{2019} - \sqrt{12}$

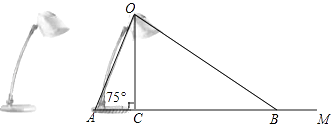
查看试题解析
20. 先化简，后求值： $(\frac{1}{x + 1} + \frac{1}{x - 1}) \div \frac{x^{2} - x}{x^{2} - 2 x + 1}$ ，其中 $x = \sqrt{2} - 1$ ．

查看试题解析
21. 如图为放置在水平桌面上的台灯的平面示意图，灯臂AO长为40cm，与水平面所形成的夹角∠OAM为75°．由光源O射出的边缘光线OC，OB与水平面所形成的夹角∠OCA，∠OBA分别为90°和30°，求该台灯照亮水平面的宽度BC（不考虑其他因素，结果精确到0.1cm．温馨提示：sin75°≈0.97，cos75°≈0.26， $\sqrt{3} \approx 1.73$ ）．

查看试题解析

22. 前苏联教育家苏霍姆林斯曾说过：“让学生变聪明的方法，不是补课，不是増加作业量，而是阅读，阅读，再阅读”.课外阅读也可以促进我们养成终身学习的习惯.云南某学校组织学生利用课余时间多读书，读好书，一段时间后，学校对部分学生每周阅读时间进行调查，并绘制了不完整的频数分布表和频数分布直方图，如图所示：

时间（时）	频数	百分比
$0 \leq x < 3$	10	10%
$3 \leq x < 6$	25	m
$6 \leq x < 9$	n	30%
$9 \leq x < 12$	a	20%
$12 \leq x < 15$	15	15%

根据图表提供的信息，回答下列问题：

(1)、填空：m= ， n=；

(2)、请补全频数分布直方图；

(3)、该校共有3600名学生，估计学生每周阅读时间x（时）在

6 \leq x < 12

范围内的人数有多少人？

查看试题解析

23. 如图所示的是夹文件用的铁(塑料)夹子在常态下的侧面示意图．AC，BC表示铁夹的两个面，O点是轴，OD⊥AC于点D，且AD＝15mm，DC＝24mm，OD＝10mm．已知文件夹是轴对称图形，试利用图②，求图①中A，B两点间的距离．

查看试题解析
24. 如图，在△ABC中，D是BC边上的中点，且AD＝AC，DE⊥BC，DE与AB相交于点E，EC与AD相交于点F．

(1)、求证：△ABC∽△FCD；

(2)、若S_△_ABC＝20，BC＝10，求DE的长．

查看试题解析
25. 如图，在平面直角坐标系中，直线AB与y轴交于点 $B (0 ， 7)$ ，与反比例函数 $y = \frac{- 8}{x}$ 在第二象限内的图象相交于点 $A (- 1 ， a)$ ．

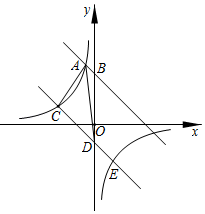(1)、求直线AB的解析式；

(2)、将直线AB向下平移9个单位后与反比例函数的图象交于点C和点E ，与y轴交于点D ，求 $Δ A C D$ 的面积；

(3)、设直线CD的解析式为 $y = m x + n$ ，根据图象直接写出不等式 $m x + n \leq \frac{- 8}{x}$ 的解集．

查看试题解析
26. 如图，已知抛物线 $y = a x^{2} + b x + c (a \neq 0)$ 与x轴交于A（﹣1，0）、B（3，0）两点，与y轴交于点C，直线 $y = - 2 x + 3$ 经过点C，与x轴交于点D．

(1)、求该抛物线的函数关系式；

(2)、点P是（1）中的抛物线上的一个动点，设点P的横坐标为t（0＜t＜3）．
①求△PCD的面积的最大值；

②是否存在点P，使得△PCD是以CD为直角边的直角三角形？若存在，求点P的坐标；若不存在，请说明理由．

查看试题解析