湖南省长沙市雅礼教育集团2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. 下列实数: ,其中最大的实数是( )A、-2020 B、 C、 D、2. 据路透社报道,中国华为技术有限公司推出新的服务器芯片组,此举正值中国努力提高芯片制造能力,并减少对进口芯片的严重依赖.华为技术部门还表示,电子元件的尺寸大幅度缩小,在芯片上某种电子元件大约只占有面积 .其中0.00000065用科学记数法表示为( )A、 B、 C、 D、3. 下列运算正确的是( )A、 B、 C、 D、4. 下列说法正确的是( )A、对角线相等的四边形一定是矩形 B、任意掷一枚质地均匀的硬币10次,一定有5次正面向上 C、如果有一组数据为5,3,6,4,2,那么它的中位数是6 D、“用长分别为 、12cm、 的三条线段可以围成三角形”这一事件是不可能事件5. 某个几何体的三视图如图所示,该几何体是( )
 A、
A、 B、
B、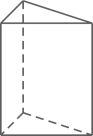 C、
C、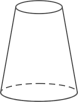 D、
D、 6. 若△ABC∽△ADE,若AB=9,AC=6,AD=3,则EC的长是( )
6. 若△ABC∽△ADE,若AB=9,AC=6,AD=3,则EC的长是( )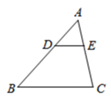 A、2 B、3 C、4 D、57. 如图,在⊙O中,点A、B、C在圆上,∠AOB=100°,则∠C=( )
A、2 B、3 C、4 D、57. 如图,在⊙O中,点A、B、C在圆上,∠AOB=100°,则∠C=( )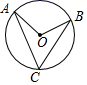 A、45° B、50° C、55° D、60°8. 如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN , 交BC于点D , 连接AD , 则∠CAD的度数是( )
A、45° B、50° C、55° D、60°8. 如图,Rt△ABC中,∠C=90°,∠B=30°,分别以点A和点B为圆心,大于 的长为半径作弧,两弧相交于M、N两点,作直线MN , 交BC于点D , 连接AD , 则∠CAD的度数是( )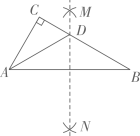 A、20° B、30° C、45° D、60°9. 如图,已知 和 是以点O为位似中心的位似图形,且 和 的周长之比为 ,点B的坐标为 ,则点 的坐标为( ).
A、20° B、30° C、45° D、60°9. 如图,已知 和 是以点O为位似中心的位似图形,且 和 的周长之比为 ,点B的坐标为 ,则点 的坐标为( ). A、 B、 C、 D、10. 如图,△ABC中,AB=25,BC=7,CA=24.则sinA的值为( )
A、 B、 C、 D、10. 如图,△ABC中,AB=25,BC=7,CA=24.则sinA的值为( )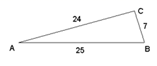 A、 B、 C、 D、11. 程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.对书中某一问题改编如下:意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个正好分完,大和尚共分得( )个馒头
A、 B、 C、 D、11. 程大位是我国明朝商人,珠算发明家.他60岁时完成的《直指算法统宗》是东方古代数学名著,详述了传统的珠算规则,确立了算盘用法.对书中某一问题改编如下:意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个正好分完,大和尚共分得( )个馒头 A、25 B、72 C、75 D、9012. 设抛物线 的顶点为M ,与y轴交于N点,连接直线MN,直线MN与坐标轴所围三角形的面积记为S.下面哪个选项的抛物线满足S=1 ( )A、 B、 C、 D、 (a为任意常数)
A、25 B、72 C、75 D、9012. 设抛物线 的顶点为M ,与y轴交于N点,连接直线MN,直线MN与坐标轴所围三角形的面积记为S.下面哪个选项的抛物线满足S=1 ( )A、 B、 C、 D、 (a为任意常数)二、填空题
-
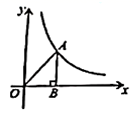
13. 分解因式 .14. 如图,点A在反比例函数 的图象上, 轴,垂足为B,且 ,则 .
 15. 不等式组 的解集是 .16. 某圆锥的底面半径是2,母线长是6,则该圆锥的侧面积等于 .17. 如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH.若OB=4,S菱形ABCD=24,则OH的长为.
15. 不等式组 的解集是 .16. 某圆锥的底面半径是2,母线长是6,则该圆锥的侧面积等于 .17. 如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH.若OB=4,S菱形ABCD=24,则OH的长为.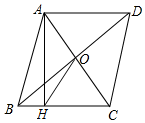 18. 如图,已知点A的坐标为(4,0),点B的坐标为(0,3),在第一象限内找一点P(a,b) ,使△PAB为等边三角形,则2(a-b)= .
18. 如图,已知点A的坐标为(4,0),点B的坐标为(0,3),在第一象限内找一点P(a,b) ,使△PAB为等边三角形,则2(a-b)= .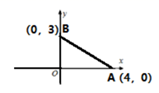
三、解答题
-
19. 计算:20. 先化简,再求值: ,其中a=2.21. 为深化课程改革,提高学生的综合素质,我校开设了形式多样的校本课程.为了解校本课程在学生中最受欢迎的程度,学校随机抽取了部分学生进行调查,从A:天文地理;B:科学探究;C:文史天地;D:趣味数学;四门课程中选你喜欢的课程(被调查者限选一项),并将调查结果绘制成两个不完整的统计图,如图所示,根据以上信息,解答下列问题:
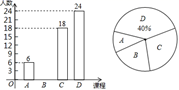 (1)、本次调查的总人数为人,扇形统计图中A部分的圆心角是度;(2)、请补全条形统计图;(3)、根据本次调查,该校400名学生中,估计最喜欢“科学探究”的学生人数为多少?(4)、为激发学生的学习热情,学校决定举办学生综合素质大赛,采取“双人同行,合作共进”小组赛形式,比赛题目从上面四个类型的校本课程中产生,并且规定:同一小组的两名同学的题目类型不能相同,且每人只能抽取一次,小琳和小金组成了一组,求他们抽到“天文地理”和“趣味数学”类题目的概率是多少?(请用画树状图或列表的方法求)22. 天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知 米, 米,AB与水平线 的夹角是 ,BC与水平线 的夹角是 .求:本次检修中,检修人员上升的垂直高度 是多少米?(结果精确到1米,参考数据: )
(1)、本次调查的总人数为人,扇形统计图中A部分的圆心角是度;(2)、请补全条形统计图;(3)、根据本次调查,该校400名学生中,估计最喜欢“科学探究”的学生人数为多少?(4)、为激发学生的学习热情,学校决定举办学生综合素质大赛,采取“双人同行,合作共进”小组赛形式,比赛题目从上面四个类型的校本课程中产生,并且规定:同一小组的两名同学的题目类型不能相同,且每人只能抽取一次,小琳和小金组成了一组,求他们抽到“天文地理”和“趣味数学”类题目的概率是多少?(请用画树状图或列表的方法求)22. 天门山索道是世界最长的高山客运索道,位于张家界天门山景区.在一次检修维护中,检修人员从索道A处开始,沿A﹣B﹣C路线对索道进行检修维护.如图:已知 米, 米,AB与水平线 的夹角是 ,BC与水平线 的夹角是 .求:本次检修中,检修人员上升的垂直高度 是多少米?(结果精确到1米,参考数据: ) 23. 2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.(1)、问:今年年初猪肉的价格为每千克多少元?(2)、某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?24. 如图,在 中,点O在斜边 上,以 为圆心, 为半径作圆,分别与 、 相交于点D、E,连接 ,已知 .
23. 2018年非洲猪瘟疫情暴发后,今年猪肉价格不断走高,引起了民众与政府的高度关注,据统计:今年7月20日猪肉价格比今年年初上涨了60%,某市民今年7月20日在某超市购买1千克猪肉花了80元钱.(1)、问:今年年初猪肉的价格为每千克多少元?(2)、某超市将进货价为每千克65元的猪肉,按7月20日价格出售,平均一天能销售出100千克,经调查表明:猪肉的售价每千克下降1元,其日销售量就增加10千克,超市为了实现销售猪内每天有1560元的利润,并且可能让顾客得到实惠,猪肉的售价应该下降多少元?24. 如图,在 中,点O在斜边 上,以 为圆心, 为半径作圆,分别与 、 相交于点D、E,连接 ,已知 .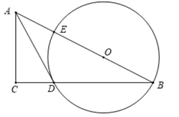 (1)、求证: 是 的切线;(2)、若 , ,求劣弧 与弦 所围阴影图形的面积;(3)、若 , ,求 的长.25. 有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”.
(1)、求证: 是 的切线;(2)、若 , ,求劣弧 与弦 所围阴影图形的面积;(3)、若 , ,求 的长.25. 有一组邻边相等的凸四边形叫做“和睦四边形”,寓意是全世界和平共处,睦邻友好,共同发展.如菱形,正方形等都是“和睦四边形”. (1)、如图1,BD平分∠ABC,AD∥BC,求证:四边形ABCD为“和睦四边形”;(2)、如图2,直线 与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;(3)、如图3,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:① ;②顶点D在以AB为直径的圆上. 点 是抛物线 上任意一点,且 .若 恒成立,求m的最小值.26. 如图1,在平面直角坐标系 中,函数 (m为常数, , )的图象经过点 和 ,直线 与x轴,y轴分别交于C,D两点.
(1)、如图1,BD平分∠ABC,AD∥BC,求证:四边形ABCD为“和睦四边形”;(2)、如图2,直线 与x轴、y轴分别交于A、B两点,点P、Q分别是线段OA、AB上的动点.点P从点A出发,以每秒4个单位长度的速度向点O运动.点Q从点A出发,以每秒5个单位长度的速度向点B运动.P、Q两点同时出发,设运动时间为t秒.当四边形BOPQ为“和睦四边形”时,求t的值;(3)、如图3,抛物线 与x轴交于A、B两点(点A在点B的左侧),与y轴交于点C,抛物线的顶点为点D.当四边形COBD为“和睦四边形”,且CD=OC.抛物线还满足:① ;②顶点D在以AB为直径的圆上. 点 是抛物线 上任意一点,且 .若 恒成立,求m的最小值.26. 如图1,在平面直角坐标系 中,函数 (m为常数, , )的图象经过点 和 ,直线 与x轴,y轴分别交于C,D两点.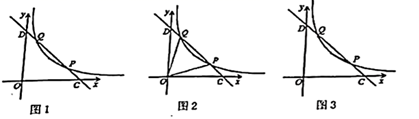 (1)、求 的度数;(2)、如图2,连接 、 ,当 时,求此时m的值:(3)、如图3,点A,点B分别在x轴和y轴正半轴上的动点.再以 、 为邻边作矩形 .若点M恰好在函数 (m为常数, , )的图象上,且四边形 为平行四边形,求此时 、 的长度.
(1)、求 的度数;(2)、如图2,连接 、 ,当 时,求此时m的值:(3)、如图3,点A,点B分别在x轴和y轴正半轴上的动点.再以 、 为邻边作矩形 .若点M恰好在函数 (m为常数, , )的图象上,且四边形 为平行四边形,求此时 、 的长度.