湖南省长沙市天心区长郡教育集团2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. ﹣ 的绝对值为( )A、﹣2 B、﹣ C、 D、12. PM2.5是大气压中直径小于或等于0.0000025m的颗粒物,将0.0000025用科学记数法表示为( )A、0.25×10﹣5 B、0.25×10﹣6 C、2.5×10﹣5 D、2.5×10﹣63. 使分式 有意义的x的取值范是( )A、x≠3 B、x=3 C、x≠0 D、x=04. 在下列各式中,运算结果正确的是( )A、x2+x2=x4 B、x﹣2x=﹣x C、x2•x3=x6 D、(x﹣1)2=x2﹣15. 如图,已知AB∥CD,AD=CD,∠1=40°,则∠2的度数为( )
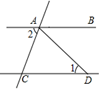 A、60° B、65° C、70° D、75°6. 如图,△ABC是⊙O的内接三角形,∠AOB=110°,则∠ACB的度数为( )
A、60° B、65° C、70° D、75°6. 如图,△ABC是⊙O的内接三角形,∠AOB=110°,则∠ACB的度数为( )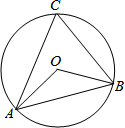 A、35° B、55° C、60° D、70°7. 如图,在△ABC中,AB的垂直平分线交BC于D,AC的中垂线交BC于E,∠DAE=20°,则∠BAC的度数为( )
A、35° B、55° C、60° D、70°7. 如图,在△ABC中,AB的垂直平分线交BC于D,AC的中垂线交BC于E,∠DAE=20°,则∠BAC的度数为( )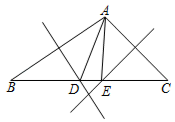 A、70° B、80° C、90° D、100°8. 下面哪个图形不是正方体的平面展开图( )A、
A、70° B、80° C、90° D、100°8. 下面哪个图形不是正方体的平面展开图( )A、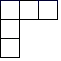 B、
B、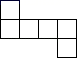 C、
C、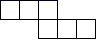 D、
D、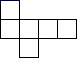 9. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的概率是0.2,则估计盒子中大约有红球( )A、12个 B、16个 C、20个 D、25个10. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”设鸡x只,兔y只,可列方程组为( )
9. 在一个不透明的口袋中,装有若干个红球和4个黄球,它们除颜色外没有任何区别,摇匀后从中随机摸出一个球,记下颜色后再放回口袋中,通过大量重复摸球实验发现,摸到黄球的概率是0.2,则估计盒子中大约有红球( )A、12个 B、16个 C、20个 D、25个10. 我国古代数学著作《孙子算经》中有“鸡兔同笼”问题:“今有鸡兔同笼,上有三十五头,下有九十四足,问鸡兔各几何.”设鸡x只,兔y只,可列方程组为( )
A、 B、 C、 D、11. 如图,平行于x轴的直线与函数y= (k1>0,x>0),y= (k2>0,x>0)的图象分别相交于A,B两点,点A在点B的右侧,C为x轴上的一个动点,若△ABC的面积为6,则k1﹣k2的值为( ) A、12 B、﹣12 C、6 D、﹣612. 已知抛物线y=x2+(2a+1)x+a2﹣a,则抛物线的顶点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限
A、12 B、﹣12 C、6 D、﹣612. 已知抛物线y=x2+(2a+1)x+a2﹣a,则抛物线的顶点不可能在( )A、第一象限 B、第二象限 C、第三象限 D、第四象限二、填空题
-
13. 不等式 >4﹣x的解集为 .14. 已知在平面直角坐标系中,点 在第二象限,且到 轴的距离为3,到 轴的距离为4,则点 的坐标为 .15. 高为8米的旗杆在水平地面上的影子长为6米,同一时刻测得附近一个建筑物的影子长30米,则此建筑物的高度为米.16. 分解因式: .17. 如图,直线y=ax+b过点A(0,2)和点B(﹣3,0),则方程ax+b=0的解是 .
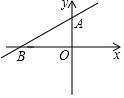 18. 如图,⊙O是锐角△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.下列结论:①AF平分∠BAC;②点F为△BDC的外心;③ ;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是(把你认为正确结论的序号都填上).
18. 如图,⊙O是锐角△ABC的外接圆,FH是⊙O的切线,切点为F,FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.下列结论:①AF平分∠BAC;②点F为△BDC的外心;③ ;④若点M,N分别是AB和AF上的动点,则BN+MN的最小值是ABsin∠BAC.其中一定正确的是(把你认为正确结论的序号都填上).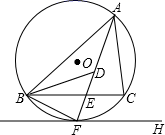
三、解答题
-
19. 计算 .20. 先化简,再求值: ,其中﹣2≤a≤2,从中选一个你喜欢的整数代入求值.21. 为了解某校九年级学生立定跳远水平,随机抽取该年级50名学生进行测试,并把测试成绩(单位:m)绘制成不完整的频数分布表和频数分布直方图.
学生立定跳远测试成绩的频数分布表
分组
频数
1.2≤x<1.6
a
1.6≤x<2.0
12
2.0≤x<2.4
b
2.4≤x<2.8
10
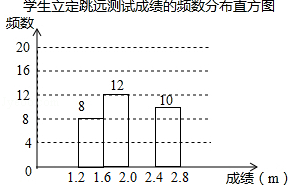
请根据图表中所提供的信息,完成下列问题:
(1)、表中a= , b= , 样本成绩的中位数落在范围内;
(2)、请把频数分布直方图补充完整;(3)、该校九年级共有1000名学生,估计该年级学生立定跳远成绩在2.4≤x<2.8范围内的学生有多少人?22. 如图,在四边形ABCD中,AD∥BC,AC与BD交于点E,点E是BD的中点,延长CD到点F,使DF=CD,连接AF,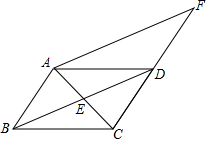 (1)、求证:AE=CE;(2)、求证:四边形ABDF是平行四边形;(3)、若AB=2,AF=4,∠F=30°,则四边形ABCF的面积为 .23. A、B两地间的距离为15千米,甲从A地出发步行前往B地,20分钟后,乙从 B地出发骑车前往A地,且乙骑车比甲步行每小时多走10千米.乙到达A地后停留40分钟,然后骑车按原路原速返回,结果甲、乙两人同时到达B地.求甲从A地到B地步行所用的时间.24. 如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.
(1)、求证:AE=CE;(2)、求证:四边形ABDF是平行四边形;(3)、若AB=2,AF=4,∠F=30°,则四边形ABCF的面积为 .23. A、B两地间的距离为15千米,甲从A地出发步行前往B地,20分钟后,乙从 B地出发骑车前往A地,且乙骑车比甲步行每小时多走10千米.乙到达A地后停留40分钟,然后骑车按原路原速返回,结果甲、乙两人同时到达B地.求甲从A地到B地步行所用的时间.24. 如图,四边形ABCD的外接圆为⊙O,AD是⊙O的直径,过点B作⊙O的切线,交DA的延长线于点E,连接BD,且∠E=∠DBC.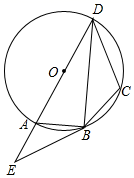 (1)、求证:DB平分∠ADC;(2)、若CD=9,tan∠ABE= ,求⊙O的半径.25. 如图1,抛物线W:y=ax2﹣2的顶点为点A,与x轴的负半轴交于点D,直线AB交抛物线W于另一点C,点B的坐标为(1,0).
(1)、求证:DB平分∠ADC;(2)、若CD=9,tan∠ABE= ,求⊙O的半径.25. 如图1,抛物线W:y=ax2﹣2的顶点为点A,与x轴的负半轴交于点D,直线AB交抛物线W于另一点C,点B的坐标为(1,0).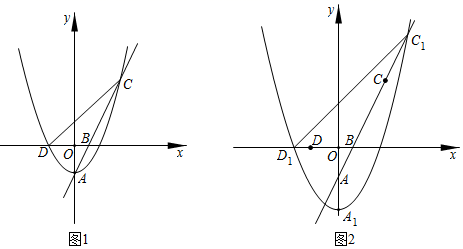 (1)、求直线AB的解析式;(2)、过点C作CE⊥x轴,交x轴于点E,若AC平分∠DCE,求抛物线W的解析式;(3)、若a= ,将抛物线W向下平移m(m>0)个单位得到抛物线W1 , 如图2,记抛物线W1的顶点为A1 , 与x轴负半轴的交点为D1 , 与射线BC的交点为C1 . 问:在平移的过程中,tan∠D1C1B是否恒为定值?若是,请求出tan∠D1C1B的值;若不是,请说明理由.26. 在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.
(1)、求直线AB的解析式;(2)、过点C作CE⊥x轴,交x轴于点E,若AC平分∠DCE,求抛物线W的解析式;(3)、若a= ,将抛物线W向下平移m(m>0)个单位得到抛物线W1 , 如图2,记抛物线W1的顶点为A1 , 与x轴负半轴的交点为D1 , 与射线BC的交点为C1 . 问:在平移的过程中,tan∠D1C1B是否恒为定值?若是,请求出tan∠D1C1B的值;若不是,请说明理由.26. 在平面直角坐标系中,点到直线的距离即为点到直线的垂线段的长.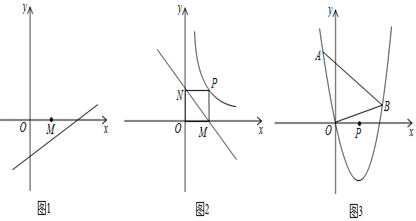 (1)、如图1,取点M(1,0),则点M到直线l:y= x﹣1的距离为多少?(2)、如图2,点P是反比例函数y= 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0 , 问是否存在点P,使d0= ?若存在,求出点P的坐标,若不存在,请说明理由.(3)、如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.
(1)、如图1,取点M(1,0),则点M到直线l:y= x﹣1的距离为多少?(2)、如图2,点P是反比例函数y= 在第一象限上的一个点,过点P分别作PM⊥x轴,作PN⊥y轴,记P到直线MN的距离为d0 , 问是否存在点P,使d0= ?若存在,求出点P的坐标,若不存在,请说明理由.(3)、如图3,若直线y=kx+m与抛物线y=x2﹣4x相交于x轴上方两点A、B(A在B的左边).且∠AOB=90°,求点P(2,0)到直线y=kx+m的距离最大时,直线y=kx+m的解析式.