湖南省岳阳市岳阳县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. 已知 ,下列变形错误的是( )A、 B、 C、 D、2. 下列关于反比例函数 ,结论正确的是( )A、图象必经过 B、图象在二,四象限内 C、在每个象限内,y随x的增大而减小 D、当 时,则3. 甲、乙、丙、丁四人各进行了10次射击测试,他们的平均成绩相同,方差分别是 , , , ,则射击成绩最稳定的是( )A、甲 B、乙 C、丙 D、丁4. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、5. 将抛物线 的图象先向右平移2个单位,再向上平移3个单位后,得到的抛物线的解析式是( )A、 B、 C、 D、6. 已知关于x的一元二次方程 有两个相等的实数根,则锐角 等于( )A、 B、 C、 D、7. 国家实施”精准扶贫“政策以来,很多贫困人口走向了致富的道路.某地区2016年底有贫困人口9万人,通过社会各界的努力,2018年底贫困人口减少至1万人.设2016年底至2018年底该地区贫困人口的年平均下降率为 ,根据题意列方程得( )A、 B、 C、 D、8. 如图,等腰 与等腰 是以点O为位似中心的位似图形,位似比为 ,则点D的坐标是( )
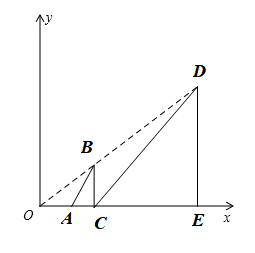 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 方程的解是 .10. 已知 ,相似比为 ,且 的面积为 ,则 的面积为 .11. 如图,某水坝的坡比为 ,坡长 为 米,则该水坝的高度BC为米.
 12. 中, 如果锐角 满足 ,则 度13. 已知m是方程 的一个根,则代数式 的值为 .14. 抛物线 经过点 ,则这条抛物线的对称轴是直线 .15. 如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数 (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 .
12. 中, 如果锐角 满足 ,则 度13. 已知m是方程 的一个根,则代数式 的值为 .14. 抛物线 经过点 ,则这条抛物线的对称轴是直线 .15. 如图,在直角坐标系中,正方形的中心在原点O,且正方形的一组对边与x轴平行,点P(3a,a)是反比例函数 (k>0)的图象上与正方形的一个交点.若图中阴影部分的面积等于9,则这个反比例函数的解析式为 .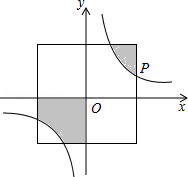 16. 如图, 的对角线 交于点 平分 交 于点E,交 于点F,且 ,连接 .下列结论:① ;② ;③ :④ 其中正确的结论有(填写所有正确结论的序号)
16. 如图, 的对角线 交于点 平分 交 于点E,交 于点F,且 ,连接 .下列结论:① ;② ;③ :④ 其中正确的结论有(填写所有正确结论的序号)
三、解答题
-
17. 计算:18. 已知二次函数的图象顶点是 , 且经过 ,求这个二次函数的表达式.19. 如图,已知 中, , 点D是边 上一点,且
 (1)、求证: ;(2)、求证: .20. 某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.请根据图表信息,解答下列问题:
(1)、求证: ;(2)、求证: .20. 某学校开展了主题为“垃圾分类,绿色生活新时尚”的宣传活动,为了解学生对垃圾分类知识的掌握情况,该校环保社团成员在校园内随机抽取了部分学生进行问卷调查将他们的得分按优秀、良好、合格、不合格四个等级进行统计,并绘制了如下不完整的统计表和条形统计图.请根据图表信息,解答下列问题:等级
频数
频率
优秀
21
0.42
良好
m
0.40
合格
6
n
不合格
3
0.06
 (1)、本次调查随机抽取了 名学生:表中 ;(2)、补全条形统计图:(3)、若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀"和“良好”等级的学生共有多少人21. 如图①是图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂 ,灯罩 ,灯臂与底座构成的 . 可以绕点 上下调节一定的角度.使用发现:当 与水平线所成的角为30°时,台灯光线最佳.现测得点D到桌面的距离为 .请通过计算说明此时台灯光线是否为最佳?(参考数据: 取1.73).
(1)、本次调查随机抽取了 名学生:表中 ;(2)、补全条形统计图:(3)、若全校有2000名学生,请你估计该校掌握垃圾分类知识达到“优秀"和“良好”等级的学生共有多少人21. 如图①是图②是其侧面示意图(台灯底座高度忽略不计),其中灯臂 ,灯罩 ,灯臂与底座构成的 . 可以绕点 上下调节一定的角度.使用发现:当 与水平线所成的角为30°时,台灯光线最佳.现测得点D到桌面的距离为 .请通过计算说明此时台灯光线是否为最佳?(参考数据: 取1.73).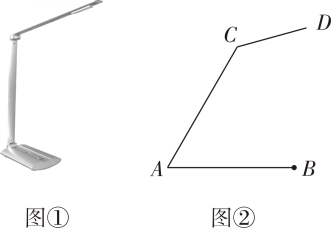 22. 如图,在矩形 中, 分别从 同时出发,分别沿边 移动,当有一个点先到达所在边的另一个端点时,其它各点也随之停止移动.已知移动段时间后,若 , .当x为何值时,以 为顶点的四边形是平行四边形?
22. 如图,在矩形 中, 分别从 同时出发,分别沿边 移动,当有一个点先到达所在边的另一个端点时,其它各点也随之停止移动.已知移动段时间后,若 , .当x为何值时,以 为顶点的四边形是平行四边形? 23. 从三角形(不是等腰三角形)一个顶点引出一条射线 与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
23. 从三角形(不是等腰三角形)一个顶点引出一条射线 与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线. (1)、如图1,在 中, 是 的完美分割线,且 , 则 的度数是(2)、如图2,在 中, 为角平分线, ,求证: 为 的完美分割线.(3)、如图2, 中, 是 的完美分割线,且 是以CD为底边的等腰三角形,求完美分割线CD的长.24. 如图,反比例函数 的图象经过点 ,射线 与反比例函数的图象的另一个交点为 ,射线 与x轴交于点E,与y轴交于点 轴, 垂足为D.
(1)、如图1,在 中, 是 的完美分割线,且 , 则 的度数是(2)、如图2,在 中, 为角平分线, ,求证: 为 的完美分割线.(3)、如图2, 中, 是 的完美分割线,且 是以CD为底边的等腰三角形,求完美分割线CD的长.24. 如图,反比例函数 的图象经过点 ,射线 与反比例函数的图象的另一个交点为 ,射线 与x轴交于点E,与y轴交于点 轴, 垂足为D. (1)、求反比例函数的解析式;(2)、求 的长(3)、在x轴上是否存在点P,使得 与 相似,若存在,请求出满足条件点P的坐标,若不存在,请说明理由.
(1)、求反比例函数的解析式;(2)、求 的长(3)、在x轴上是否存在点P,使得 与 相似,若存在,请求出满足条件点P的坐标,若不存在,请说明理由.