湖南省岳阳市平江县2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 已知反比例函数 $y = \frac{k}{x}$ 的图象经过点（2，－2），则k的值为

A、4 B、 $- \frac{1}{2}$ C、－4 D、－2

查看试题解析
2. 如图，在 $Δ A B C$ 中， $D E / / B C$ ， $A D = 9$ ， $D B = 3$ ， $C E = 2$ ，则 $A C$ 的长为（）

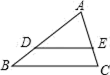A、6 B、7 C、8 D、9

查看试题解析
3. 若3x=2y（xy≠0），则下列比例式成立的是（　　）

A、 $\frac{x}{2} = \frac{y}{3}$ B、 $\frac{x}{3} = \frac{2}{y}$ C、 $\frac{x}{y} = \frac{3}{2}$ D、 $\frac{x}{3} = \frac{y}{2}$

查看试题解析
4. 若点 $A (- 3, y_{1})$ ， $B (- 2, y_{2})$ ， $C (1, y_{3})$ 都在反比例函数 $y = - \frac{12}{x}$ 的图象上，则 $y_{1}$ ， $y_{2}$ ， $y_{3}$ 的大小关系是（）

A、 $y_{2} < y_{1} < y_{3}$ B、 $y_{3} < y_{1} < y_{2}$ C、 $y_{1} < y_{2} < y_{3}$ D、 $y_{3} < y_{2} < y_{1}$

查看试题解析
5. 若将四根木条钉成的矩形木框变形为平行四边形ABCD的形状，并使其面积为矩形面积的一半，则这个平行四边形的一个最小内角为（）

A、30 B、45 C、60 D、90

查看试题解析
6. 方程 $x^{2} - 2 x - 3 = 0$ 变为 ${(x + a)}^{2} = b$ 的形式，正确的是（）

A、 ${(x + 1)}^{2} = 4$ B、 ${(x - 1)}^{2} = 4$ C、 ${(x + 1)}^{2} = 3$ D、 ${(x - 1)}^{2} = 3$

查看试题解析
7. 如图，在 $5 \times 4$ 的正方形网格中，每个小正方形的边长都是 $1$ ， $Δ A B C$ 的顶点都在这些小正方形的顶点上，则 $\sin ∠ B A C$ 的值为（）

A、 $\frac{4}{3}$ B、 $\frac{3}{4}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
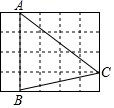8. 已知反比例函数 $y = \frac{k}{x}$ 的图象分别位于第二、第四象限， $A (x_{1}, y_{1})$ 、 $B (x_{2}, y_{2})$ 两点在该图象上，下列命题：①过点 $A$ 作 $A C ⊥ x$ 轴， $C$ 为垂足，连接 $O A$ .若 $Δ A C O$ 的面积为3，则 $k = - 6$ ；②若 $x_{1} < 0 < x_{2}$ ，则 $y_{1} > y_{2}$ ；③若 $x_{1} + x_{2} = 0$ ，则 $y_{1} + y_{2} = 0$ 其中真命题个数是（）

A、0 B、1 C、2 D、3

查看试题解析

二、填空题

9. 方程（x﹣1）（x+2）=0的解是．

查看试题解析
10. 已知在△ABC中，AB＝13，AC＝12，∠C＝90°，sinA＝．

查看试题解析
11. 为了了解某区初中学生的视力情况，随机抽取了该区500名初中学生进行调查.整理样本数据，得到下表：

视力

4.7以下

4.7

4.8

4.9

4.9以上

人数

102

98

80

93

127

根据抽样调查结果，估计该区12000名初中学生视力不低于4.8的人数是.

查看试题解析
12. 当m=时，函数 $y = (m + 1) x^{m^{2} - 2}$ 是反比例函数．

查看试题解析
13. 如图，在高2米，坡角为30°的楼梯表面铺地毯，地毯的长至少需米．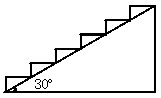

查看试题解析
14. 工人师傅给一幅长为120cm，宽为40cm的矩形书法作品装裱，作品的四周需要留白如图所示，已知左、右留白部分的宽度一样，上、下留白部分的宽度也一样，而且左侧留白部分的宽度是上面留白部分的宽度的2倍，使得装裱后整个挂图的面积为7000cm² ．设上面留白部分的宽度为xcm，可列得方程为。

查看试题解析
15. 矩形的两边长分别为 $x$ 和6（ $x < 6$ ），把它按如图方式分割成三个全等的小矩形，每一个小矩形与原矩形相似，则 $x =$ .

查看试题解析
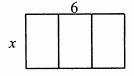16. 如图，若△ABC内一点P满足∠PAC=∠PCB=∠PBA，则称点P为△ABC的布罗卡尔点，三角形的布罗卡尔点是法国数学家和数学教育家克雷尔首次发现，后来被数学爱好者法国军官布罗卡尔重新发现，并用他的名字命名，布罗卡尔点的再次发现，引发了研究“三角形几何”的热潮．已知△ABC中，CA=CB，∠ACB=120°，P为△ABC的布罗卡尔点，若PA= $\sqrt{3}$ ，则PB+PC= ．

查看试题解析

三、解答题

17. 计算： ${(- 1)}^{2019} - \sqrt{12} + \tan 60 ° + {(π - 3.14)}^{0}$ ．

查看试题解析
18.
如图，四边形ABCD为菱形，M为BC上一点，连接AM交对角线BD于点G，并且∠ABM=2∠BAM．

(1)、求证：AG=BG；

(2)、若点M为BC的中点，同时S_△_BMG=1，求三角形ADG的面积．

查看试题解析
19. 已知关于x的方程x²+ax+a﹣2=0．

(1)、求证：不论a取何实数，该方程都有两个不相等的实数根；

(2)、若该方程的一个根为1，求a的值及该方程的另一根．

查看试题解析
20. 某高校学生会发现同学们就餐时剩余饭菜较多，浪费严重，于是准备在校内倡导“光盘行动”，让同学们珍惜粮食，为了让同学们理解这次活动的重要性，校学生会在某天午餐后，随机调查了部分同学就餐饭菜的剩余情况，并将结果统计后绘制成了如图所示的不完整的统计图．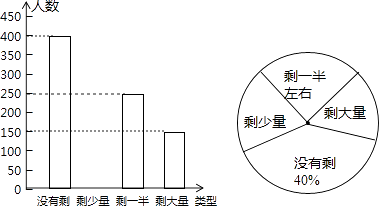

(1)、这次被调查的同学共有名；

(2)、补全条形统计图；

(3)、计算在扇形统计图中剩大量饭菜所对应扇形圆心角的度数；

(4)、校学生会通过数据分析，估计这次被调查的所有学生一餐浪费的食物可以供200人用一餐．据此估算，该校20000名学生一餐浪费的食物可供多少人食用一餐？

查看试题解析
21. 阳春三月，春暖花开，莲花山风景区游人如织，某摄影爱好者正在用无人机进行航拍.如图，在无人机镜头C处，观测风景区A处的俯角为30°，B处的俯角为45°，已知A，B两点之间的距离为200米，则无人机镜头C处的高度CD为多少？(点A，B，D在同一条直线上，结果保留根号)

查看试题解析
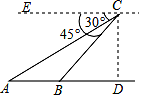22. 某商场销售一批衬衫，平均每天可销售出20件，每件盈利40元，为扩大销售盈利，商场决定采取适当的降价措施，但要求每件盈利不少于20元，经调查发现．若每件衬衫每降价1元，则商场每天可多销售2件．

(1)、若每件衬衫降价4元，则每天可盈利多少元？

(2)、若商场平均每天盈利1200元．则每件衬衫应降价多少元？

查看试题解析
23. 如图，一次函数y=kx+b与反比例函数 $y = \frac{k^{'}}{x}$ （x>0)的图象交于点A(a，3)和B(3，1）．

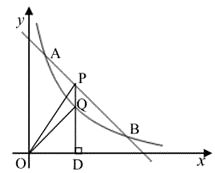(1)、求一次函数的解析式．

(2)、观察图象，写出反比例函数值小于一次函数值时x的取值范围．

(3)、点P是线段AB上一点，过点P作PD⊥x轴于点D，交反比例函数图象于点Q，连接OP、OQ，若△POQ的面积为 $\frac{1}{2}$ ，求P点的坐标。

查看试题解析
24. 如图，矩形ABCD中，∠ACB=30°，将一块直角三角板的直角顶点P放在两对角线AC，BD的交点处，以点P为旋转中心转动三角板，并保证三角板的两直角边分别于边AB，BC所在的直线相交，交点分别为E，F．

(1)、当PE⊥AB，PF⊥BC时，如图1，则 $\frac{PE}{PF}$ 的值为；

(2)、现将三角板绕点P逆时针旋转α（0°＜α＜60°）角，如图2，求 $\frac{PE}{PF}$ 的值；

(3)、在（2）的基础上继续旋转，当60°＜α＜90°，且使AP：PC=1：2时，如图3， $\frac{PE}{PF}$ 的值是否变化？证明你的结论．

查看试题解析

视力	4.7以下	4.7	4.8	4.9	4.9以上
人数	102	98	80	93	127