湖南省益阳市资阳区2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 以下是回收、绿色包装、节水、低碳四个标志，其中是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
2. 用配方法解一元二次方程 $x^{2} + 2 x - 1 = 0$ ，可将方程配方为（）

A、 ${(x + 1)}^{2} = 2$ B、 ${(x + 1)}^{2} = 0$ C、 ${(x - 1)}^{2} = 2$ D、 ${(x - 1)}^{2} = 0$

查看试题解析
3. 关于反比例函数y＝﹣ $\frac{3}{x}$ ，下列说法错误的是（　　）

A、图象经过点（1，﹣3） B、图象分布在第一、三象限 C、图象关于原点对称 D、图象与坐标轴没有交点

查看试题解析
4. 三角形在正方形网格纸中的位置如图所示，则 $\sin α$ 的值是（）

A、 $\frac{3}{5}$ B、 $\frac{3}{4}$ C、 $\frac{4}{3}$ D、 $\frac{4}{5}$

查看试题解析
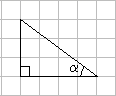5. 某专卖店专营某品牌女鞋，店主对上一周中不同尺码的鞋子销售情况统计如表：

尺码

35

36

37

38

39

平均每天销售数量（双）

2

8

10

6

2

该店主决定本周进货时，增加一些37码的女鞋，影响该店主决策的统计量是（　　）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析
6. 如图，四边形ABCD和四边形A'B'C'D'是以点O为位似中心的位似图形，若OA：OA'＝3：5，则四边形ABCD和四边形A'B'C'D'的面积比为（　　）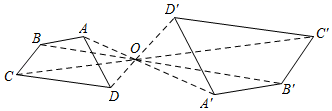

A、3：5 B、3：8 C、9：25 D、 $\sqrt{3}$ ： $\sqrt{5}$

查看试题解析
7. 在比例尺为1：1000000的地图上量得A ， B两地的距离是20cm ，那么A、B两地的实际距离是（　　）

A、2000000cm B、2000m C、200km D、2000km

查看试题解析
8. 某班同学要测量学校升国旗的旗杆的高度，在同一时刻，量得某一同学的身高是1.6m ，影长为1m ，旗杆的影长为7.5m ，则旗杆的高度是（　　）

A、9m B、10m C、11m D、12m

查看试题解析
9. 如图，在等边△ABC中，P为BC上一点，D为AC上一点，且∠APD＝60°，BP＝2，CD＝1，则△ABC的边长为（　　）

A、3 B、4 C、5 D、6

查看试题解析
10. 如图，在 $Δ A B C$ 中， $∠ A C B = 45^{°} ， B C = 1 ， A C = 2 \sqrt{2}$ ，将 $Δ A B C$ 绕点 $A$ 逆时针旋转得到 $Δ A B^{'} C^{'}$ ，其中点 $B'$ 与点 $B$ 是对应点，且点 $C ， B' ， C'$ 在同一条直线上；则 $B' C$ 的长为（）

A、 $3$ B、 $4$ C、 $2.5$ D、 $3 \sqrt{2}$

查看试题解析

二、填空题

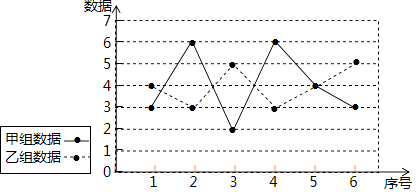
11. 一元二次方程的x²+2x﹣10＝0两根之和为．

查看试题解析
12. 经过点（1，﹣4）的反比例函数的解析式是．

查看试题解析
13. 计算sin60°cos60°的值为．

查看试题解析
14. 已知甲、乙两组数据的折线图如图，设甲、乙两组数据的方差分别为S_甲²、S_乙² ，则S_甲²S_乙²（填“＞”、“=”、“＜”）

查看试题解析
15. 如图，点D ， E分别在AB、AC上，且∠ABC＝∠AED ．若DE＝2，AE＝3，BC＝6，则AB的长为．

查看试题解析
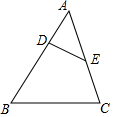16. 如图，E ， F分别为矩形ABCD的边AD ， BC的中点，且矩形ABCD与矩形EABF相似，AB＝1，则BC的长为．

查看试题解析
17. 反比例函数 $y = \frac{k}{x}$ 的图象上有一点P(2，n)，将点P向右平移1个单位，再向下平移1个单位得到点Q，若点Q也在该函数的图象上，则k＝．

查看试题解析
18. 找出如下图形变化的规律，则第100个图形中黑色正方形的数量是．

查看试题解析

三、解答题

19. 关于x的一元二次方程（k+1）x²﹣3x﹣3k﹣2＝0有一个根为﹣1，求k的值及方程的另一个根．

查看试题解析
20. 计算：2cos30°﹣2sin45°+3tan60°+|1﹣ $\sqrt{2}$ |．

查看试题解析

21. 先锋中学数学课题组为了了解初中学生阅读数学教科书的现状，随机抽取某校部分初中学生进行调查，调查结果分为“重视”、“一般”、“不重视”、“说不清楚”四种情况（依次用A、B、C、D表示），依据相关数据绘制成以下不完整的统计表和统计图，请根据图表中的信息解答下列问题：

类别	频数	频率
重视	a	0.25
一般	60	0.3
不重视	b	c
说不清楚	10	0.05

(1)、求样本容量及表格中a ， b ， c的值，并补全统计图；

(2)、若该校共有2000名学生，请估计该校“不重视阅读数学教科书”的学生人数．

查看试题解析

22. 如图，在平面直角坐标系中，过点M（0，2）的直线l与x轴平行，且直线l分别与反比例函数y＝ $\frac{6}{x}$ （x＞0）和y＝ $\frac{k}{x}$ （x＜0）的图象分别交于点P，Q.

(1)、求P点的坐标；

(2)、若△POQ的面积为9，求k的值.

查看试题解析
23. 如图，C城市在A城市正东方向，现计划在A、C两城市间修建一条高速铁路（即线段AC），经测量，森林保护区的中心P在城市A的北偏东60°方向上，在线段AC上距A城市150km的B处测得P在北偏东30°方向上，已知森林保护区是以点P为圆心，120km为半径的圆形区域，请问计划修建的这条高速铁路是否穿越保护区，为什么？（参考数据： $\sqrt{3}$ ≈1.732）

查看试题解析
24. 如图，某城建部门计划在新修的城市广场的一块长方形空地上修建一个面积为1200m²的停车场，将停车场四周余下的空地修建成同样宽的通道，已知长方形空地的长为50m ，宽为40m ．

(1)、求通道的宽度；

(2)、某公司希望用80万元的承包金额承揽修建广场的工程，城建部门认为金额太高需要降价，通过两次协商，最终以51.2万元达成一致，若两次降价的百分率相同，求每次降价的百分率．

查看试题解析
25. 如图，在等边△ABC中，把△ABC沿直线MN翻折，点A落在线段BC上的D点位置（D不与B、C重合），设∠AMN＝α．

(1)、用含α的代数式表示∠MDB和∠NDC ，并确定的α取值范围；

(2)、若α＝45°，求BD：DC的值；

(3)、求证：AM•CN＝AN•BD ．

查看试题解析
26. 如图，四边形OABC是矩形，A、C分别在y轴、x轴上，且OA＝6cm ， OC＝8cm ，点P从点A开始以2cm/s的速度向B运动，点Q从点B开始以1cm/s的速度向C运动，设运动时间为t ．

(1)、如图（1），当t为何值时，△BPQ的面积为4cm²？

(2)、当t为何值时，以B、P、Q为顶点的三角形与△ABC相似？

(3)、如图（2），在运动过程中的某一时刻，反比例函数y＝ $\frac{m}{x}$ 的图象恰好同时经过P、Q两点，求这个反比例函数的解析式．

查看试题解析

尺码	35	36	37	38	39
平均每天销售数量（双）	2	8	10	6	2