湖南省益阳市桃江县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. 点(4,-1)在反比例 的图象上,则下列各点在此函数图象上的是( )A、 B、 C、 D、2. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、3. 一元二次方程 的根的情况为( )A、有两个相等的实数根 B、只有一个实数根 C、有两个不相等的实数根 D、没有实数根4. 如图,以点O为位似中心,把 放大为原图形的2倍得到 ,若 与 的位似比为k,则以下结论中正确的是( )
 A、 B、 C、 D、5. 如图,在 中, , , 的垂直平分线 交 于点D,连接 ,若 ,则 的长是( )
A、 B、 C、 D、5. 如图,在 中, , , 的垂直平分线 交 于点D,连接 ,若 ,则 的长是( )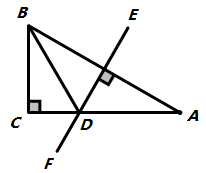 A、 B、 C、10 D、86. 如图,在 中,点D为 边上的一点,且 , 交 于D,过点D作 交 于点E,若 ,则 的面积为( )
A、 B、 C、10 D、86. 如图,在 中,点D为 边上的一点,且 , 交 于D,过点D作 交 于点E,若 ,则 的面积为( ) A、 B、4 C、 D、37. 下列说法错误的是( )A、在一定条件下,可能发生也可能不发生的事件称为随机事件 B、一组数据中出现次数最多的数据称为这组数据的众数 C、方差可以刻画数据的波动程度,方差越大,波动越小;方差越小,波动越大 D、全面调查和抽样调查是收集数据的两种方式8. 如图,抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中,错误的是( )
A、 B、4 C、 D、37. 下列说法错误的是( )A、在一定条件下,可能发生也可能不发生的事件称为随机事件 B、一组数据中出现次数最多的数据称为这组数据的众数 C、方差可以刻画数据的波动程度,方差越大,波动越小;方差越小,波动越大 D、全面调查和抽样调查是收集数据的两种方式8. 如图,抛物线y=ax2+bx+c的对称轴为直线x=1,则下列结论中,错误的是( )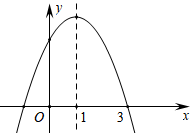 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
9. 一元二次方程 有一根为 ,则k的值为 .10. 如图,在平面直角坐标系中,点A的坐标为 ,反比例函数 的图象经过线段OA的中点B,则k= .
 11. 如图,人字梯AB,AC的长都为2米。当a=50°时,人字梯顶端高地面的高度AD是米(结果精确到0.1m。参考依据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19)
11. 如图,人字梯AB,AC的长都为2米。当a=50°时,人字梯顶端高地面的高度AD是米(结果精确到0.1m。参考依据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.19) 12. 如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: .
12. 如图所示,点E是平行四边形ABCD的边BC延长线上一点,连接AE,交CD于点F,连接BF.写出图中任意一对相似三角形: .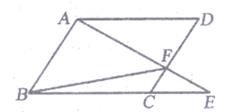 13. 平面直角坐标系中,二次函数 的图象的顶点坐标为 .14. 某地区九年级男生共有12000人,为了该地区九年级男生的身高情况,随机调查了其中100名男生的身高 ,并统计如下:
13. 平面直角坐标系中,二次函数 的图象的顶点坐标为 .14. 某地区九年级男生共有12000人,为了该地区九年级男生的身高情况,随机调查了其中100名男生的身高 ,并统计如下:组别
人数
5
38
42
15
根据以上结果,估计该地区九年级男生身高不低于170 的人数是.
三、解答题
-
15. 已知关于x的一元二次方程 有两个不相等的实数根 , .(1)、求k的取值范围;(2)、若 ,求k的值.16. 如图,在 中, , ,D是 边上的一点,且 , ,求 的长.
 17. 如图,公路某地段安装了一个测速仪器,检测点在公路上方10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知 , .(参考数据: , )
17. 如图,公路某地段安装了一个测速仪器,检测点在公路上方10m的A处,测得一辆汽车从B处行驶到C处所用时间为0.9秒,已知 , .(参考数据: , ) (1)、求B、C之间的距离;(2)、如果此地段限速为 ,那么这辆汽车是否超速?请说明理由.18. 2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解10—60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:
(1)、求B、C之间的距离;(2)、如果此地段限速为 ,那么这辆汽车是否超速?请说明理由.18. 2019年5月“亚洲文明对话大会”在北京成功举办,引起了世界人民的极大关注,某市一研究机构为了了解10—60岁年龄段市民对本次大会的关注程度,随机选取了100名年龄在该范围内的市民进行了调查,并将收集到的数据制成了如下尚不完整的频数分布表、频数分布走访图和扇形统计图:组别
年龄段
频数(人数)
第1组
10≤x<20
5
第2组
20≤x<30
a
第3组
30≤x<40
35
第4组
40≤x<50
20
第5组
50≤x<60
15
 (1)、请直接写出a、m的值及扇形统计图中第3组所对应的圆心角的度数;(2)、请补全上面的频数分布直方图;(3)、假设该市现有10—60岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少人?19. 2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.(1)、求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;(2)、若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?20. 如图,在平面直角坐标系 中,二次函数图象的顶点坐标为 ,该图象与 轴相交于点 、 ,与 轴相交于点 ,其中点 的横坐标为1.
(1)、请直接写出a、m的值及扇形统计图中第3组所对应的圆心角的度数;(2)、请补全上面的频数分布直方图;(3)、假设该市现有10—60岁的市民300万人,问第4组年龄段关注本次大会的人数经销商有多少人?19. 2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.(1)、求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;(2)、若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?20. 如图,在平面直角坐标系 中,二次函数图象的顶点坐标为 ,该图象与 轴相交于点 、 ,与 轴相交于点 ,其中点 的横坐标为1.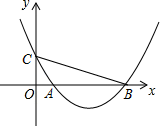 (1)、求该二次函数的表达式;(2)、求 .21. 如图, 为反比例函数 (x>0)图象上的一点,在 轴正半轴上有一点 , .连接 , ,且 .
(1)、求该二次函数的表达式;(2)、求 .21. 如图, 为反比例函数 (x>0)图象上的一点,在 轴正半轴上有一点 , .连接 , ,且 .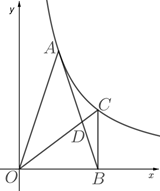 (1)、求 的值;(2)、过点 作 ,交反比例函数 (x>0)的图象于点 ,连接 交 于点 ,求 的值.22. 如图1,在等边 中, ,动点P从点A出发以 的速度沿 匀速运动,动点Q同时从点C出发以同样的速度沿 的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为 ,过点P作 于E, 交 边于D,线段 的中点为M,连接 .
(1)、求 的值;(2)、过点 作 ,交反比例函数 (x>0)的图象于点 ,连接 交 于点 ,求 的值.22. 如图1,在等边 中, ,动点P从点A出发以 的速度沿 匀速运动,动点Q同时从点C出发以同样的速度沿 的延长线方向匀速运动,当点P到达点B时,点P、Q同时停止运动.设运动时间为 ,过点P作 于E, 交 边于D,线段 的中点为M,连接 .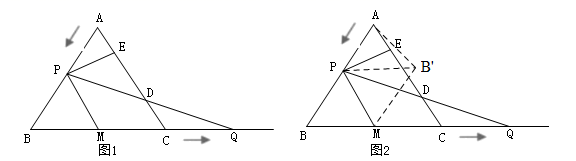 (1)、当t为何值时, 与 相似;(2)、在点P、Q运动过程中,点D、E也随之运动,线段 的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求 的长;(3)、如图2,将 沿直线 翻折,得 ,连接 ,当t为何值时, 的值最小?并求出最小值.
(1)、当t为何值时, 与 相似;(2)、在点P、Q运动过程中,点D、E也随之运动,线段 的长度是否会发生变化?若发生变化,请说明理由,若不发生变化,求 的长;(3)、如图2,将 沿直线 翻折,得 ,连接 ,当t为何值时, 的值最小?并求出最小值.