湖南省邵阳市双清区2019-2020学年九年级上学期期末数学试题
试卷更新日期：2020-12-22 类型：期末考试
一、单选题
-
1. 下列各点中，在反比例函数 图象上的是（ ）A、(3，1) B、（-3，1） C、(3， ) D、（ ，3）2. 已知函数 的图象过点(1，-2)，则该函数的图象必在（ ）
A、第二、三象限 B、第二、四象限 C、第一、三象限 D、第三、四象限3. 已知三角形的面积一定，则它底边a上的高h与底边a之间的函数关系的图象大致是（ ）A、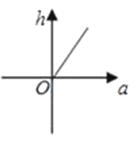
B、
C、
D、
4. 方程 是关于x的一元二次方程，则m的值不能是（ ）A、0 B、 C、 D、5.如图，在平行四边形ABCD中，EF∥AB交AD于E，交BD于F，DE：EA=3：4，EF=3，则CD的长为（ ）
A、4 B、7 C、3 D、126. 等腰三角形底边长为10㎝，周长为36cm，那么底角的余弦等于（ ）．A、 B、 C、 D、7. 如图所示，下列条件中能单独判断△ABC∽△ACD的个数是（ ）个．①∠ABC＝∠ACD；②∠ADC＝∠ACB；③ ＝ ；④AC2＝AD•AB
A、1 B、2 C、3 D、48. 如图，在一幅长 ，宽 的矩形风景画的四周镶一条金色纸边，制成一幅矩形图，如果要使整个挂图的面积是 ，设金色纸边的宽为 ，那么x满足的方程是（ ）
A、 B、 C、 D、9. 某农科院对甲、乙两种甜玉米各用10块相同条件的试验田进行试验，得到两个品种每公顷产量的两组数据，其方差分别为s甲2=0.002、s乙2=0.03，则（ ）A、甲比乙的产量稳定 B、乙比甲的产量稳定 C、甲、乙的产量一样稳定 D、无法确定哪一品种的产量更稳定10. 已知如图所示，在Rt△ABC中，∠A＝90°，∠BCA＝75°，AC＝8cm ， DE垂直平分BC ， 则BE的长是（ ）
A、4cm B、8cm C、16cm D、32cm二、填空题
-
11. 一个4米高的电线杆的影长是6米，它临近的一个建筑物的影长是36米．则这个建筑的高度是m．12. 已知 ，则 ．13. 如图，P是反比例函数y＝ 的图象上的一点，过点P分别作x轴、y轴的垂线，得图中阴影部分的面积为3，则这个反比例函数的比例系数是 ．
14. 方程 的根为.15.如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上．已知纸板的两条直角边DE=40cm，EF=20cm，测得边DF离地面的高度AC=1.5m，CD=8m，则树高AB=m.
16. 若关于 的一元二次方程x2+2x-k=0没有实数根，则k的取值范围是 ．17. △ABC与△A′B′C′是位似图形，且△ABC与△A′B′C′的位似比是1：2，已知△ABC的面积是3，则△A′B′C′的面积是.18. 某校开展“节约每一滴水”活动，为了了解开展活动一个月以来节约用水的情况，从八年级的400名同学中选取20名同学统计了各自家庭一个月节约用水情况如表，请你估计这400名同学的家庭一个月节约用水的总量大约是 ．节水量/m3
0.2
0.25
0.3
0.4
0.5
家庭数/个
2
4
6
7
1
三、解答题
-
19.(1)、x2﹣2x﹣3＝0(2)、cos45°•tan45°+ tan30°﹣2cos60°2sin45°20. 如图，∠AED =∠C，DE = 4，BC = 12，CD = 15，AD = 3，求AE、BE的长.
21. 某报社为了解市民对“社会主义核心价值观”的知晓程度，采取随机抽样的方式进行问卷调查，调查结果分为“A.非常了解”、“B.了解”、“C.基本了解”三个等级，并根据调查结果绘制了如下两幅不完整的统计图．
(1)、这次调查的市民人数为人，m＝ ， n＝；(2)、补全条形统计图；(3)、若该市约有市民100000人，请你根据抽样调查的结果，估计该市大约有多少人对“社会主义核心价值观”达到“A.非常了解”的程度．22. 如图，在△ABC中，∠C＝90°，DE⊥AB于E ， DF⊥BC于F ． 求证：△DEH∽△BCA ．
23. 如图，某测量工作人员与标杆顶端F、电视塔顶端在同一直线上，已知此人眼睛距地面1.5米，标杆为3米，且BC＝1米，CD＝6米，求电视塔的高ED ．
24. 某市百货商店服装部在销售中发现“米奇”童装平均每天可售出20件，每件获利40元．为了扩大销售，减少库存，增加利润，商场决定采取适当的降价措施，经过市场调查，发现如果每件童装每降价1元，则平均每天可多售出2件，要想平均每天在销售这种童装上获利1200元，那么每件童装应降价多少元？
