湖南省邵阳市隆回县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. 已知反比例函数 的图象在二、四象限,则m的取值范围是( )A、 B、 C、 D、2. 若关于x的方程 有两个相等的根,则k的值为( )A、10 B、10或14 C、-10或14 D、10或-143. 如图,在 中, 分别为 边上的中点,则 与 的面积之比是( )
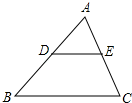 A、 B、 C、 D、4. 如图,在 中, , , ,则 的面积是( )
A、 B、 C、 D、4. 如图,在 中, , , ,则 的面积是( ) A、 B、 C、 D、5. 已知关于x的方程 ,若 ,则该方程一定有一个根为( )A、-1 B、0 C、1 D、1或-16. 池塘中放养了鲤鱼2000条,鲢鱼若干条,在几次随机捕捞中,共捕到鲤鱼200条,鲢鱼300条,估计池塘中原来放养了鲢鱼( )A、10000条 B、2000条 C、3000条 D、4000条7. 已知一斜坡的坡比为 ,坡长为26米,那么坡高为( )A、 米 B、 米 C、13米 D、 米8. 如图, 中, , , ,则 ( )
A、 B、 C、 D、5. 已知关于x的方程 ,若 ,则该方程一定有一个根为( )A、-1 B、0 C、1 D、1或-16. 池塘中放养了鲤鱼2000条,鲢鱼若干条,在几次随机捕捞中,共捕到鲤鱼200条,鲢鱼300条,估计池塘中原来放养了鲢鱼( )A、10000条 B、2000条 C、3000条 D、4000条7. 已知一斜坡的坡比为 ,坡长为26米,那么坡高为( )A、 米 B、 米 C、13米 D、 米8. 如图, 中, , , ,则 ( )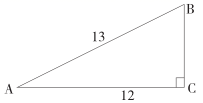 A、 B、 C、 D、9. 如图,在同一平面直角坐标系中,直线 与双曲线 相交于 两点,已知点A的坐标为 ,则点B的坐标为( )
A、 B、 C、 D、9. 如图,在同一平面直角坐标系中,直线 与双曲线 相交于 两点,已知点A的坐标为 ,则点B的坐标为( ) A、 B、 C、 D、10. 在 中, ,若已知 ,则 ( )A、 B、 C、 D、
A、 B、 C、 D、10. 在 中, ,若已知 ,则 ( )A、 B、 C、 D、二、填空题
-
11. 如果反比例函数的图象经过点 ,则该反比例函数的解析式为12. 关于x的方程 没有实数根,则k的取值范围为13. 已知线段a,b,c,d成比例线段,其中a=3cm,b=4cm,c=6cm,则d=cm;14. 甲、乙两同学在最近的5次数学测验中数学成绩的方差分别为 甲 , 乙 ,则数学成绩比较稳定的同学是15. 在 中, , , ,则16. 某校共1600名学生,为了解学生最喜欢的课外体育活动情况,学校随机抽查了200名学生,其中有92名学生表示喜欢的项目是跳绳,据此估计全校喜欢跳绳这项体育活动的学生有人.17. 如图,在 中, ,D为 边上一点,已知 , , ,则 .
 18. 如图,已知 中,点D、E、F分别是边 、 、 上的点,且 , ,且 ,若 ,那么
18. 如图,已知 中,点D、E、F分别是边 、 、 上的点,且 , ,且 ,若 ,那么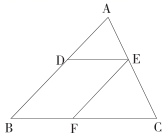 19. 如图, , 分别是 边 , 上的点, ,若 , , ,则 .
19. 如图, , 分别是 边 , 上的点, ,若 , , ,则 . 20. 若 、 是方程 的两个实数根,且x1+x2=1-x1 x2 , 则 m 的值为.
20. 若 、 是方程 的两个实数根,且x1+x2=1-x1 x2 , 则 m 的值为.三、解答题
-
21. 计算:(1)、(2)、解方程:22. 如图,已知 , , , , .
 (1)、求 和 的大小;(2)、求 的长23. 王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示.
(1)、求 和 的大小;(2)、求 的长23. 王大伯几年前承包了甲、乙两片荒山,各栽100棵杨梅树,成活98%.现已挂果,经济效益初步显现,为了分析收成情况,他分别从两山上随意各采摘了4棵树上的杨梅,每棵的产量如折线统计图所示. (1)、分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;(2)、试通过计算说明,哪个山上的杨梅产量较稳定?24. 如图,一次函数 的图象与反比例函数 的图象相交于点 , 两点,与x,y轴分别交于C,D两点.
(1)、分别计算甲、乙两山样本的平均数,并估算出甲、乙两山杨梅的产量总和;(2)、试通过计算说明,哪个山上的杨梅产量较稳定?24. 如图,一次函数 的图象与反比例函数 的图象相交于点 , 两点,与x,y轴分别交于C,D两点. (1)、求一次函数的表达式;(2)、求 的面积.25. 如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)、求一次函数的表达式;(2)、求 的面积.25. 如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=1: ,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.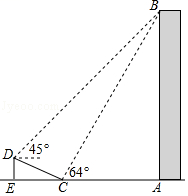 (1)、求斜坡CD的高度DE;(2)、求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).26. 如图,已知 是边长为 的等边三角形,动点P、Q同时从A、B两点出发,分别沿 、 方向匀速移动,它们的移动速度都是 ,当点P到达点B时,P、Q两点停止运动,设点P的运动时间的t秒,解答下列问题.
(1)、求斜坡CD的高度DE;(2)、求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).26. 如图,已知 是边长为 的等边三角形,动点P、Q同时从A、B两点出发,分别沿 、 方向匀速移动,它们的移动速度都是 ,当点P到达点B时,P、Q两点停止运动,设点P的运动时间的t秒,解答下列问题. (1)、 时,求 的面积;(2)、若 是直角三角形,求t的值;(3)、用t表示 的面积并判断 能否成立,若能成立,求t的值,若不能成立,说明理由.
(1)、 时,求 的面积;(2)、若 是直角三角形,求t的值;(3)、用t表示 的面积并判断 能否成立,若能成立,求t的值,若不能成立,说明理由.