湖南省娄底市新化县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. 已知点P(-1,4)在反比例函数 的图象上,则k的值是( )A、 B、 C、4 D、-42. 下列方程中不是一元二次方程的是( )A、 B、 C、 D、3. 下列图形中,是相似形的是( )A、所有平行四边形 B、所有矩形 C、所有菱形 D、所有正方形4. 点 关于x轴对称的点的坐标是( )A、 B、 C、 D、5. 下列说法,错误的是( )A、为了解一种灯泡的使用寿命,宜采用普查的方法 B、一组数据8,8,7,10,6,8,9的众数是8 C、方差反映了一组数据与其平均数的偏离程度 D、对于简单随机样本,可以用样本的方差去估计总体的方差6. 将抛物线 向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( ).A、 ; B、 ; C、 ; D、 .7. 用配方法解方程 时,配方结果正确的是( )A、 B、 C、 D、8. 如图,在 中, , ,则 的值是( )
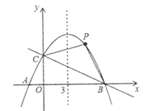
 A、 B、1 C、 D、9. 如图,直线y= x+3与x、y轴分别交于A、B两点,则cos∠BAO的值是( )
A、 B、1 C、 D、9. 如图,直线y= x+3与x、y轴分别交于A、B两点,则cos∠BAO的值是( ) A、 B、 C、 D、10. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、y的最小值为1 B、图象顶点坐标为 ,对称轴为直线 C、当 时,y的值随x值的增大而增大,当 时,y的值随x值的增大而减小 D、当 时,y的值随x值的增大而减小,当 时,y的值随x值的增大而增大11. 若关于x的一元二次方程 有实数根,则实数k的取值范围是( )A、 B、 C、 且 D、12. 对于一个函数,自变量x取a时,函数值y也等于a , 我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2 , 且x1<1<x2 , 则c的取值范围是( )A、c<﹣3 B、c<﹣2 C、c< D、c<1
A、 B、 C、 D、10. 在平面直角坐标系中,对于二次函数 ,下列说法中错误的是( )A、y的最小值为1 B、图象顶点坐标为 ,对称轴为直线 C、当 时,y的值随x值的增大而增大,当 时,y的值随x值的增大而减小 D、当 时,y的值随x值的增大而减小,当 时,y的值随x值的增大而增大11. 若关于x的一元二次方程 有实数根,则实数k的取值范围是( )A、 B、 C、 且 D、12. 对于一个函数,自变量x取a时,函数值y也等于a , 我们称a为这个函数的不动点.如果二次函数y=x2+2x+c有两个相异的不动点x1、x2 , 且x1<1<x2 , 则c的取值范围是( )A、c<﹣3 B、c<﹣2 C、c< D、c<1二、填空题
-
13. 一元二次方程 的根是 .14. 若 , , 是反比例函数 图象上的点,且 ,则 、 、 的大小关系是 .15. 某“中学生暑期环保小组”的同学,随机调查了“金沙绿岛”10户家庭一周内使用环保方便袋的数量,数据如下(单位:只):6,5,7,8,7,5,8,10,5,9,利用上述数据估计该小区500户家庭一周内需要环保方便袋只.16. 如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为.
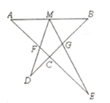
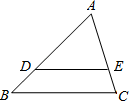
 17. 如图, , , 与 交于点G,则是相似三角形共有对.
17. 如图, , , 与 交于点G,则是相似三角形共有对. 18. 二次函数 的图象如图所示,若 , .则 、 的大小关系为 .(填“ ”、“ ”或“ ”)
18. 二次函数 的图象如图所示,若 , .则 、 的大小关系为 .(填“ ”、“ ”或“ ”)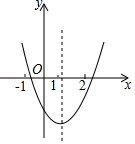
三、解答题
-
19. 计算:20. 已知关于x的一元二次方程 有两个不相等的实数根 , .(1)、若a为正整数,求a的值;(2)、若 , 满足 ,求a的值.21. 近年来,“在初中数学教学候总使用计算器是否直接影响学生计算能力的发展”这一问题受到了广泛关注,为此,某校随机调查了n名学生对此问题的看法(看法分为三种:没有影响,影响不大,影响很大),并将调查结果 绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
n名学生对使用计算器影响计算能力的发展看法人数统计表
看法
没有影响
影响不大
影响很大
学生人数(人)
40
60
m
 (1)、求n的值;(2)、统计表中的m=;(3)、估计该校1800名学生中认为“影响很大”的学生人数.22. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.
(1)、求n的值;(2)、统计表中的m=;(3)、估计该校1800名学生中认为“影响很大”的学生人数.22. 小李要外出参加“建国70周年”庆祝活动,需网购一个拉杆箱,图①,②分别是她上网时看到的某种型号拉杆箱的实物图与示意图,并获得了如下信息:滑杆 ,箱长 ,拉杆 的长度都相等, 在 上, 在 上,支杆 ,请根据以上信息,解决下列向题.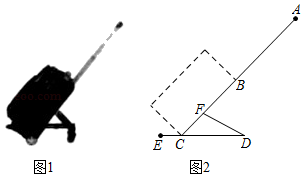 (1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).23. 2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.(1)、求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;(2)、若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?24. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C .
(1)、求 的长度(结果保留根号);(2)、求拉杆端点 到水平滑杆 的距离(结果保留根号).23. 2016年,某贫困户的家庭年人均纯收入为2500元,通过政府产业扶持,发展了养殖业后,到2018年,家庭年人均纯收入达到了3600元.(1)、求该贫困户2016年到2018年家庭年人均纯收入的年平均增长率;(2)、若年平均增长率保持不变,2019年该贫困户的家庭年人均纯收入是否能达到4200元?24. 如图,一次函数 的图象与反比例函数 在第一象限的图象交于 和B两点,与x轴交于点C .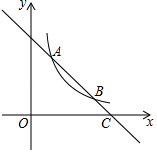 (1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.
(1)、求反比例函数的解析式;(2)、若点P在x轴上,且 的面积为5,求点P的坐标.