湖南省娄底市涟源市2019-2020学年九年级上学期数学期末试卷

试卷更新日期：2020-12-22 类型：期末考试

进入出卷网下载

一、单选题

1. 下面的函数是反比例函数的是（）

A、 $y = \frac{2}{x}$ B、 $y = x^{2} + 2 x$ C、 $y = \frac{x}{2}$ D、 $y = 3 x + 1$

查看试题解析
2. 若 $3 x = 7 y$ ( $x$ 、 $y$ 均不为0)，则下列等式成立的是（）

A、 $\frac{x}{3} = \frac{7}{y}$ B、 $\frac{y}{3} = \frac{7}{x}$ C、 $\frac{y}{x} = \frac{7}{3}$ D、 $\frac{x}{7} = \frac{y}{3}$

查看试题解析
3. 已知二次函数y＝ax²＋bx＋c(a≠0)的图象如图所示，当y＞0时，x的取值范围是（）

A、－1＜x＜2 B、x＞2 C、x＜－1 D、x＜－1或x＞2

查看试题解析
4. 如图，AB是⊙O直径，若∠AOC＝100°，则∠D的度数是（　　）

A、50° B、40° C、30° D、45°

查看试题解析
5. 下图中，最能清楚地显示每组数据在总数中所占百分比的统计图是（）

A、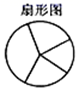 B、 C、 D、

查看试题解析
6. 已知关于 $x$ 的一元二次方程 $x^{2} - 4 x + c = 0$ 有两个相等的实数根，则 $c =$ （）

A、4 B、2 C、1 D、﹣4

查看试题解析
7. 若函数y＝（3﹣m） $x^{m^{2} - 7}$ ﹣x+1是二次函数，则m的值为（）

A、3 B、﹣3 C、±3 D、9

查看试题解析
8. 下列两个图形，一定相似的是（　　）

A、两个等腰三角形 B、两个直角三角形 C、两个等边三角形 D、两个矩形

查看试题解析
9. 如图，在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $\sin ∠ A = \frac{3}{4}$ ， $A B = 8 c m$ ，则 $△ A B C$ 的面积是（）

A、 $6 c m^{2}$ B、 $24 c m^{2}$ C、 $6 \sqrt{7} c m^{2}$ D、 $24 \sqrt{7} c m^{2}$

查看试题解析
10. 毕业前期，某班的全体学生互赠贺卡，共赠贺卡1980张.设某班共有 $x$ 名学生，那么所列方程为（）

A、 $\frac{1}{2} x (x + 1) = 1980$ B、 $\frac{1}{2} x (x - 1) = 1980$ C、 $x (x + 1) = 1980$ D、 $x (x - 1) = 1980$

查看试题解析
11. 赵州桥的桥拱可以用抛物线的一部分表示，函数关系为 $y = \frac{1}{25} x^{2}$ ，当水面宽度AB为20m时，水面与桥拱顶的高度DO等于（）

A、2m B、4m C、10m D、16m

查看试题解析
12. 如图，A、B两点在双曲线 $y = \frac{4}{x}$ 上，分别经过点A、B两点向x、y轴作垂线段，已知 $S_{阴影} =2$ ，则 $S_{1} + S_{2} =$ （）

A、6 B、5 C、4 D、3

查看试题解析

二、填空题

13. 若抛物线 $y = a x^{2} + b x + c$ 的开口向下，写出一个 $a$ 的可能值.

查看试题解析
14. 如图，Rt△ABC 中，∠C=90° ， AB=10， $\cos B = \frac{3}{5}$ ，则AC的长为 .

查看试题解析
15. 如图，在平面直角坐标系中，△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形，且点B(3，1)，B′(6，2)，若点A′(5，6)，则A的坐标为.

查看试题解析
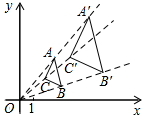16. 某校七年级共 $380$ 名学生参加数学测试，随机抽取 $50$ 名学生的成绩进行统计，其中 $20$ 名学生成绩达到优秀，估计该校七年级学生在这次数学测试中达到优秀的人数大约有人.

查看试题解析
17. 一定质量的二氧化碳，其体积V（m³）是密度ρ（kg/m³）的反比例函数，请你根据图中的已知条件，写出反比例函数的关系式，当V=1.9m³时，ρ= ．

查看试题解析
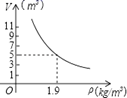18. 如图，△ABC是边长为2的等边三角形．取BC边中点E，作ED∥AB，EF∥AC，得到四边形EDAF，它的面积记作 $s_{1}$ ；取 $B E$ 中点 $E_{1}$ ，作 $E_{1} D_{1}$ ∥ $F B$ ， $E_{1} F_{1}$ ∥ $E F$ ，得到四边形 $E {}_{1}D_{1} F F_{1}$ ，它的面积记作 $s_{2}$ ．照此规律作下去，则 $s_{2019}$ = .

查看试题解析

三、解答题

19. 计算： $4 \sin 30^{°} - \sqrt{2} \cos 45^{°} - \sqrt{3} \tan 30^{°} + 2 \sin 60^{°}$

查看试题解析
20. 反比例函数 $y = \frac{k}{x}$ 与一次函数 $y = 2 x - 4$ 的图象都过 $A (m, 2)$ .

(1)、求A点坐标；

(2)、求反比例函数解析式.

查看试题解析
21. 一个不透明的布袋里装有3个白球，1个黑球和若干个红球，它们除颜色外其余都相同，从中任意摸出1个球，是白球的概率 $\frac{1}{2}$ .

(1)、布袋里红球有多少个？

(2)、先从布袋中摸出1个球后不放回，再摸出1个球，求出两次都摸到白球的概率.

查看试题解析
22. 为了测量山坡上的电线杆 $P Q$ 的高度，数学兴趣小组带上测角器和皮尺来到山脚下，他们在 $A$ 处测得信号塔顶端 $P$ 的仰角是 $45 °$ ，信号塔底端点 $Q$ 的仰角为 $30 °$ ，沿水平地面向前走100米到 $B$ 处，测得信号塔顶端 $P$ 的仰角是 $60 °$ ，求信号塔 $P Q$ 的高度.(结果保留整数)。

查看试题解析
23. 某公司今年1月份的生产成本是400万元，由于改进技术，生产成本逐月下降，3月份的生产成本是361万元．假设该公司2、3、4月每个月生产成本的下降率都相同．

(1)、求每个月生产成本的下降率；

(2)、请你预测4月份该公司的生产成本．

查看试题解析
24. 如图， $A B$ 为⊙ $O$ 的直径， $C$ 为⊙ $O$ 上一点， $D$ 为 $\hat{B C}$ 的中点.过点 $D$ 作直线 $A C$ 的垂线，垂足为 $E$ ，连接 $O D$ .

(1)、求证： $∠ A = ∠ D O B$ ；

(2)、 $D E$ 与⊙ $O$ 有怎样的位置关系？请说明理由.

查看试题解析
25. 如图， $R t △ A B C$ 中， $∠ A C B = 90 °$ ， $A C = B C$ ， $P$ 为 $△ A B C$ 内部一点，且 $∠ A P B = ∠ B P C = 135 °$ .

(1)、求证： $△ P A B ∽ △ P B C$ ；

(2)、求证： $P A = 2 P C$ .

查看试题解析
26. 如图，抛物线 $y = a x^{2} + b x + 2$ 交x轴于点 $A (- 3 ， 0)$ 和点 $B (1 ， 0)$ ，交y轴于点C.

(1)、求这个抛物线的函数表达式；

(2)、若点D的坐标为 $(- 1 ， 0)$ ，点P为第二象限内抛物线上的一个动点，求四边形 $A D C P$ 面积的最大值.

查看试题解析