湖南省凤凰县2019-2020学年九年级上学期数学期末试卷
试卷更新日期：2020-12-22 类型：期末考试
一、填空题
-
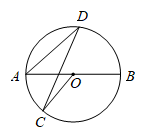
1. 方程x2﹣4＝0的解是 ．2. 数学试卷的选择题都是四选一的单项选择题，小阳对某道选择题完全不会做，只能靠猜测获得结果，则小阳做对的概率为.3. 已知扇形的面积为 ，圆心角为 ，则该扇形的半径为.4. 如图， 是⊙O的直径，C ， D是圆上两点，∠AOC＝50°，则∠D等于.
5. 在平面直角坐标系中，点 关于原点对称的点的坐标是.6. 抛物线 与x轴的公共点的个数是.7. 已知关于x的方程 （m﹣1） +2x﹣3=0是一元二次方程，则m的值为 ．8. 如图，⊙O的半径OA与弦BC交于点D ， 若OD=3，AD=2，BD=CD ， 则BC的长为.
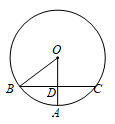
二、单选题
-
9. 已知 是方程 的一个根，则b的值为（ ）A、1 B、－1 C、 D、－210. 下列图形中，是轴对称图形但不是中心对称图形的是（ ）A、平行四边形 B、等边三角形 C、正方形 D、圆11. 正十二边形的每一个内角的度数为（ ）A、120° B、135° C、150° D、108°12.
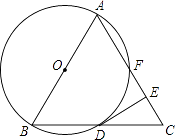
如图，四边形ABCD内接于⊙O，∠BCD=120°，则∠BAD的度数是（ ）
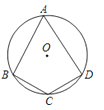A、30° B、60° C、80° D、120°13. 抛物线 的顶点坐标为（ ）A、 B、 C、 D、14. 用频率估计概率，可以发现，抛掷硬币，“正面朝上”的概率为0.5，那么掷一枚质地均匀的硬币10次，下列说法正确的是（ ）A、每两次必有1次正面向上 B、可能有5次正面向上 C、必有5次正面向上 D、不可能有10次正面向上15. 一元二次方程x2﹣2x+1=0的根的情况为（ ）A、有两个相等的实数根 B、有两个不相等的实数根 C、只有一个实数根 D、没有实数根16. 已知⊙O的半径为3cm，OP＝4cm，则点P与⊙O的位置关系是（ ）A、点P在圆内 B、点P在圆上 C、点P在圆外 D、无法确定17. 如图，将△ABC绕点A逆时针旋转100°，得到△ADE.若点D在线段BC的延长线上，则 的大小为（ ）
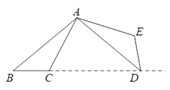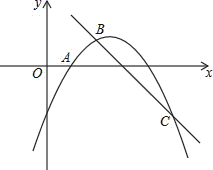
A、20° B、30° C、40° D、50°18. 已知二次函数y=ax2+bx+c的图象如图所示，则下列判断确的是（ ）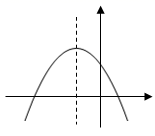
A、a＜0，b＞0，c＞0 B、a＜0，b＜0，c＜0 C、a＜0，b＜0，c＞0 D、a＞0，b＜0，c＞0三、解答题
-
19. 解方程： .20. 在平面直角坐标系内：
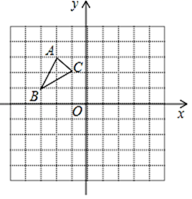
⑴作出△ABC关于原点对称的△A1B1C1 ， 并写出A1 ， B1 ， 的坐标.
⑵将△A1B1C1平移，使点A2的坐标为（－2，－4），作出△A2B2C2.
21. 汽车产业的发展，有效促进我国现代化建设.某汽车销售公司2016年盈利1500万元，到2018年盈利2160万元，且从2016年到2018年，每年盈利的年增长率相同.(1)、求每年盈利的年增长率；(2)、若该公司盈利的年增长率继续保持不变，那么2019年该公司盈利能否达到2500万元？22. 关于x的一元二次方程 有两个不相等的实数根.(1)、求m的取值范围；(2)、如果 是方程的一个根，求m的值及方程的另一个根.23. 已知二次函数y=x2﹣6x+5．(1)、将y=x2﹣6x+5化成y=a（x﹣h）2+k的形式；
(2)、求该二次函数的图象的对称轴和顶点坐标；(3)、当x取何值时，y随x的增大而减小．24. 有A、B两组卡片共5张，A组的三张分别写有数字2，4，6，B组的两张分别写有3，5．它们除了数字外没有任何区别，(1)、随机从A组抽取一张，求抽到数字为2的概率；(2)、随机地分别从A组、B组各抽取一张，请你用列表或画树状图的方法表示所有等可能的结果.现制定这样一个游戏规则：若选出的两数之积为3的倍数，则甲获胜；否则乙获胜．请问这样的游戏规则对甲乙双方公平吗？为什么？
