湖南省常德市澧县2019-2020学年九年级上学期数学期末试卷
试卷更新日期:2020-12-22 类型:期末考试
一、单选题
-
1. 下列各式中 , 均不为 , 和 成反比例关系的是( )A、 B、 C、 D、2. 已知⊙O的半径为5,若PO=4,则点P与⊙O的位置关系是( )A、点P在⊙O内 B、点P在⊙O上 C、点P在⊙O外 D、无法判断3. 下列方程中,是一元二次方程的是( )A、 B、 C、 D、4. 在 中, , , ,则 的值为( )A、 B、 C、 D、5. 已知抛物线y=﹣x2+4x+3,则该抛物线的顶点坐标为( )A、(﹣2,7) B、(2,7) C、(2,﹣9) D、(﹣2,﹣9)6. 以下A、B、C、D四个三角形中,与左图中的三角形相似的是( )
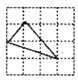 A、
A、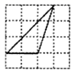 B、
B、 C、
C、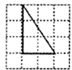 D、
D、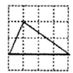 7. 若二次函数 的图像与 轴有两个交点,则实数 的取值范围是( )A、 B、 C、 D、8. 如图,A,B是反比例函数y= 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )
7. 若二次函数 的图像与 轴有两个交点,则实数 的取值范围是( )A、 B、 C、 D、8. 如图,A,B是反比例函数y= 在第一象限内的图象上的两点,且A,B两点的横坐标分别是2和4,则△OAB的面积是( )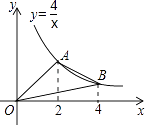 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
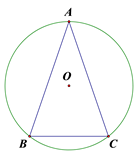
9. 如图,在⊙O中, ,AB=3,则AC=.
 10. 若关于x的一元二次方程 没有实数根,则k的取值范围是 .11. .12. 如图,在 中, 交 于点D,交 于点E.若 、 、 ,则 的长为 .
10. 若关于x的一元二次方程 没有实数根,则k的取值范围是 .11. .12. 如图,在 中, 交 于点D,交 于点E.若 、 、 ,则 的长为 .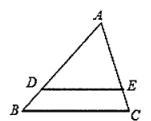 13. 已知 ∽ ,若周长比为4:9,则 .14. 为了对1000件某品牌衬衣进行抽检,统计合格衬衣的件数,在相同条件下,经过大量的重复抽检,发现一件合格衬衣的频率稳定在常数0.98附近,由此可估计这1000件中不合格的衬衣约为件.15. 如果函数 是关于 的二次函数,则 .16. 如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数 的图象经过点B,则k的值是 .
13. 已知 ∽ ,若周长比为4:9,则 .14. 为了对1000件某品牌衬衣进行抽检,统计合格衬衣的件数,在相同条件下,经过大量的重复抽检,发现一件合格衬衣的频率稳定在常数0.98附近,由此可估计这1000件中不合格的衬衣约为件.15. 如果函数 是关于 的二次函数,则 .16. 如图,点A的坐标是(2,0),△ABO是等边三角形,点B在第一象限,若反比例函数 的图象经过点B,则k的值是 .
三、解答题
-
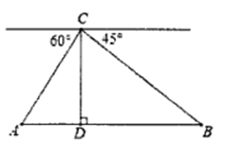
17. 如图,无人机在空中C处测得地面A、B两点的俯角分别为60〫、45〫,如果无人机距地面高度 米,点A、D、B在同水平直线上,求A、B两点间的距离.(结果保留根号)
 18. 已知:二次函数 ,求证:无论m为任何实数,该二次函数的图象与x轴都在两个交点;19. 蓄电池的电压为定值,使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示.
18. 已知:二次函数 ,求证:无论m为任何实数,该二次函数的图象与x轴都在两个交点;19. 蓄电池的电压为定值,使用此电源时,电流I(A)是电阻R(Ω)的反比例函数,其图象如图所示.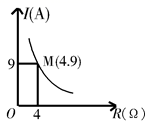 (1)、求这个反比例函数的表达式;(2)、当R=10Ω时,求电流I(A).20. 如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)
(1)、求这个反比例函数的表达式;(2)、当R=10Ω时,求电流I(A).20. 如图,是一张盾构隧道断面结构图.隧道内部为以O为圆心,AB为直径的圆.隧道内部共分为三层,上层为排烟道,中间为行车隧道,下层为服务层.点A到顶棚的距离为1.6m,顶棚到路面的距离是6.4m,点B到路面的距离为4.0m.请求出路面CD的宽度.(精确到0.1m)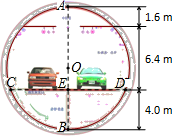 21. 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题:
21. 为推进“全国亿万学生阳光体育运动”的实施,组织广大同学开展健康向上的第二课堂活动.我市某中学准备组建球类社团(足球、篮球、羽毛球、乒乓球)、舞蹈社团、健美操社团、武术社团,为了解在校学生对这4个社团活动的喜爱情况,该校随机抽取部分初中生进行了“你最喜欢哪个社团”调查,依据相关数据绘制成以下不完整的统计表,请根据图表中的信息解答下列问题: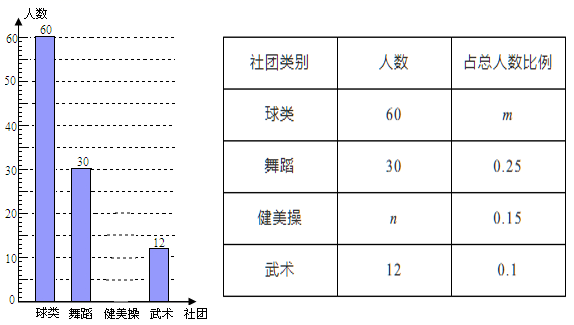 (1)、求样本容量及表格中m、n的值;(2)、请补全统计图;(3)、被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数.22. 已知二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),C(0,3).
(1)、求样本容量及表格中m、n的值;(2)、请补全统计图;(3)、被调查的60个喜欢球类同学中有3人最喜欢足球,若该校有3000名学生,请估计该校最喜欢足球的人数.22. 已知二次函数y=﹣x2+bx+c的图象经过点A(﹣1,0),C(0,3).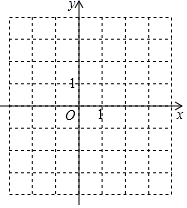 (1)、求二次函数的解析式;(2)、在图中,画出二次函数的图象;(3)、根据图象,直接写出当y≤0时,x的取值范围.23. 某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为 万元/辆,经销一段时间后发现:当该型号汽车售价定为 万元/辆时,平均每周售出 辆;售价每降低 万元,平均每周多售出 辆.(1)、当售价为 万元/辆时,平均每周的销售利润为万元;(2)、若该店计划平均每周的销售利润是 万元,为了尽快减少库存,求每辆汽车的售价.24. 在平面直角坐标系中,一次函数 (a≠0)的图象与反比例函数 的图象交于第二、第四象限内的A、B两点,与 轴交于点C,过点A作AH⊥ 轴,垂足为点H,OH=3,tan∠AOH= ,点B的坐标为( ,-2).
(1)、求二次函数的解析式;(2)、在图中,画出二次函数的图象;(3)、根据图象,直接写出当y≤0时,x的取值范围.23. 某汽车专卖店经销某种型号的汽车.已知该型号汽车的进价为 万元/辆,经销一段时间后发现:当该型号汽车售价定为 万元/辆时,平均每周售出 辆;售价每降低 万元,平均每周多售出 辆.(1)、当售价为 万元/辆时,平均每周的销售利润为万元;(2)、若该店计划平均每周的销售利润是 万元,为了尽快减少库存,求每辆汽车的售价.24. 在平面直角坐标系中,一次函数 (a≠0)的图象与反比例函数 的图象交于第二、第四象限内的A、B两点,与 轴交于点C,过点A作AH⊥ 轴,垂足为点H,OH=3,tan∠AOH= ,点B的坐标为( ,-2).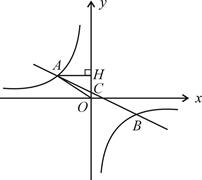 (1)、求该反比例函数和一次函数的解析式;(2)、求△AHO的周长.25. 在平面直角坐标系中,抛物线 与x轴的两个交点分别是 、 ,C为顶点.
(1)、求该反比例函数和一次函数的解析式;(2)、求△AHO的周长.25. 在平面直角坐标系中,抛物线 与x轴的两个交点分别是 、 ,C为顶点.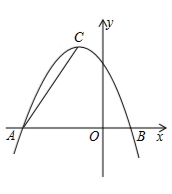 (1)、求m、n的值和顶点C的坐标;(2)、在y轴上是否存在点D,使得 是以 为斜边的直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.26. 定义:
(1)、求m、n的值和顶点C的坐标;(2)、在y轴上是否存在点D,使得 是以 为斜边的直角三角形?若存在,求出点D的坐标;若不存在,请说明理由.26. 定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:
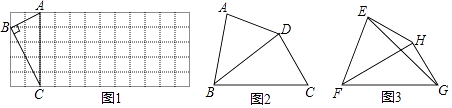 (1)、如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);(2)、如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.
(1)、如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);(2)、如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”;
(3)、如图3,已知FH是四边形EFCH的“相似对角线”,∠EFH=∠HFG=30°,连接EG,若△EFG的面积为2 ,求FH的长.