初中数学人教版九年级下学期同步测试 26.2 实际问题与反比例函数

试卷更新日期：2020-12-21 类型：同步测试

进入出卷网下载

一、单选题

1. 某气球内充满了一定质量的气体，在温度不变的条件下，气球内气体的压强p(Pa)是气球体积V(m³)的反比例函数，且当V=1.5m³时，p=16000Pa，当气球内的气压大于40000Pa时，气球将爆炸，为确保气球不爆炸，气球的体积应(　　)

A、不小于0.5m³ B、不大于0.5m³ C、不小于0.6m³ D、不大于0.6m³

查看试题解析
2. 如图，曲线表示温度T（℃）与时间t（h）之间的函数关系，它是一个反比例函数的图象的一支.当温度T≤2℃时，时间t应（）

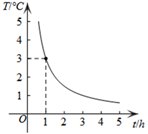A、不小于 $\frac{2}{3}$ h B、不大于 $\frac{2}{3}$ h C、不小于 $\frac{3}{2}$ h D、不大于 $\frac{3}{2}$ h

查看试题解析
3. 如图，在某温度不变的条件下，通过一次又一次地对气缸顶部的活塞加压，测出每一次加压后气缸内气体的体积 $V (mL)$ 与气体对气缸壁产生的压强 $P (kPa)$ 的关系可以用如图所示的函数图象进行表示，下列说法正确的是（）

A、气压P与体积V的关系式为 $P = k V (k > 0)$ B、当气压 $P = 70$ 时，体积V的取值范围为 $70<V<80$ C、当体积V变为原来的一半时，对应的气压P也变为原来的一半 D、当 $60 ⩽ V ⩽ 100$ 时，气压P随着体积V的增大而减小

查看试题解析
4. 一司机驾驶汽车从甲地去乙地，他以80千米/时的平均速度用了6小时到达目的地，当他按原路匀速返回时，汽车的速度v（千米/时）与时间t（小时）的函数关系为（　　）

A、v＝ $\frac{480}{t}$ B、v+t＝480 C、v＝ $\frac{80}{t}$ D、v＝ $\frac{t - 6}{t}$

查看试题解析
5. 已知圆锥的侧面积是100πcm²，若圆锥底面半径为rcm，母线长为1cm，则l关于r的函数的图象大致是（）

A、 B、 C、 D、

查看试题解析
6. 已知蓄电池的电压U为定值，使用蓄电池时，电流I（单位：A）与电阻R（单位：Ω）是反比例函数关系，它的图象如图所示.若此蓄电池为某用电器的电源，限制电流不能超过12A，那么用电器的可变电阻R应控制在什么范围？（）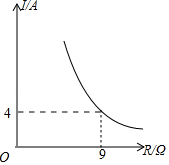

A、R≥3Ω B、R≤3Ω C、R≥12Ω D、R≥24Ω

查看试题解析
7. 如图，已知点A在反比例函数 $y = \frac{2}{x}$ 的图象上，点B，C分别在反比例函数 $y = \frac{4}{x}$ 的图象上，且AB∥x轴，AC∥y轴，若AB=2AC，则点A的坐标为（）

A、（1，2） B、（2，1） C、（ $\sqrt{2}$ ， $\sqrt{2}$ ） D、（3， $\frac{2}{3}$ ）

查看试题解析
8. 一个圆柱的侧面展开图是一个面积为10的矩形，这个圆柱的高为L与这个圆柱的底面半径r之间的函数关系为（）

A、正比例函数 B、反比例函数 C、一次函数 D、二次函数

查看试题解析
9. 如图，慢慢将电线杆竖起，如果所用力F的方向始终竖直向上，则电线杆竖起过程中所用力的大小将（）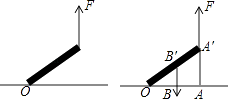

A、变大 B、变小 C、不变 D、无法判断

查看试题解析
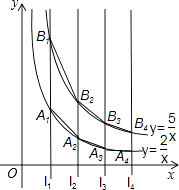
10.
如图，直线l₁：x=1，l₂：x=2，l₃：x=3，l₄：x=4，…，与函数y= $\frac{2}{x}$ （x＞0）的图象分别交于点A₁、A₂、A₃、A₄、…；与函数y= $\frac{5}{x} (x > 0)$ 的图象分别交于点B₁、B₂、B₃、B₄、…．如果四边形A₁A₂B₂B₁的面积记为S₁ ，四边形A₂A₃B₃B₂的面积记为S₂ ，四边形A₃A₄B₄B₃的面积记为S₃ ， …，以此类推．则S₁₀的值是（　　）

A、 $\frac{19}{60}$ B、 $\frac{23}{88}$ C、 $\frac{25}{104}$ D、 $\frac{63}{220}$

查看试题解析

二、填空题

11. 经济学家在硏究市场供求关系时，一般用纵轴表示产品单价（自变量），而用横轴表示产品数量（因变量），下列两条曲线分别表示某种产品数量与单价之间的供求关系，一条表示厂商希望的供应曲线，另一条表示客户希望的需求曲线，其中表示客户希望的需求曲线的是（填入序号即可）．

查看试题解析
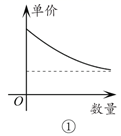
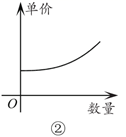12. 某产品的进价为50元，该产品的日销量 $y$ （件）是日销价 $x$ （元）的反比例函数，且当售价为每件100元时，每日可售出40件，为获得日利润为1500元，售价应定为.

查看试题解析
13. 某水池容积为300m³ ，原有水100m³ ，现以xm³／min的速度匀速向水池中注水，注满水需要y min，则y关于x的函数表达式为．

查看试题解析
14. 如图，已知点A在反比例函数 $y = \frac{k}{x} (x < 0)$ 上，作Rt△ABC ，使边BC在x轴上且∠ABC＝90°，点D在AC上且CD＝2AD ，连DB并延长交y轴于点E ，若△BCE的面积为8，△ABC的面积为3，则k＝．

查看试题解析
15.
如图，M为双曲线y= $\frac{\sqrt{3}}{x}$ 上的一点，过点M作x轴、y轴的垂线，分别交直线y=﹣x+m于点D、C两点，若直线y=﹣x+m与y轴交于点A，与x轴相交于点B，则AD•BC的值为．

查看试题解析
16.
如图，四边形OABC是矩形，ADEF是正方形，点A、D在x轴的正半轴上，点C在y轴的正半轴上，点F在AB上，点B、E在反比例函数y= $\frac{k}{x}$ 的图象上，OA=1，OC=6，则正方形ADEF的边长为．

查看试题解析

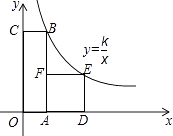
三、解答题

17. 方方驾驶小汽车匀速地从A地行使到B地，行驶里程为480千米，设小汽车的行使时间为t（单位：小时），行使速度为v（单位：千米/小时），且全程速度限定为不超过120千米/小时.

(1)、求v关于t的函数表达式；

(2)、方方上午8点驾驶小汽车从A出发.
①方方需在当天12点48分至14点（含12点48分和14点）间到达B地，求小汽车行驶速度v的范围.

②方方能否在当天11点30分前到达B地？说明理由.

查看试题解析
18. 小明在某一次实验中，测得两个变量之间的关系如下表所示：
x
1
2
3
4

12
y
12.03
5.98

3.03
1.99
1.00
请你根据表格回答下列问题：
①这两个变量之间可能是怎样的函数关系？你是怎样作出判断的？请你简要说明理由；
②请你写出这个函数的解析式；
③表格中空缺的数值可能是多少？请你给出合理的数值．

查看试题解析
19. 某电器商场销售甲、乙两种品牌空调，已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20％，用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台．

(1)、求甲、乙两种品牌空调的进货价；

(2)、该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售，其中甲种品牌空调的售价为2500元／台，乙种品牌空调的售价为3500元／台．请您帮该商场设计一种进货方案，使得在售完这10台空调后获利最大，并求出最大利润．

查看试题解析
20. 某市为促进经济发展，增强对外贸易的竞争力，把距离港口360千米的普通公路升级成了同等长度的高速公路，结果汽车行驶的平均速度比原来提高了50%，行驶时间缩短了2小时，求汽车原来的平均速度.

查看试题解析
21.
如图，一次函数y=kx+b的图象与反比例函数y= $\frac{m}{x}$ （x＞0）的图象交于P（n，2），与x轴交于A（﹣4，0），与y轴交于C，PB⊥x轴于点B，且AC=BC．
（1）求一次函数、反比例函数的解析式；
（2）反比例函数图象有一点D，使得以B、C、P、D为顶点的四边形是菱形，求出点D的坐标．

查看试题解析
22. 某物流公司要把3000吨货物从M市运到W市．（每日的运输量为固定值）
（1）从运输开始，每天运输的货物吨数y（单位：吨）与运输时间x（单位：天）之间有怎样的函数关系式？
（2）因受到沿线道路改扩建工程影响，实际每天的运输量比原计划少20%，以致推迟1天完成运输任务，求原计划完成运输任务的天数．

查看试题解析

四、综合题

23. 小阳要把一篇文章录入电脑，所需时间y（分）与录入文字的速度x（字/分）之间的反比例函数关系如图．

(1)、这篇文章共有多少个字？

(2)、写出y与x的函数表达式；

(3)、若小阳7点20分开始录入，预计完成时间不超过7点28分，请你用函数的性质说明小阳录入文字的速度至少为多少？

查看试题解析
24. 某游泳池毎次换水前后水的体积基本保持不变，当该游泳池以每小时300立方米的速度放水时，经3小时能将池内的水放完．设放水的速度为x立方米/时，将池内的水放完需y小时．已知该游泳池毎小时的最大放水速度为350立方米

(1)、求y关于x的函数表达式．

(2)、若该游泳池将放水速度控制在每小时200立方米至250立方米（含200立方米和250立方米），求放水时间y的范围．

(3)、该游泳池能否在2.5小时内将池内的水放完？请说明理由．

查看试题解析

x	1	2	3	4		12
y	12.03	5.98		3.03	1.99	1.00