浙江省2020-2021年九年级上学期数学期末测试模拟卷A卷
试卷更新日期:2020-12-21 类型:期末考试
一、单选题
-
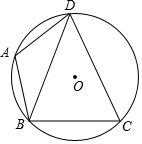
1. 将二次函数y=(x﹣1)2+2的图象向上平移3个单位长度,得到的拋物线相应的函数表达式为( )A、y=(x+2)2﹣2 B、y=(x﹣4)2+2 C、y=(x﹣1)2﹣1 D、y=(x﹣1)2+52. 以原点为中心,将点P(4,5)按逆时针方向旋转90°,得到的点Q所在的象限为( )A、第一象限 B、第二象限 C、第三象限 D、第四象限3. 下列事件中是不可能事件的是( )A、守株待兔 B、瓮中捉鳖 C、水中捞月 D、百步穿杨4. 在一个不透明的袋子里装有红球、黄球共 个,这些球除颜色外都相同.小明通过多次实验发现,摸出红球的频率稳定在 左右,则袋子中红球的个数最有可能是( )A、5 B、10 C、12 D、155. 如图,四边形ABCD是⊙O的内接四边形,AB=AD,若∠C=68°,则∠ABD的度数为( )
 A、34° B、56° C、68° D、112°6. 竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为( )A、 B、 C、 D、7. 正六边形的周长为12,则它的面积为( )A、 B、 C、 D、8. 函数y=kx﹣3与y=
A、34° B、56° C、68° D、112°6. 竖直上抛物体离地面的高度 与运动时间 之间的关系可以近似地用公式 表示,其中 是物体抛出时离地面的高度, 是物体抛出时的速度.某人将一个小球从距地面 的高处以 的速度竖直向上抛出,小球达到的离地面的最大高度为( )A、 B、 C、 D、7. 正六边形的周长为12,则它的面积为( )A、 B、 C、 D、8. 函数y=kx﹣3与y= (k≠0)在同一坐标系内的图象可能是( ) A、
(k≠0)在同一坐标系内的图象可能是( ) A、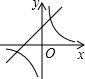 B、
B、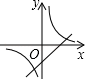 C、
C、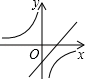 D、
D、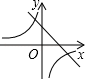 9. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )
9. 如图,抛物线 的对称轴是 .下列结论:① ;② ;③ ;④ ,正确的有( )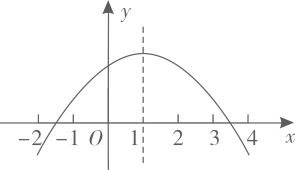 A、4个 B、3个 C、2个 D、1个10. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )
A、4个 B、3个 C、2个 D、1个10. 古希腊数学家欧多克索斯在深入研究比例理论时,提出了分线段的“中末比”问题:点G将一线段 分为两线段 , ,使得其中较长的一段 是全长 与较短的段 的比例中项,即满足 ,后人把 这个数称为“黄金分割”数,把点G称为线段 的“黄金分割”点.如图,在 中,已知 , ,若D , E是边 的两个“黄金分割”点,则 的面积为( )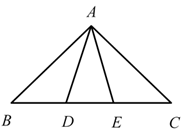 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 若 , ,则 与 的比例中项为.12. 如图,在⊙O 中,弧AB=弧AC,∠A=30°,则∠B=°.
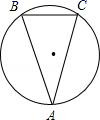 13. 如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上,那么△ABC的外接圆半径是.
13. 如图,网格的小正方形的边长均为1,小正方形的顶点叫做格点.△ABC的三个顶点都在格点上,那么△ABC的外接圆半径是.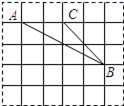 14. 直线CD∥EF,若OC=3,CE=4,则 的值是 .
14. 直线CD∥EF,若OC=3,CE=4,则 的值是 .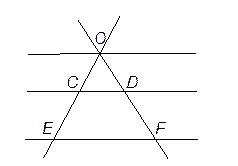 15. 如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是.
15. 如图是一圆形水管的截面图,已知⊙O的半径OA=13,水面宽AB=24,则水的深度CD是. 16. 一张等腰三角形纸片,底边长为 ,底边上的高长 .现沿底边依次从下往上数剪宽度均为 的矩形纸条,如图所示,已知剪得纸条中有一张是正方形,则这张正方形纸条是第张
16. 一张等腰三角形纸片,底边长为 ,底边上的高长 .现沿底边依次从下往上数剪宽度均为 的矩形纸条,如图所示,已知剪得纸条中有一张是正方形,则这张正方形纸条是第张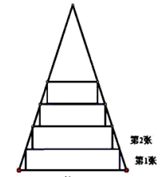
三、综合题
-
17. 已知函数 是二次函数.(1)、求m的值;(2)、求这个二次函数的解析式,并指出开口方向、对称轴和顶点坐标.18. 节假日期间、某商场组织游戏,主持人请三位家长分别带自己的孩于参加游戏,A、B、C分别表示一位家长,他们的孩子分别对应的是a,b, 若主持人分别从三位家长和三位孩子中各选一人参加游戏.(1)、若已选中家长A,则恰好选中自己孩子的概率是.(2)、请用画树状图或列表法求出被选中的恰好是同一家庭成员的概率.19. 一条隧道的横截面如图所示,它的上部是一个半圆,下部是一个矩形,矩形的一边长为 米.如果隧道下部的宽度大于 米但不超过 米,求隧道横截面积 (平方米)关于上部半圆半径 (米)的函数解析式及函数的定义域.
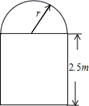 20. 如图,在 网格图中,每个小正方形边长均为 ,点 和四边形 的顶点均在小正方形的顶点上.
20. 如图,在 网格图中,每个小正方形边长均为 ,点 和四边形 的顶点均在小正方形的顶点上.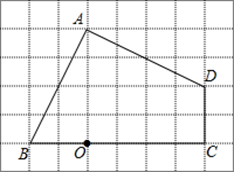 (1)、以 为位似中心,在网格图中作四边形 和四边形 位似,且位似比为 ;(2)、根据(1)填空: .21. 如图,BD为⊙O的直径,弦AB、CD相交于点P,且AB=CD。
(1)、以 为位似中心,在网格图中作四边形 和四边形 位似,且位似比为 ;(2)、根据(1)填空: .21. 如图,BD为⊙O的直径,弦AB、CD相交于点P,且AB=CD。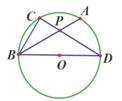 (1)、求证:∠ABD=∠CDB。(2)、连结BC,若AB平分∠CBD,求 的度数。22. 如图, 是一块锐角三角形余料,其中 ,高 ,现在要把它裁成一块正方形材料备用,使正方形的一边 在 上,其余两个顶点 , 分别在 , 上,问这块正方形材料的边长是多少?
(1)、求证:∠ABD=∠CDB。(2)、连结BC,若AB平分∠CBD,求 的度数。22. 如图, 是一块锐角三角形余料,其中 ,高 ,现在要把它裁成一块正方形材料备用,使正方形的一边 在 上,其余两个顶点 , 分别在 , 上,问这块正方形材料的边长是多少? 23. “新冠肺炎”疫情期间某工厂为支持国家抗击疫情每天连夜生产急缺的消毒液,已知每瓶消毒液的生产成本为20元,为了合理定价,根据市场调查发现,当销售单价为30元时,每天的销售量为6000瓶,若销售单价每降低1元,则每天能多销售1000瓶,但要求销售单价不能低于成本且不高于30元.(1)、求每天的销售量 (瓶)与销售单价 (元)之间的函数关系式;(2)、求每天的利润 (元)与销售单价 (元)之间的函数关系式;(3)、该工厂负责人决定将每天的利润全部捐献出来进一步支持国家抗击“新冠肺炎”疫情,则当销售单价为多少元时,每天的销售利润最大?最大利润是多少?24. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C(0,3),且抛物线的顶点坐标为(1,4).
23. “新冠肺炎”疫情期间某工厂为支持国家抗击疫情每天连夜生产急缺的消毒液,已知每瓶消毒液的生产成本为20元,为了合理定价,根据市场调查发现,当销售单价为30元时,每天的销售量为6000瓶,若销售单价每降低1元,则每天能多销售1000瓶,但要求销售单价不能低于成本且不高于30元.(1)、求每天的销售量 (瓶)与销售单价 (元)之间的函数关系式;(2)、求每天的利润 (元)与销售单价 (元)之间的函数关系式;(3)、该工厂负责人决定将每天的利润全部捐献出来进一步支持国家抗击“新冠肺炎”疫情,则当销售单价为多少元时,每天的销售利润最大?最大利润是多少?24. 如图1,在平面直角坐标系中,抛物线y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C(0,3),且抛物线的顶点坐标为(1,4).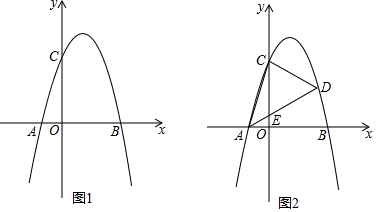 (1)、求抛物线的解析式;(2)、如图2,点D是第一象限抛物线上的一点,AD交y轴于点E,设点D的横坐标为m,设△CDE的面积为S,求S与m的函数关系式(不必写出自变量的取值范围);(3)、在(2)的条件下,连接AC,是否存在这样的点D,使得∠DAB=2∠ACO,若存在,求点D的坐标及相应的S的值,若不存在,请说明理由.
(1)、求抛物线的解析式;(2)、如图2,点D是第一象限抛物线上的一点,AD交y轴于点E,设点D的横坐标为m,设△CDE的面积为S,求S与m的函数关系式(不必写出自变量的取值范围);(3)、在(2)的条件下,连接AC,是否存在这样的点D,使得∠DAB=2∠ACO,若存在,求点D的坐标及相应的S的值,若不存在,请说明理由.