浙江省2020-2021年九年级上学期数学期末测试模拟卷B卷
试卷更新日期:2020-12-21 类型:期末考试
一、单选题
-
1. 已知 ,那么x的值是( )A、 B、 C、 D、2. 在一个不透明的袋中装着3个红球和1个黄球,它们只有颜色上的区别,随机从袋中摸出1个球,恰好是红球的概率为( )A、 B、 C、 D、3. 如图,已知C、D在以AB为直径的⊙O上,若∠CAB=30°,则∠D的度数是( )
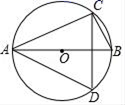 A、30° B、70° C、75° D、60°4. 下列事件中是随机事件的是( )A、通常加热到100℃时,水沸腾 B、在只装有黑球和白球的袋子里,摸出红球 C、购买一张彩票,中奖 D、太阳从东方升起5. 已知 ,则 ( )A、2 B、 C、3 D、6. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.某女老师上身长约61.8cm,下身长约96cm,为尽可能达到黄金比的美感效果好,她应穿的高跟鞋的高度大约为(精确到1cm)( )A、4cm B、5cm C、6cm D、7cm7. 下列各组线段中,长度成比例的是( )A、2cm、3cm、4cm、1cm B、1.5cm、2.5cm、4.5cm、6.5cm C、1.1cm、2.2cm、3.3cm、4.4cm D、1cm、2cm、2cm、4cm8. 如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( )
A、30° B、70° C、75° D、60°4. 下列事件中是随机事件的是( )A、通常加热到100℃时,水沸腾 B、在只装有黑球和白球的袋子里,摸出红球 C、购买一张彩票,中奖 D、太阳从东方升起5. 已知 ,则 ( )A、2 B、 C、3 D、6. 古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是 ( ≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.某女老师上身长约61.8cm,下身长约96cm,为尽可能达到黄金比的美感效果好,她应穿的高跟鞋的高度大约为(精确到1cm)( )A、4cm B、5cm C、6cm D、7cm7. 下列各组线段中,长度成比例的是( )A、2cm、3cm、4cm、1cm B、1.5cm、2.5cm、4.5cm、6.5cm C、1.1cm、2.2cm、3.3cm、4.4cm D、1cm、2cm、2cm、4cm8. 如图,⊙O的周长等于4πcm,则它的内接正六边形ABCDEF的面积是( )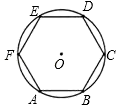 A、 B、 C、 D、9. 从地面竖直向上抛出一小球,小球的高度 h (单位: m )与小球运动时间 (单位: s )之间的函数关系如图所示.下列结论:
A、 B、 C、 D、9. 从地面竖直向上抛出一小球,小球的高度 h (单位: m )与小球运动时间 (单位: s )之间的函数关系如图所示.下列结论:①小球在空中经过的路程是 40m ;②小球运动的时间为 6s ;③小球抛出3秒时,速度为0;
④当 时,小球的高度 .其中正确的是( )
 A、①④ B、①② C、②③④ D、②④10. 如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3),若抛物线y=ax2的图象与正方形有公共点,则实数a的取值范围是( )
A、①④ B、①② C、②③④ D、②④10. 如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3),若抛物线y=ax2的图象与正方形有公共点,则实数a的取值范围是( )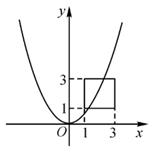 A、 ≤a≤3 B、 ≤a≤1 C、 ≤a≤3 D、 ≤a≤1
A、 ≤a≤3 B、 ≤a≤1 C、 ≤a≤3 D、 ≤a≤1二、填空题
-
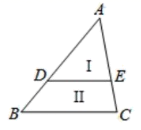
11. 函数y=x2﹣x﹣6的图象与x轴的交点坐标是12. 一个斜坡长 米,高 米,把重物从坡底沿着斜坡推进 米后停下,此时物体的高度是米13. 已知一个扇形的弧长为 ,圆心角是150°,则它的半径长为 , 扇形的面积为.14. 如图,已知DE∥BC且AD:DB=2:1,则SⅠ:SⅡ=
 15. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2),若点A′(5,6),则A的坐标为.
15. 如图,在平面直角坐标系中,△ABC和△A′B′C′是以坐标原点O为位似中心的位似图形,且点B(3,1),B′(6,2),若点A′(5,6),则A的坐标为.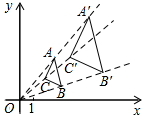 16. 如图,在平面直角坐标系中,已知点A(-1.5,0),B(0,2),将△ABO顺着x轴的正半轴无滑动的滚动,第一次滚动到①的位置,点B的对应点记作B1;第二次滚动到②的位置,点B1的对应点记作B2;第三次滚动到③的位置,点B2的对应点记作B3; ;依次进行下去,则点B2020的坐标为.
16. 如图,在平面直角坐标系中,已知点A(-1.5,0),B(0,2),将△ABO顺着x轴的正半轴无滑动的滚动,第一次滚动到①的位置,点B的对应点记作B1;第二次滚动到②的位置,点B1的对应点记作B2;第三次滚动到③的位置,点B2的对应点记作B3; ;依次进行下去,则点B2020的坐标为.
三、综合题
-
17. 已知 ,求 的值。18. 把二次函数y=﹣2x2﹣4x+5化成y=a(x-h)2+k形式,并求出它的图象顶点坐标、对称轴19. 复工复学后,为防控冠状病毒,学生进校园必须戴口罩,测体温。某校开通了两种不同类型的测温通道共三条,分别为:红外热成像测温(A通道)和人工测温(B通道和C通道),在三条通道中,每位同学都可随机选择其中的一条通过,周五有甲、乙两位同学进校园。(1)、当甲同学进校园时,从人工测温通道通过的概率是。(2)、请用列表或画树状图的方法求甲、乙两位同学从不同类型测温通道通过的概率。20. 如图,DE∥BC,EF∥CG,AD:AB=1:3,AE=3.
 (1)、求EC的值;(2)、求证:AD•AG=AF•AB.21. 如图,△ABC是正方形网格图中的格点三角形(顶点在格点上),请分别在图1和图2的正方形网格内按下列要求画出格点三角形.
(1)、求EC的值;(2)、求证:AD•AG=AF•AB.21. 如图,△ABC是正方形网格图中的格点三角形(顶点在格点上),请分别在图1和图2的正方形网格内按下列要求画出格点三角形. (1)、在图1中,画△DEF与△ABC相似,且相似比为 ;(2)、在图2中,画△PQR与△ABC相似,且相似比为 .22. 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.
(1)、在图1中,画△DEF与△ABC相似,且相似比为 ;(2)、在图2中,画△PQR与△ABC相似,且相似比为 .22. 如图,AB是⊙O的一条弦,OD⊥AB,垂足为C,交⊙O于点D,点E在⊙O上.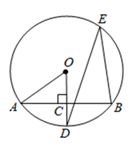 (1)、若∠AOD=52°,求∠DEB的度数;(2)、若AB=24,CD=8,求⊙O的半径长.23. 某商场要经营一种新上市的文具,进价为20元/件,试营业阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.(1)、写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)、商场的营销部结合实际情况,决定该文具的销售单价不低于30元,且每天的销售量不得少于160件,那么该文具如何定价每天的最大销售利润最大,最大利润是多少.24. 如图,在平面直角坐标系中,抛物线y=-x2+4x+m(m为常数)与y轴的交点为A,M(4,0)与N(0,-3) 分别是x轴、y轴上的点。
(1)、若∠AOD=52°,求∠DEB的度数;(2)、若AB=24,CD=8,求⊙O的半径长.23. 某商场要经营一种新上市的文具,进价为20元/件,试营业阶段发现:当销售单价是25元时,每天的销售量为250件;销售单价每上涨1元,每天的销售量就减少10件.(1)、写出商场销售这种文具,每天所得的销售利润w(元)与销售单价x(元)之间的函数关系式;(2)、商场的营销部结合实际情况,决定该文具的销售单价不低于30元,且每天的销售量不得少于160件,那么该文具如何定价每天的最大销售利润最大,最大利润是多少.24. 如图,在平面直角坐标系中,抛物线y=-x2+4x+m(m为常数)与y轴的交点为A,M(4,0)与N(0,-3) 分别是x轴、y轴上的点。 (1)、若抛物线过点M(4,0),求该抛物线顶点Q的坐标。(2)、若3≤x≤m时,抛物线y=-x2+4x+m有最小值-6,求m的值。(3)、连结AM,当AM的垂直平分线I恰好经过点N时,求直线I的解析式。(4)、若抛物线与线段MN有公共点,直接写出m的取值范围是。
(1)、若抛物线过点M(4,0),求该抛物线顶点Q的坐标。(2)、若3≤x≤m时,抛物线y=-x2+4x+m有最小值-6,求m的值。(3)、连结AM,当AM的垂直平分线I恰好经过点N时,求直线I的解析式。(4)、若抛物线与线段MN有公共点,直接写出m的取值范围是。