初中数学浙教版九年级上学期期末复习专题10 相似多边形、图形的位似

试卷更新日期：2020-12-20 类型：复习试卷

进入出卷网下载

一、单选题

1. 在平面直角坐标系中，已知点E（﹣4，2），F（﹣2，﹣2），以原点O为位似中心，相似比为0.5，把△EFO缩小，则点E的对应点E′的坐标是（）

A、（﹣2，1） B、（﹣8，4） C、（﹣2，1）或（2，﹣1） D、（﹣8，4）或（8，﹣4）

查看试题解析
2. 用放大镜观察一个五边形时，不变的量是（）

A、各边的长度 B、各内角的度数 C、五边形的周长 D、五边形的面积

查看试题解析
3. 如图，把一个矩形分割成四个全等的小矩形，要使小矩形与原矩形相似，则原矩形的长与宽之比为（）

A、2：1 B、4：1 C、 $\sqrt{2} ： 1$ D、1：2

查看试题解析
4. 如图， $△ A B C$ 与 $△ D E F$ 是位似图形，位似中心为 $O$ ， $O A ： A D = 3 ： 4$ ， $S_{△ A B C} = 9$ ，则 $△ D E F$ 的面积为（）

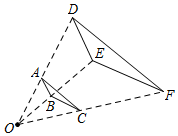A、12 B、16 C、21 D、49

查看试题解析
5. 将铁丝围成的△ABC铁框平行地面（水平）放置，并在灯泡的垂直照射下，在地面上的影子是△A′B′C′，那么△ABC与△A′B′C′之间是属于（）

A、对称变换 B、平移变换 C、位似变换 D、旋转变换

查看试题解析
6. 一个五边形的边长分别为2，3，4，5，6，另一个和它相似的五边形的最长边长为24，则这个五边形的最短边长为（）

A、6 B、8 C、12 D、10

查看试题解析
7. 如图， $Δ A B C$ 与 $Δ A^{'} B^{'} C^{'}$ 是位似图形，点 $O$ 是位似中心，若 $O A = 2 A A^{'}$ ， $S_{Δ A B C} = 4$ ，则 $S_{Δ A^{'} B^{'} C^{'}}$ 等于（）

A、6 B、8 C、9 D、12

查看试题解析
8. 如图，以点O为位似中心，把 $△ A B C$ 放大为原图形的2倍得到 $△ A^{'} B^{'} C^{'}$ ，以下说法中错误的是（）

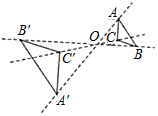A、 $△ A B C ∽ △ A^{'} B^{'} C^{'}$ · B、点C、点O、点 $C^{'}$ 三点在同一直线上 C、 $A O ： A A^{'} = 1 ： 2$ D、 $A B ∥ A^{'} B^{'}$

查看试题解析
9. 如图，在直角坐标系中，矩形OABC的顶点O在坐标原点，边OA在x轴上，OC在y轴上，如果矩形OA'B'C'与矩形OABC关于点O位似，且矩形OA'B'C'的面积等于矩形OABC面积的 $\frac{1}{4}$ ，那么点B'的坐标是（　　）

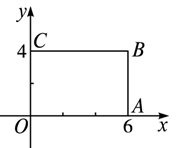A、（3，2） B、（－2，－3） C、（2，3）或（－2，－3） D、（3，2）或（－3，－2）

查看试题解析
10.
如图所示，一般书本的纸张是在原纸张多次对开得到．矩形ABCD沿EF对开后，再把矩形EFCD沿MN对开，依此类推．若各种开本的矩形都相似，那么 $\frac{A B}{A D}$ 等于（　　）.

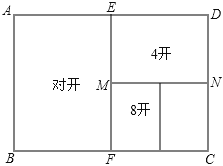A、0.618 B、 $\frac{\sqrt{2}}{2}$ C、 $\sqrt{2}$ D、2

查看试题解析

二、填空题

11. 若两个相似六边形的周长比是3∶2，其中较大六边形的面积为81，则较小六边形的面积为.

查看试题解析
12. 如图，若将平面直角坐标系中“鱼”以原点O为位似中心，按照相似比 $\frac{1}{2}$ 缩小，则点A的对应点的坐标是．

查看试题解析
13. 如图，矩形纸片 $A B C D$ 中， $A B > A D$ ， $E ， F$ 分别是 $A B ， D C$ 的中点，将矩形 $A B C D$ 沿 $E F$ 所在直线对折，若得到的两个小矩形都和矩形 $A B C D$ 相似，则用等式表示 $A B$ 与 $A D$ 的数量关系为．

查看试题解析
14.
如图，已知矩形OABC与矩形ODEF是位似图形，P是位似中心，若点B的坐标为（2，4），点E的坐标为（﹣1，2），则点P的坐标为

查看试题解析
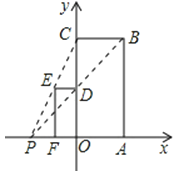15. 如图，四边形ABCD与四边形EFGH位似，其位似中心为点O ，且 $\frac{O E}{E A} = \frac{4}{3}$ ，则 $\frac{F G}{B C} =$ ．

查看试题解析
16. 如图，正六边形A₁B₁C₁D₁E₁F₁的边长为1，它的6条对角线围成一个正六边形A₂B₂C₂D₂E₂F₂；正六边形A₂B₂C₂D₂E₂F₂的6条对角线又围成一个正六边形A₃B₃C₃D₃E₃F₃…；如此继续下去，则六边形A₄B₄C₄D₄E₄F₄的面积是.

查看试题解析

三、综合题

17. 如图，四边形 $A B C D ∽$ 四边形 $A' B' C' D'$ .

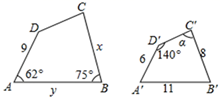(1)、 $α$ ＝，它们的相似比是.

(2)、求边x、y的长度.

查看试题解析
18. 如图， $△$ OAB与 $△$ ODC是位似图形。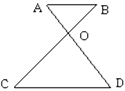
试问：

(1)、AB与CD平行吗？请说明理由。

(2)、如果OB=3，OC=4，OD=3.5.试求 $△$ OAB与 $△$ ODC的相似比及OA的长。

查看试题解析
19.
如图，△ABC中，AD、BE是高．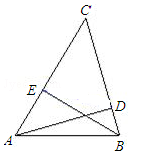

(1)、求证： $\frac{C D}{C E} = \frac{A C}{B C}$ ；

(2)、连接DE，那么△CDE与△CAB是位似图形吗？

查看试题解析
20.
数学课上，老师要求同学们在扇形纸片OAB上画出一个正方形，使得正方形的四个顶点分别落在扇形半径OA、OB和弧AB上．有一部分同学是这样画的：如图1，先在扇形OAB内画出正方形CDEF，使得C、D在OA上，F在OB上，连结OE并延长交弧AB与G点，过点G，作GJ⊥OA于点J，作GH⊥GJ交OB于点H，再作HI⊥OA于点I．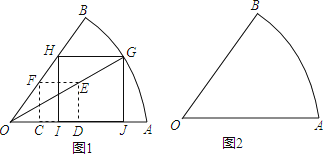
（1）请问他们画出的四边形GHIJ是正方形吗？如果是，请给出你的证明；如果不是，请说明理由；
（2）还有一部分同学用另外一种不同于图1的方法画出的，请你参照图1的画法，在图2上画出这个正方形（保留画图痕迹，不要求证明）．

查看试题解析
21. 如图，已知O是坐标原点，B、C两点的坐标分别为（3，﹣1）、（2，1）．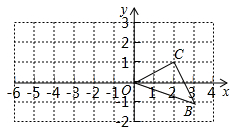

(1)、以0点为位似中心在y轴的左侧将△OBC放大到两倍（即新图与原图的相似比为2），画出图形；

(2)、分别写出B、C两点的对应点B′、C′的坐标；

(3)、如果△OBC内部一点M的坐标为（x，y），写出M的对应点M′的坐标．

查看试题解析