初中数学浙教版九年级上学期期末复习专题9 相似三角形
试卷更新日期:2020-12-20 类型:复习试卷
一、单选题
-
1. 如图, DE∥BC ,若 ,则△ADE与四边形BCED的面积的比是( )
 A、1:9 B、1:8 C、1:6 D、1:32. 通过一个3倍的放大镜看一个△ABC , 下面说法正确的是( )A、△ABC放大后,∠A是原来的3倍 B、△ABC放大后周长是原来的3倍 C、△ABC放大后,面积是原来的3倍 D、以上都不对3. 如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )
A、1:9 B、1:8 C、1:6 D、1:32. 通过一个3倍的放大镜看一个△ABC , 下面说法正确的是( )A、△ABC放大后,∠A是原来的3倍 B、△ABC放大后周长是原来的3倍 C、△ABC放大后,面积是原来的3倍 D、以上都不对3. 如图,△ABC中,∠A=65°,AB=6,AC=3,将△ABC沿图中的虚线剪开,剪下的阴影三角形与原三角形不构成相似的是( )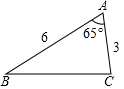 A、
A、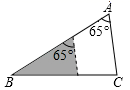 B、
B、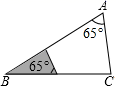 C、
C、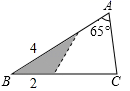 D、
D、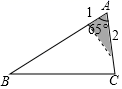 4. 若△ABC∽△DEF,且对应高线比为4:9,则△ABC与△DEF的周长比为( )A、2:3 B、3:2 C、4:9 D、16:815. 下列说法中错误的是( )A、如果两个三角形全等,那么这两个三角形相似 B、如果两个三角形相似,且相似比为1,那么这两个三角形必全等 C、如果两个三角形都与另一个三角形相似,那么这两个三角形相似 D、如果两个三角形相似,那么它们一定能互相重合6. 如图,已知在 中,D为 上一点, ,分别交 , , 于点E,F,G,则下列比例式正确的是( )
4. 若△ABC∽△DEF,且对应高线比为4:9,则△ABC与△DEF的周长比为( )A、2:3 B、3:2 C、4:9 D、16:815. 下列说法中错误的是( )A、如果两个三角形全等,那么这两个三角形相似 B、如果两个三角形相似,且相似比为1,那么这两个三角形必全等 C、如果两个三角形都与另一个三角形相似,那么这两个三角形相似 D、如果两个三角形相似,那么它们一定能互相重合6. 如图,已知在 中,D为 上一点, ,分别交 , , 于点E,F,G,则下列比例式正确的是( ) A、 B、 C、 D、7. 如图,身高为1.6 m的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2 m,BC=8 m,则旗杆的高度是( )
A、 B、 C、 D、7. 如图,身高为1.6 m的某学生想测量学校旗杆的高度,当他站在C处时,他头顶端的影子正好与旗杆顶端的影子重合,并测得AC=2 m,BC=8 m,则旗杆的高度是( ) A、6.4m B、7m C、8m D、9m8. 如图,在 , ,点D是边BC上的一点,且 , ,则a等于( )
A、6.4m B、7m C、8m D、9m8. 如图,在 , ,点D是边BC上的一点,且 , ,则a等于( ) A、 B、 C、1 D、29. 如图,锐角三角形 ,边 ,高 ,其内接的正方形的一边在 上,其余两个顶点分别在 , 上,则正方形的边长 为( )
A、 B、 C、1 D、29. 如图,锐角三角形 ,边 ,高 ,其内接的正方形的一边在 上,其余两个顶点分别在 , 上,则正方形的边长 为( )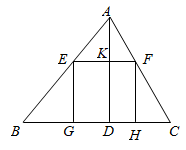 A、2.6 B、2.4 C、3 D、1.210. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A、2.6 B、2.4 C、3 D、1.210. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )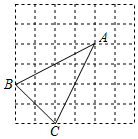 A、4个 B、5个 C、6个 D、7个
A、4个 B、5个 C、6个 D、7个二、填空题
-
11. 如图在Rt△ABC中,CD是斜边AB上的高,若AC= ,DB=4,则AD的长为.
 12. 的边长分别为 的边长分别 ,则 与 (选填“一定”“不一定” “一定不”)相似13. 如图,四边形 是三个正方形、
12. 的边长分别为 的边长分别 ,则 与 (选填“一定”“不一定” “一定不”)相似13. 如图,四边形 是三个正方形、 14. 如图,∠1=∠2,请补充一个条件: , 使 .
14. 如图,∠1=∠2,请补充一个条件: , 使 . 15. 如图,测量小玻璃管口径的量具ABC上,AB的长为10mm,AC被分为60等份,如果小管口DE正好对着量具上30份处(DE//AB),那么小管口径DE的长是mm.
15. 如图,测量小玻璃管口径的量具ABC上,AB的长为10mm,AC被分为60等份,如果小管口DE正好对着量具上30份处(DE//AB),那么小管口径DE的长是mm. 16. 如图,在 中, , 于点 , 于点 .交 于点 ,点 在直线 上运动, , , ,则 的最小值是 .
16. 如图,在 中, , 于点 , 于点 .交 于点 ,点 在直线 上运动, , , ,则 的最小值是 .
三、综合题
-
17. 为了估计河的宽度,勘测人员在河的对岸选定一个目标点A , 在近岸分别取点B、D、E、C , 使点A、B、D在一条直线上,且AD⊥DE , 点A、C、E也在一条直线上,且DE∥BC . 经测量BC=25米,BD=12米,DE=40米,求河的宽度AB为多少米?
 18. 如图,已知点D是 的边AC上的一点,连接 , , .
18. 如图,已知点D是 的边AC上的一点,连接 , , .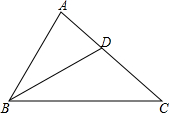 (1)、求证: ∽ ;(2)、求线段CD的长.19. 如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G.
(1)、求证: ∽ ;(2)、求线段CD的长.19. 如图,四边形ABCD中,AD∥BC,点E是边AD的中点,连接BE并延长交CD的延长线于点F,交AC于点G. (1)、若FD=2, ,求线段DC的长;(2)、求证:EF·GB=BF·GE.20. 在 中, 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连结EQ.设动点运动时间为x秒.
(1)、若FD=2, ,求线段DC的长;(2)、求证:EF·GB=BF·GE.20. 在 中, 现有两个动点P、Q分别从点A和点B同时出发,其中点P以1cm/s的速度,沿AC向终点C移动;点Q以1.25cm/s的速度沿BC向终点C移动.过点P作PE∥BC交AD于点E,连结EQ.设动点运动时间为x秒. (1)、用含x的代数式表示AE、DE的长度;(2)、当点Q在BD(不包括点B、D)上移动时,设 的面积为 ,求 与月份 的函数关系式,并写出自变量 的取值范围;(3)、当 为何值时, 为直角三角形.
(1)、用含x的代数式表示AE、DE的长度;(2)、当点Q在BD(不包括点B、D)上移动时,设 的面积为 ,求 与月份 的函数关系式,并写出自变量 的取值范围;(3)、当 为何值时, 为直角三角形.