初中数学浙教版九年级上学期期末复习专题8 比例线段
试卷更新日期:2020-12-20 类型:复习试卷
一、单选题
-
1. 若 ,则 的值等于( )A、 B、 C、 D、52. 已知线段b是线段a、c的比例中项,a=3,c=2,那么b的长度等于( )A、± B、6 C、 D、3. 已知三条线段的长分别为1.5,2,3,则下列线段中,不能与它们组成比例线段的是( )A、1 B、2.25 C、4 D、24. 如图,在 中, ,且 ,则 的值为( )
 A、1 B、2 C、 D、5. 如图,电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点大约( )m处是比较得体的位置.
A、1 B、2 C、 D、5. 如图,电视节目主持人在主持节目时,站在舞台的黄金分割点处最自然得体,若舞台AB长为20m,试计算主持人应走到离A点大约( )m处是比较得体的位置. A、12.36m B、7.64m C、12.36m或7.64m D、13.36m6. 若点C是线段AB的黄金分割点,且AB=2(AC>BC),则AC等于( )A、 ﹣1 B、3﹣ C、 D、 ﹣1或3﹣7. 如图,直线 ,若 , , ,则 的长为( )
A、12.36m B、7.64m C、12.36m或7.64m D、13.36m6. 若点C是线段AB的黄金分割点,且AB=2(AC>BC),则AC等于( )A、 ﹣1 B、3﹣ C、 D、 ﹣1或3﹣7. 如图,直线 ,若 , , ,则 的长为( )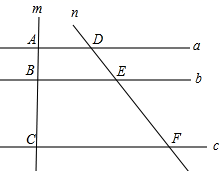 A、 B、 C、 D、8. 如图, ,在下列比例式中,不能成立的是( ).
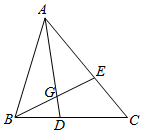
A、 B、 C、 D、8. 如图, ,在下列比例式中,不能成立的是( ).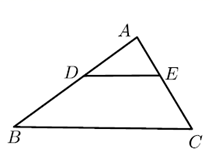 A、 B、 C、 D、9. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( ).
A、 B、 C、 D、9. 如图,在△ABC中,点D在BC边上,连接AD,点G在线段AD上,GE∥BD,且交AB于点E,GF∥AC,且交CD于点F,则下列结论一定正确的是( ). A、 B、 C、 D、10. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )
A、 B、 C、 D、10. 在欧几里得的《几何原本》中给出一个找线段的黄金分割点的方法.如图所示,以线段AB为边作正方形ABCD,取AD的中点E,连结BE,延长DA至F,使得EF=BE,以AF为边作正方形AFGH,则点H即是线段AB的黄金分割点.若记正方形AFGH的面积为S1 , 矩形BCIH的面积为S2 , 则S1 与S2的大小关系是( )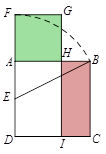 A、
A、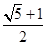 B、
B、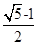 C、
D、1
C、
D、1
二、填空题
-
11. 在比例尺为1:40000的地图上,若某条道路长为5cm,则它的实际距离为km.12. 如图所示,乐器上的一根弦 ,两个端点 固定在乐器面板上,支撑点 是靠近点 的黄金分割点(即 是 与 的比例中项),支撑点 是靠近点 的黄金分割点,则 cm, cm.
 13. 已知点P是线段AB上的一点,且 ,如果AB=10cm , 那么BP=cm14. 如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为。
13. 已知点P是线段AB上的一点,且 ,如果AB=10cm , 那么BP=cm14. 如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为。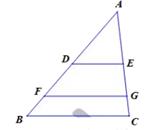 15.
15.已知实数a , b , c满足a+b+c=10,且 ,则 的值是
三、综合题
-
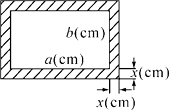
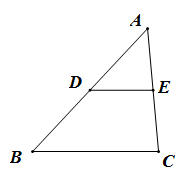
16. 在一张比例尺为 的地图上,有一块多边形区域的周长是 ,面积是 ,求这个区域的实际周长和面积.17. 在△ABC中,AB=12,点E在AC上,点D在AB上,若AE=6,EC=4, 。(1)、求AD的长;(2)、试问 能成立吗?请说明理由。