初中数学浙教版九年级上学期期末复习专题7 正多边形、弧长及扇形的面积
试卷更新日期:2020-12-20 类型:复习试卷
一、单选题
-
1. 如图,AB为⊙O的直径,AB=30,点C在⊙O上,∠A=24°,则 的长为( )
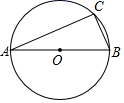 A、9π B、10π C、11π D、12π2. 如图,一个圆形飞镖板被分为四个圆心角相等的扇形,若大圆半径为2,小圆半径为1,则阴影部分的面积为( )
A、9π B、10π C、11π D、12π2. 如图,一个圆形飞镖板被分为四个圆心角相等的扇形,若大圆半径为2,小圆半径为1,则阴影部分的面积为( )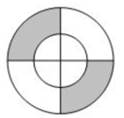 A、π B、 π C、3π D、 π3. 圆内接正六边形的边长与该边所对的劣弧的长的比是( )A、1: B、1:π C、3:π D、6:π4. 如图1,一只蚂蚁从点O出发,以1厘米/秒速度沿着扇形AOB的边缘爬行一周。设爬行时间为x秒,蚂蚁到点O的距离为y厘米,y关于x的函数图象如图2所示,则扇形的面积为( )
A、π B、 π C、3π D、 π3. 圆内接正六边形的边长与该边所对的劣弧的长的比是( )A、1: B、1:π C、3:π D、6:π4. 如图1,一只蚂蚁从点O出发,以1厘米/秒速度沿着扇形AOB的边缘爬行一周。设爬行时间为x秒,蚂蚁到点O的距离为y厘米,y关于x的函数图象如图2所示,则扇形的面积为( )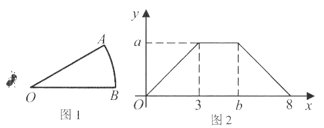 A、3 B、6 C、 π D、π5. 如图,扇形纸扇完全打开后,外侧两竹条AB,AC夹角为150°,AB的长为32cm,BD的长为14cm,则 的长为( )cm.
A、3 B、6 C、 π D、π5. 如图,扇形纸扇完全打开后,外侧两竹条AB,AC夹角为150°,AB的长为32cm,BD的长为14cm,则 的长为( )cm. A、 π B、12π C、15π D、36π6. 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的 ,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )
A、 π B、12π C、15π D、36π6. 如图,将等边△ABC的边AC逐渐变成以B为圆心、BA为半径的 ,长度不变,AB、BC的长度也不变,则∠ABC的度数大小由60°变为( )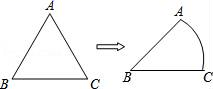 A、( )° B、( )° C、( )° D、( )°7. 如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )
A、( )° B、( )° C、( )° D、( )°7. 如图,从一块直径为 的圆形铁皮上剪出一个圆心角为90°的扇形.则此扇形的面积为( )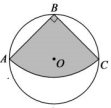 A、 B、 C、 D、8. 如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )
A、 B、 C、 D、8. 如图,AB为半圆的直径,且AB=4,半圆绕点B顺时针旋转45°,点A旋转到A′的位置,则图中阴影部分的面积为( )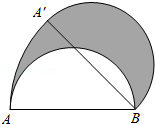 A、 B、π C、2π D、4π9. 如图,在圆内接正六边形ABCDEF中,BF,BD分别交AC于点G,H.若该圆的半径为15cm,则线段GH的长为( )
A、 B、π C、2π D、4π9. 如图,在圆内接正六边形ABCDEF中,BF,BD分别交AC于点G,H.若该圆的半径为15cm,则线段GH的长为( )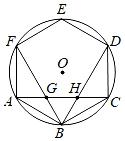 A、 cm B、5 cm C、3 cm D、10 cm10.
A、 cm B、5 cm C、3 cm D、10 cm10.如图,一个小圆沿着一个五边形的边滚动,如果五边形的各边长都和小圆的周长相等,那么当小圆滚动到原来位置时,小圆自身滚动的圈数是( )
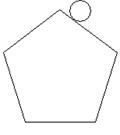 A、4 B、5 C、6 D、10
A、4 B、5 C、6 D、10二、填空题
-
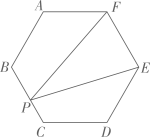
11. 一个扇形的面积为 ,半径为6cm,则扇形的圆心角是度.12. 如图,在边长为 的正六边形 中,点P在BC上,则 的面积为.
 13. 如图,边AB是⊙O内接正六边形的一边,点C在 上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n=.
13. 如图,边AB是⊙O内接正六边形的一边,点C在 上,且BC是⊙O内接正八边形的一边,若AC是⊙O内接正n边形的一边,则n=.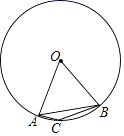 14. 如图,在圆心角为120°的扇形OAB中,半径OA=2,C为 的中点,D为OA上任意一点(不与点O、A重合),则图中阴影部分的面积为.
14. 如图,在圆心角为120°的扇形OAB中,半径OA=2,C为 的中点,D为OA上任意一点(不与点O、A重合),则图中阴影部分的面积为.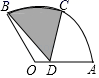 15. 如图,在扇形 中, 平分 交狐 于点D.点E为半径 上一动点若 ,则阴影部分周长的最小值为.
15. 如图,在扇形 中, 平分 交狐 于点D.点E为半径 上一动点若 ,则阴影部分周长的最小值为.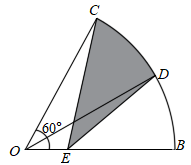 16. 如图,在正方形ABCD的边长为3,以A为圆心,2为半径作圆弧.以D为圆心,3为半径作圆弧.若图中阴影部分的面积分为 、 .则 =。
16. 如图,在正方形ABCD的边长为3,以A为圆心,2为半径作圆弧.以D为圆心,3为半径作圆弧.若图中阴影部分的面积分为 、 .则 =。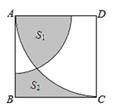
三、综合题
-
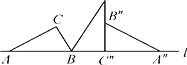
17. 如图,把Rt△ABC的斜边放在直线l上,按顺时针方向在l上转动两次,使它转到△A″B″C″位置.设BC=1,AC= ,求当顶点A运动到A″位置时,点A经过的路线长度.
 18. 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,以O为圆心,OA为半径作⊙O,与BC相切于点D,且交AB于点E。
18. 如图,在Rt△ABC中,∠C=90°,AC=BC,点O在AB上,以O为圆心,OA为半径作⊙O,与BC相切于点D,且交AB于点E。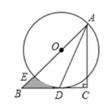 (1)、连结AD,求证:AD平分∠CAB;(2)、若BE= -1,求阴影部分的面积。
(1)、连结AD,求证:AD平分∠CAB;(2)、若BE= -1,求阴影部分的面积。