初中数学浙教版九年级上学期期末复习专题5 圆、图形的旋转及垂径定理
试卷更新日期：2020-12-20 类型：复习试卷
一、单选题
-
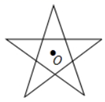
1. 已知⊙O的半径为1cm，点D到圆心O的距离为2cm,则点D与⊙O的位置关系是（ ）A、点D在⊙O外 B、点D在⊙O上 C、点D在⊙O内 D、不能确定2. 如图，是国旗中的一颗五角星图案，绕着它的中心旋转，要使旋转后的五角星能与自身重合，则旋转角的度数至少为（ ）.
A、30° B、45° C、60° D、72°3. 下列说法：①直径是弦；②长度相等的两条弧是等弧；③半圆是弧，但弧不一定是半圆；④圆的对称轴是直径；⑤外心在三角形的一条边上的三角形是直角三角形，正确的命题有 （ ）A、1个 B、2个 C、3个 D、4个4. 如图，AB是⊙O的直径，C，D是⊙O上的两点，且BC平分∠ABD，AD分别与BC，OC相交于点E，F，则下列结论不一定成立的是（ ）
A、OC∥BD B、AD⊥OC C、△CEF≌△BED D、AF＝FD5. 如图所示， 中， ，将 绕点A顺时针方向旋转 ，对应得到 ，则 的度数为（ ）
A、 B、 C、 D、6. 如图，在5x5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是（ ）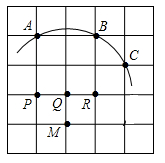
A、点P B、点Q C、点R D、点M7. 已知点A（-1， ），O为坐标原点，连接OA.将线段OA绕点O按逆时针方向旋转 得到线段 ，则点 的坐标为（ ）A、 ， B、 ， C、 ， D、 ，8. 如图，将△ABC绕点A逆时针旋转得到△ADE，其中点B、C分别与点D、E对应，如果B、D、C三点恰好在同一直线上，那么下列结论错误的是（ ）
A、∠ACB＝∠AED B、∠BAD＝∠CAE C、∠ADE＝∠ACE D、∠DAC＝∠CDE9. 如图，一段抛物线：y=﹣x（x﹣5）（0≤x≤5），记为C1 ， 它与x轴交于点O，A1；将C1绕点A1旋转180°得C2 ， 交x轴于点A2；将C2绕点A2旋转180°得C3 ， 交x轴于点A3；…如此进行下去，得到一“波浪线”，若点P（2018，m）在此“波浪线”上，则m的值为（ ）
A、4 B、﹣4 C、﹣6 D、610. 一个点到圆的最大距离为11cm，最小距离为5cm，则圆的半径为（ ）A、16cm或6cm， B、3cm或8cm C、3cm D、8cm二、填空题
-
11. 已知⊙O的半径为5cm，则圆中最长的弦长为cm.12. 中，两条直角边的长分别是6cm和8cm，则 的外接圆的半径是cm.13. 如图是一条水铺设的直径为2米的通水管道横截面，其水面宽1.6米，则这条管道中此时水深为米.
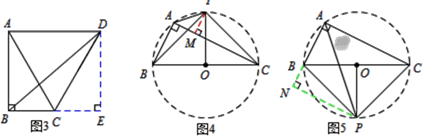
14. 如图，在⊙O中，AB＝2CD，那么 2 （填“＞，＜或＝”）
15. 如图，在△OAB 中，∠AOB＝90°，AO＝3，BO＝4.将△OAB 绕顶点 O 按顺时针方向旋转到△OA1B1 处，此时线段 OB1 与 AB 的交点 D 恰好为线段 AB 的中点， 线段 A1B1 与 OA 交于点 E，则图中阴影部分的面积.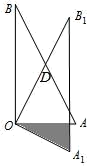
三、综合题
-
16. 如图，已知在以点O为圆心的两个同心圆中，大圆的弦AB交小圆于C，D．
(1)、求证：AC=BD；(2)、若大圆的半径R=10，小圆半径r=8，且圆心O到直线AB的距离为6，求AC的长
17. 一跨河桥，桥拱是圆弧形，跨度（AB）为16米，拱高（CD）为4米，求：
(1)、桥拱半径.(2)、若大雨过后，桥下河面宽度（EF）为12米，求水面涨高了多少？18. 在平面直角坐标系xOy中的点P和图形M，给出如下的定义：若在图形M上存在一点Q，使得P、Q两点间的距离小于或等于1，则称P为图形M的关联点．(1)、当⊙O的半径为2时，①在点P1（ ，0），P2（ ， ），P3（ ，0）中，⊙O的关联点是 ．
②点P在直线y＝﹣x上，若P为⊙O的关联点，求点P的横坐标的取值范围．
(2)、⊙C的圆心在x轴上，半径为2，直线y＝﹣x+1与x轴、y轴交于点A、B．若线段AB上的所有点都是⊙C的关联点，直接写出圆心C的横坐标的取值范围．19. 如图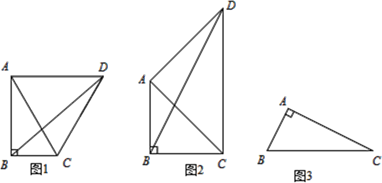
问题发现：
(1)、如图1，在Rt△ABC中，∠BAC=30°，∠ABC＝90°，将线段AC绕点A逆时针旋转，旋转角α=2∠BAC， ∠BCD的度数是；线段BD，AC之间的数量关系是.(2)、在Rt△ABC中，∠BAC=45°，∠ABC＝90°，将线段AC绕点A逆时针旋转，旋转角α=2∠BAC，请问（1）中的结论还成立吗？；(3)、如图3，在Rt△ABC中，AB＝2，AC＝4，∠BDC＝90°，若点P满足PB＝PC，∠BPC＝90°，请直接写出线段AP的长度.