初中数学浙教版九年级上学期期末复习专题1 二次函数的图象与性质
试卷更新日期:2020-12-20 类型:复习试卷
一、单选题
-
1. 下列函数中是二次函数的是( )A、 B、 C、 D、2. 抛物线 的顶点坐标( )A、(﹣3,4) B、(﹣3,﹣4) C、(3,﹣4) D、(3,4)3. 抛物线 经过平移得到抛物线 ,平移过程正确的是( )A、先向左平移6个单位,再向上平移3个单位 B、先向左平移6个单位,再向下平移3个单位 C、先向右平移6个单位,再向上平移3个单位 D、先向右平移6个单位,再向下平移3个单位4. 要在抛物线y=x(4-x)上找点P(a,b),针对b的不同取值,所找点P的个数,三人的说法如下( )
甲:若b=5,则点p的个数为0
乙:若b=4,则点P的个数为1
丙:若b=3,则点P的个数为1
A、甲乙错,丙对 B、甲丙对,乙错 C、甲乙对,丙错 D、乙丙对,甲错5. 已知二次函数y=﹣x2+2x+3的图象过点M(﹣2,y1),N(﹣3,y2),K(6,y3),则y1 , y2 , y3的关系从小到大的是( )A、y1<y2<y3 B、y3<y2<y1 C、y2<y1<y3 D、y3<y1<y26. 在平面直角坐标系中,抛物线y=(x+3)(x﹣1)经过变换后得到抛物线y=(x+1)(x﹣3),则这个变换可以是( )A、向左平移2个单位 B、向右平移2个单位 C、向左平移4个单位 D、向右平移4个单位7. 已知在二次函数y=-x2+(a-1)x+1,当x>1时,y随x的增大而减小,则a的取值范围是( )A、a=-1 B、a=3 C、a≥-1 D、a≤38. 已知抛物线y=ax2+bx+c(a≠0)如图所示,那么a、b、c的取值范围是( ) A、a<0、b>0、c>0 B、a<0、b<0、c>0 C、a<0、b>0、c<0 D、a<0、b<0、c<09. 抛物线y=ax2+bx+c的对称轴为直线x=﹣1,图象过(1,0)点,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b+c<0.其中正确的个数有( )
A、a<0、b>0、c>0 B、a<0、b<0、c>0 C、a<0、b>0、c<0 D、a<0、b<0、c<09. 抛物线y=ax2+bx+c的对称轴为直线x=﹣1,图象过(1,0)点,部分图象如图所示,下列判断中:①abc>0;②b2﹣4ac>0;③9a﹣3b+c=0;④若点(﹣0.5,y1),(﹣2,y2)均在抛物线上,则y1>y2;⑤5a﹣2b+c<0.其中正确的个数有( )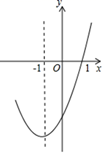 A、2 B、3 C、4 D、510. 如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3),若抛物线y=ax2的图象与正方形有公共点,则实数a的取值范围是( )
A、2 B、3 C、4 D、510. 如图,正方形四个顶点的坐标依次为(1,1),(3,1),(3,3),(1,3),若抛物线y=ax2的图象与正方形有公共点,则实数a的取值范围是( )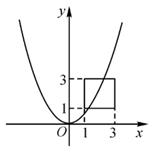 A、 ≤a≤3 B、 ≤a≤1 C、 ≤a≤3 D、 ≤a≤1
A、 ≤a≤3 B、 ≤a≤1 C、 ≤a≤3 D、 ≤a≤1二、填空题
-
11. 已知抛物线y=ax2-3x+a2-1经过坐标原点,且开口向下,则实数a的值为.12. 关于x的函数 是二次函数,则m= .13. 把抛物线 向下平移3个单位后得到抛物线 ,则 , .14. 若抛物线经过点A(2,7)和点B(-4,7),那么该抛物线的对称轴是直线 .15. 当x=x1和x= x2(x1≠x2)时,二次函数y=3x2﹣3x+4的函数值相等、当x=x1+x2时,函数值是.16. 如图,抛物线y=﹣x2+2x+m+1(m为常数)交y轴于点A,与x轴的一个交点在2和3之间,顶点为B.
①若点M(﹣2,y1)、点N( ,y2)、点P(2,y3)在该函数图象上,则y1<y2<y3;
②将该抛物线向左平移2个单位,再向下平移2个单位,所得抛物线解析式为y=﹣(x+1)2+m;
③抛物线y=﹣x2+2x+m+1与直线y=m+3有且只有一个交点;
④点A关于直线x=1的对称点为C,点D、E分别在x轴和y轴上,当m=1时,四边形BCDE周长的最小值为 .
其中正确判断的序号是.

三、综合题
-
17. 已知二次函数y=2x2+4x﹣6,(1)、将二次函数的解析式化为y=a(x﹣h)2+k的形式.(2)、写出二次函数图象的开口方向、对称轴、顶点坐标.18. 已知抛物线 经过点(1,0),(0, ).(1)、求该抛物线的函数表达式;(2)、抛物线 可以由抛物线 怎样平移得到?请写出一种平移的方法.19. 已知抛物线y=-x2+2x+2(1)、该抛物线的对称轴是直线 , 顶点坐标为;(2)、填写下表,并在如图的直角坐标系内描点画出该抛物线。
x
…
-1
1
3
…
y
…
2
2
-1
…
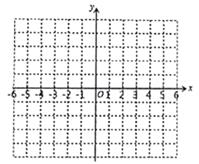 (3)、若A(x1 , y1),B(x2 , y1),C(I,y3)为抛物线y=-x2+2x+2上的三点,且x1<x2<1,则y1 , y2 , y3的大小关系是。20. 定义:将函数l的图象绕点 旋转 ,得到新的函数 的图象,我们称函数 是函数关于点P的相关函数. 例如:当 时,函数 关于点 的相关函数为 .(1)、当 , 时
(3)、若A(x1 , y1),B(x2 , y1),C(I,y3)为抛物线y=-x2+2x+2上的三点,且x1<x2<1,则y1 , y2 , y3的大小关系是。20. 定义:将函数l的图象绕点 旋转 ,得到新的函数 的图象,我们称函数 是函数关于点P的相关函数. 例如:当 时,函数 关于点 的相关函数为 .(1)、当 , 时①一次函数 关于点P的相关函数 ;
②点 在函数关于点P的相关函数的图象上,求a的值.
(2)、函数 关于点P的相关函数 ,则 ;(3)、当 时,函数 关于点 的相关函数的最大值为 ,求m的值.