广东省惠州市惠城区四校联考2020-2021学年九年级上学期数学12月月考试卷
试卷更新日期:2020-12-18 类型:月考试卷
一、选择题 (本题共计10小题,每题3分,共计30分)
-
1. 下列等式中,一定是一元二次方程的是( )A、 B、 C、 D、 ( , 为常数)2. 点 到 的圆心距离为 , 的半径为 ,点 与 的位置关系是( )A、点在圆外 B、点在圆上 C、点在圆内 D、无法确定3. 如图, 的直径为10,圆心 到弦 的距离 的长为3,则弦 的长是( )
 A、4 B、6 C、7 D、84. 如图,将 (其中 , ),绕 点按顺时针方向旋转到 的位置,使得点 , , 在同一直线上,则旋转角的度数为( )
A、4 B、6 C、7 D、84. 如图,将 (其中 , ),绕 点按顺时针方向旋转到 的位置,使得点 , , 在同一直线上,则旋转角的度数为( )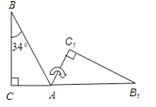 A、 B、 C、 D、5. 如图,四边形 是 的内接四边形,若 ,则 的度数为( )
A、 B、 C、 D、5. 如图,四边形 是 的内接四边形,若 ,则 的度数为( )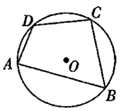 A、 B、 C、 D、6. 如图, , , 是半径为 的 上的三点,如果 ,那么 的长为( )
A、 B、 C、 D、6. 如图, , , 是半径为 的 上的三点,如果 ,那么 的长为( )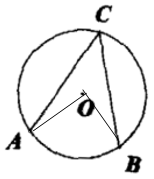 A、π B、 C、 D、7. 如图, 是 的直径, , 是 上两点.若 ,则 的度数为( )
A、π B、 C、 D、7. 如图, 是 的直径, , 是 上两点.若 ,则 的度数为( )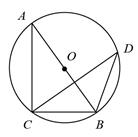 A、 B、 C、 D、8. 平面直角坐标系中,将抛物线 先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )A、 B、 C、 D、9. 在同一坐标系中,二次函数 与一次函数 的图象可能是( )A、
A、 B、 C、 D、8. 平面直角坐标系中,将抛物线 先向右平移1个单位,再向上平移2个单位,得到的抛物线的解析式是( )A、 B、 C、 D、9. 在同一坐标系中,二次函数 与一次函数 的图象可能是( )A、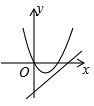 B、
B、 C、
C、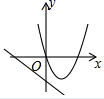 D、
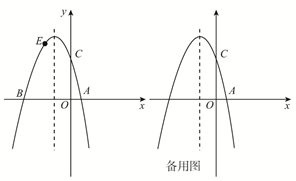
D、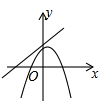 10. 如图,抛物线 的顶点为 ,与 轴的交点 在点 和 之间,下列结论正确的有( )
10. 如图,抛物线 的顶点为 ,与 轴的交点 在点 和 之间,下列结论正确的有( )① ;② ;③ ;④ .
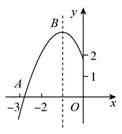 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题 (本题共计7小题,每题4分 ,共计28分 )
-
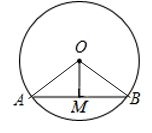
11. 点 关于原点对称的点的坐标是 .12. 如果抛物线 有最低点,那么 的取值范围是 .13. 圆锥的母线长为 ,底面圆半径为 ,则圆锥的侧面积为 (结果保留 ).14. 如图,在 中,点 是 的内心, , .
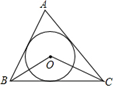 15. 如图,抛物线 = 与直线 = 相交于点 , ,则关于 的方程 = 的解为 .
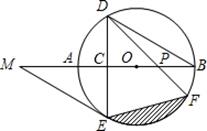
15. 如图,抛物线 = 与直线 = 相交于点 , ,则关于 的方程 = 的解为 . 16. 如图,抛物线 与 轴交于 、 两点, 是以点 为圆心, 为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是 .
16. 如图,抛物线 与 轴交于 、 两点, 是以点 为圆心, 为半径的圆上的动点, 是线段 的中点,连结 .则线段 的最大值是 .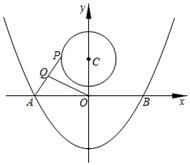 17. 如图,已知等腰 , ,以 为直径的圆交 于点 ,过点 的 的切线交 于点 ,若 , ,则 的半径是.
17. 如图,已知等腰 , ,以 为直径的圆交 于点 ,过点 的 的切线交 于点 ,若 , ,则 的半径是.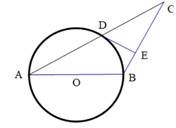
三、解答题 (本题共计8小题,共计62分)
-
18. 解方程: .19. 如图在边长为 的小正方形组成的网格中, 的顶点都在格点上.
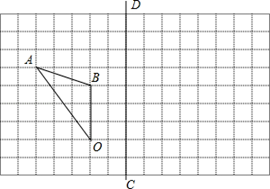
①请作出 关于直线 对称的 ;
②请将 绕点 顺时针旋转 ,画出旋转后的 .20. 抛物线 .(1)、请把二次函数写成 的形式;(2)、 取何值时, 随 的增大而减小?21. 如图, 的平分线交 的外接圆于点 , 的平分线交 于点 .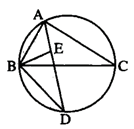 (1)、求证: ;(2)、若 , ,求 外接圆的半径.22. 某商店原来平均每天可销售某种水果200千克,每千克可盈利6元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可所多售出20千克.(1)、设每千克水果降价x元,平均每天盈利y元,试写出y关于x的函数表达式;(2)、若要平均每天盈利960元,则每千克应降价多少元?23. 已知关于 的一元二次方程 .(1)、求证:对于任意实数 ,方程都有实数根;(2)、当 为何值时,方程的一个根为 ?
(1)、求证: ;(2)、若 , ,求 外接圆的半径.22. 某商店原来平均每天可销售某种水果200千克,每千克可盈利6元,为减少库存,经市场调查,如果这种水果每千克降价1元,则每天可所多售出20千克.(1)、设每千克水果降价x元,平均每天盈利y元,试写出y关于x的函数表达式;(2)、若要平均每天盈利960元,则每千克应降价多少元?23. 已知关于 的一元二次方程 .(1)、求证:对于任意实数 ,方程都有实数根;(2)、当 为何值时,方程的一个根为 ?