初中数学苏科版八年级上学期期末复习专题（9）平面直角坐标系

试卷更新日期：2020-12-18 类型：复习试卷

进入出卷网下载

一、单选题

1. 已知点A（a﹣2，a+1）在x轴上，则a等于（　　）

A、1 B、0 C、﹣1 D、2

查看试题解析
2. 如果点A（m，﹣n）在第二象限，那么点B（﹣m，|n|）在（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
3. 已知点A（2- $a$ ， $a$ +1）在第四象限，则 $a$ 的取值范围是（）

A、 $a$ >2 B、-1< $a$ <2 C、 $a$ <-1 D、 $a$ <1

查看试题解析
4. 点A到x轴的距离是3，到y轴的距离是6，且点A在第二象限，则点A的坐标是（）

A、(-3，6) B、(-6，3) C、(3，-6) D、(8，-3)

查看试题解析
5. 以方程组 ${\begin{array}{l} x + y = 2 \\ y = x - 1 \end{array}$ 的解为坐标的点(x，y)在平面直角坐标系中的位置是（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
6. 下图是利用平面直角坐标系画出的北京世园会部分景区图．若这个坐标系分别以正东、正北方向为x轴、y轴的正方向，表示竹里馆的点的坐标为（-3，1），表示海坨天境的点的坐标为（-2，4），则下列表示国际馆的点的坐标正确的是（）

A、（8，1） B、（7，-2） C、（4，2） D、（-2，1）

查看试题解析
7. 在平面直角坐标系中，把△ABC的各顶点的横坐标都除以 $\frac{1}{4}$ ，纵坐标都乘 $\frac{1}{3}$ ，得到△DEF，把△DEF与△ABC相比，下列说法中正确的是（）

A、横向扩大为原来的4倍，纵向缩小为原来的 $\frac{1}{3}$ B、横向缩小为原来的 $\frac{1}{4}$ ，纵向扩大为原来的3倍 C、△DEF的面积为△ABC面积的12倍 D、△DEF的面积为△ABC面积的 $\frac{1}{12}$

查看试题解析
8. 如图，直角坐标系中，点 A（ − 2，2）、B（0，1）点 P 在 x 轴上，且△PAB 的等腰三角形，则满足条件的点 P 共有（）个

A、1 B、2 C、3 D、4

查看试题解析
9. 直角坐标系中，我们定义横、纵坐标均为整数的点为整点在0<x<3内，直线y=x+2和y=-x所围成的区域中，整点一共有（）

A、8个 B、7个 C、6个 D、5个

查看试题解析
10. 定义：平面内的直线l₁与l₂相交于点O ，对于该平面内任意一点M ，点M到直线l₁、l₂的距离分别为a、b ，则称有序非实数对（a ， b）是点M的“距离坐标”，根据上述定义，距离坐标为（2，1）的点的个数有（　　）.

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

11. 已知点P（2，﹣6），点P到x轴的距离为a ，到y轴的距离为b ，则a﹣b＝．

查看试题解析
12. 若点p(a+ $\frac{1}{3}$ ，2a+ $\frac{2}{3}$ )在第二，四象限角平分线上，则a=.

查看试题解析
13. 平面直角坐标系中，已知点A（2，-1），线段AB∥x轴，且AB=3，则点B的坐标为．

查看试题解析
14. 在直角坐标系中，坐标轴上到点P（﹣3，﹣4）的距离等于5的点共有个.

查看试题解析
15. 如图，长方形ABCO中，AB=2，BC=5，且如图放置在坐标系中，若将其沿着OB对折后，A'为点A的对应点，则OA'与BC的交点D的坐标为.

查看试题解析
16. 如图，∠ACB＝90°，AC＝BC，点C(1，2)、A(－2，0)，则点B的坐标是.

查看试题解析
17. 如图所示，直线y＝x+2与两坐标轴分别交于A、B两点，点C是OB的中点，D、E分别是直线AB、y轴上的动点，当△CDE周长最小时，点D的坐标为．

查看试题解析
18. 如图：将边长为1的正三角形OAP，沿x轴正方向连续翻转若干次，点A依次落在点A₁ ， A₂ ， A₃ ， A₄ ， …，A₂₀₁₉的位置上，则点A₂₀₁₉的坐标为.

查看试题解析

三、综合题

19. 已知点P（a﹣2，2a+8），分别根据下列条件求出点P的坐标.

(1)、点P在x轴上；

(2)、点Q的坐标为（1，5），直线PQ∥y轴；

(3)、点P到x轴、y轴的距离相等.

查看试题解析
20. 如图，在平面直角坐标系中， $Δ A B C$ 的三个顶点坐标分别为 $A (1 ， 1)$ ， $B (3 ， 4)$ ， $C (4 ， 2)$ ．

(1)、在图中画出 $Δ A B C$ 关于 $x$ 轴对称的 $Δ A_{1} B_{1} C_{1}$ ；

(2)、通过平移，使 $C_{1}$ 移动到原点 $O$ 的位置，画出平移后的 $Δ A_{2} B_{2} C_{2}$ ．

(3)、在 $Δ A B C$ 中有一点 $P (m ， n)$ ，则经过以上两次变换后点 $P$ 的对应点 $P_{2}$ 的坐标为．

查看试题解析
21. 如图，在平面直角坐标系中，四边形ABCD的顶点都在格点上，其中A点坐标为（﹣2，﹣1），C点坐标为（3，3）.

(1)、填空：点B到y轴的距离为，点B到直线AD的距离为；

(2)、求四边形ABCD的面积；

(3)、点M在y轴上，当△ADM的面积为12时，请直接写出点M的坐标.

查看试题解析
22. 如图，一只蚂蚁在网格（每小格边长为1）上沿着网格线运动．它从格点 $A (1 ， 2)$ 处出发去看望格点B、C、D等处的蚂蚁，规定：向上向右走均为正，向下向左走均为负．如：从A到B记为： $A \to B 〈 + 1 ， + 3 〉$ ，从B到A记为： $B \to A 〈 - 1 ， - 3 〉$ ，其中第一个数表示左右方向，第二个数表示上下方向．

(1)、填空：图中 $A \to C <____，____>$ ， $C \to____<____， \underline{^{} + 3^{}} >$ ；

(2)、若这只蚂蚁从A处去M处的蚂蚁的行走路线依次为 $〈 + 3 ， + 3 〉$ ， $〈 + 2 ， - 1 〉$ ， $〈 - 3 ， - 3 〉$ ， $〈 + 4 ， + 2 〉$ ，则点M的坐标为（，）；

(3)、若图中另有两个格点Р、Q ，且 $P \to A < m + 3 ， n + 2 >$ ， $P \to Q 〈 m + 1 ， n - 2 〉$ ，则从Q到A记为．

查看试题解析
23. 如图，已知在平面直角坐标系中，A（0，﹣1）、B（﹣2，0）C（4，0）

(1)、求△ABC的面积；

(2)、在y轴上是否存在一个点D，使得△ABD为等腰三角形，若存在，求出点D坐标；若不存，说明理由.

查看试题解析
24. 定义：①已知A(x₁ ， y₁)、B(x₂ ， y₂)，则AB= $\sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2}}$ ；② 已知A(x₀ ， y₀)直线 l 的方程为 Ax + By + C= 0，则 A 到直线的距离 $d = \frac{| A x_{0} + B y_{0} + C |}{\sqrt{A^{2} + B^{2}}}$

(1)、已知 A(2,5)、 B(-1,1)，求 AB ；

(2)、已知 A(2,1)，直线l : 3x+ 4y+ 5 = 0，求 A 到直线的距离；

(3)、求两平行直线3x+ 4y+1 = 0与3x+ 4 y+ 8 = 0之间的距离；

(4)、求 $\sqrt{x^{2} + 4 x + 5} + \sqrt{x^{2} - 6 x + 25}$ 的最小值.

查看试题解析
25. 如图①，我们在“格点”直角坐标系上可以看到：要找 $A B$ 或 $D E$ 的长度，可以转化为求 $R t Δ A B C$ 或 $R t Δ D E F$ 的斜边长.

例如：从坐标系中发现： $A (4 ， 5)$ ， $B (1 ， 1)$ ，所以 $A C = | 5 - 1 | = 4$ ， $B C = | 4 - 1 | = 3$ ，所以由勾股定理可得： $A B = \sqrt{4^{2} + 3^{2}} = \sqrt{25} = 5$ .

(1)、在图①中请用上面的方法求线段 $D E$ 的长： $D E =$ ；在图②中：设 $A (x_{1} ， y_{1})$ ， $B (x_{2} ， y_{2})$ ，试用 $x_{1}$ ， $x_{2}$ ， $y_{1}$ ， $y_{2}$ 表示： $A B =$ .

(2)、试用(1)中得出的结论解决如下题目：已知： $A (2 ， - 1)$ ， $B (4 ， 2)$ ， $C$ 为 $x$ 轴上的点，且使得 $Δ A B C$ 为等腰三角形，请求出 $C$ 点的坐标.

查看试题解析
26. 如图1，A（﹣2，0），B（0，4），以B点为直角顶点在第二象限作等腰直角△ABC.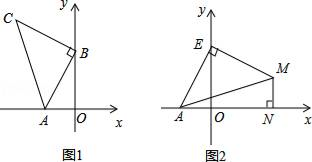

(1)、求C点的坐标；

(2)、在坐标平面内是否存在一点P，使△PAB与△ABC全等？若存在，求出P点坐标，若不存在，请说明理由；

(3)、如图2，点E为y轴正半轴上一动点，以E为直角顶点作等腰直角△AEM，过M作MN⊥x轴于N，求OE﹣MN的值.

查看试题解析

初中数学苏科版八年级上学期期末复习专题（9） 平面直角坐标系

一、单选题

二、填空题

三、综合题

初中数学苏科版八年级上学期期末复习专题（9）平面直角坐标系