安徽合肥瑶海三十八中2020-2021学年九年级上学期数学12月月考试卷
试卷更新日期:2020-12-18 类型:月考试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
-
1. 如果a是锐角,且cosa= ,那么sina的值是( )A、 B、 C、 D、2. 下列判断正确的是( )A、不全等的三角形一定不是相似三角形; B、不相似的三角形一定不是全等三角形; C、相似三角形一定不是全等三角形; D、全等三角形不一定是相似三角形3. 如图,点D在△ABC的边AC上,添加下列一个条件仍不能判断△ADB与△ABC相似的是( )
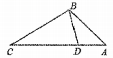 A、∠ABD=∠C B、∠ADB=∠ABC C、AB2=AD·AC D、BC2=CD·AC4. 若x1、x2(x1<x2)是方程(x-a)(x-b)=1(a<b)的两个根,则实数x1、x2、a、b的大小关系为( )A、x1<a<b<x2 B、x1<a<x2<b C、x1<x2<a<b D、a<x1<b<x25. 已知在△ABC中,∠C=90°,设sinB=n,当∠B是最小的内角时,n 的取值范围是( )A、0<n< B、0<n< C、0<n< D、0<n<6. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则反比例函数y= 与一次函数y=bx-c在同一坐标系内的图象大致是( )
A、∠ABD=∠C B、∠ADB=∠ABC C、AB2=AD·AC D、BC2=CD·AC4. 若x1、x2(x1<x2)是方程(x-a)(x-b)=1(a<b)的两个根,则实数x1、x2、a、b的大小关系为( )A、x1<a<b<x2 B、x1<a<x2<b C、x1<x2<a<b D、a<x1<b<x25. 已知在△ABC中,∠C=90°,设sinB=n,当∠B是最小的内角时,n 的取值范围是( )A、0<n< B、0<n< C、0<n< D、0<n<6. 二次函数y=ax2+bx+c(a≠0)的图象如图所示,则反比例函数y= 与一次函数y=bx-c在同一坐标系内的图象大致是( ) A、
A、 B、
B、 C、
C、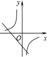 D、
D、 7. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BD交于点F,则S△DEF:S△ADF:S△ABF等于( )
7. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连结AE、BD交于点F,则S△DEF:S△ADF:S△ABF等于( )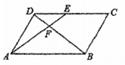 A、2:3:5 B、4:9:25 C、2:5:25 D、4:10:258. 如图,在△ABC中,CD平分∠ACB,过D作BC的平行线交AC于M,若BC=m,AC=n,则DM=( )
A、2:3:5 B、4:9:25 C、2:5:25 D、4:10:258. 如图,在△ABC中,CD平分∠ACB,过D作BC的平行线交AC于M,若BC=m,AC=n,则DM=( )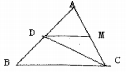 A、 B、 C、 D、9.
A、 B、 C、 D、9.如图,已知在Rt△ABC中,∠ABC=90°,点D沿BC自B向C运动(点D与点B、C不重合),作BE⊥AD于E,CF⊥AD于F,则BE+CF的值( )
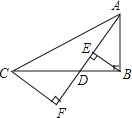 A、不变 B、增大 C、减小 D、先变大再变小10. 如图,在梯形ABCD中,AB=BC=10cm,CD=6cm,∠C=∠D-90°,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA、AD、DC运动,点Q沿BC、CD运动,P点与Q点相遇时停止,设P、Q同时从点B出发x秒时,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x之间的函微关系的大致图象为( )
A、不变 B、增大 C、减小 D、先变大再变小10. 如图,在梯形ABCD中,AB=BC=10cm,CD=6cm,∠C=∠D-90°,动点P、Q同时以每秒1cm的速度从点B出发,点P沿BA、AD、DC运动,点Q沿BC、CD运动,P点与Q点相遇时停止,设P、Q同时从点B出发x秒时,P、Q经过的路径与线段PQ围成的图形的面积为y(cm2),则y与x之间的函微关系的大致图象为( ) A、
A、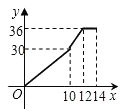 B、
B、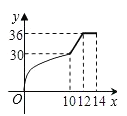 C、
C、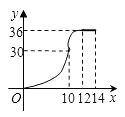 D、
D、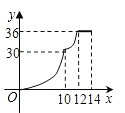
二、填空题(本大题共4小题,每小题5分,满分20分)
-
11. 若点A(2,m)在函数y=x2-1的图像上,则A点的坐标是12. 如图,在△ABC中,若∠A=30°,∠B=45°,AC= ,则BC=
 13. 如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,.设AB=xm,长方形的面积为ym2 , 要使长方形的面积最大,其边长x应为
13. 如图所示,在一个直角三角形的内部作一个长方形ABCD,其中AB和BC分别在两直角边上,.设AB=xm,长方形的面积为ym2 , 要使长方形的面积最大,其边长x应为 14. 设OABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1 , 相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……;依此类推,则Sn可表示为 (用含n的代数式表示,其中n为正整数)
14. 设OABC的面积为1,如图①将边BC、AC分别2等份,BE1、AD1 , 相交于点O,△AOB的面积记为S1;如图②将边BC、AC分别3等份,BE1、AD1相交于点O,△AOB的面积记为S2;……;依此类推,则Sn可表示为 (用含n的代数式表示,其中n为正整数)
三、(本大题共2小题, 每小题8分,满分16分)
-
15. 计算:16. 已知线段a、b、c满足a :b:c=3:2:6 ,且a+ 2b+c=26.(1)、求a、b、c的值;(2)、若线段x是线段a、b的比例中项,求x;
四、(本大题共2小题,每小题8分,满分16分)
-
17. 如图,Rt△ABC中斜边AB上一点M,MN⊥AB交AC于N,若AM=3厘米,AB:AC=5:4,求MN的长。
 18. 如图,在矩形ABCD中,E是AD边上的一点,BE⊥AC,垂足为点F。求证:△AEF∽△CAB.
18. 如图,在矩形ABCD中,E是AD边上的一点,BE⊥AC,垂足为点F。求证:△AEF∽△CAB.
五、(本大题共2小题, 每小题10分,满分20分)
-
19. 如图,两幢建筑物AB和CD,AB⊥BD,CD⊥BD,AB=15m, CD=20m。AB和CD之闻有一景观池,小双在A点测得池中喷泉处E点的俯角为42°,在C点测得E点的俯角为45°,点B、E、D在同一直线上。求两幢建筑物之间的距离BD.(结果精确到0.1m)[参考数据: sin42°=0.67,cos42°=0.74,tan42°=0。90]
 20. 如图,已知平行四边形ABCD的属长为8cm,∠B=30°,若边长AB=x(cm).
20. 如图,已知平行四边形ABCD的属长为8cm,∠B=30°,若边长AB=x(cm). (1)、求□ABCD的面积y(cm2)与x的函数关系式,并写出自变量x的取值范围;(2)、当x取什么值时,y的值最大?并求最大值;
(1)、求□ABCD的面积y(cm2)与x的函数关系式,并写出自变量x的取值范围;(2)、当x取什么值时,y的值最大?并求最大值;六、本题12分
-
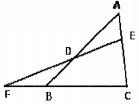
21. 如图已知△ABC中,点D、E分别在边AB、AC上,且AD:DB=3:2,AE:EC=1:2,直线ED和CB的延长线交于点F,求FB:BC.
七、本题12分
-
22. 如图,在直角坐标系xOy中,二次函数y=x2+(2k- 1)x+k+1的图象与x轴相交于O、A两点
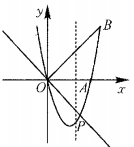 (1)、求这个二次函数的解析式;(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;(3)、对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由
(1)、求这个二次函数的解析式;(2)、在这条抛物线的对称轴右边的图象上有一点B,使△AOB的面积等于6,求点B的坐标;(3)、对于(2)中的点B,在此抛物线上是否存在点P,使∠POB=90°?若存在,求出点P的坐标,并求出△POB的面积;若不存在,请说明理由八、本题14分
-
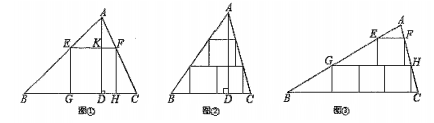
23. 如图①,一块材料的形状是锐角三角形ABC,边BC=120mm,高AD-80mm.把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB.AC上,这个正方形零件的边长是多少?
 (1)、【初步思考:】
(1)、【初步思考:】试计算出正方形零件的边长;
(2)、【深入探究】李华同学通过探究发现如果要把△ABC按照图②加工成三个相同大小的正方形零件,△ABC的边BC与高AD需要满足一定的数量关系,则这一数量关系是(直接写出结论,不用说明理由);
(3)、若△ABC可以按照图③加工成四个大小相同的正方形,且∠B=30°, 求证:AB=BC.
-
-