四川省达州市开江县2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-12-18 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣3的相反数是（）

A、 $- \frac{1}{3}$ B、 $\frac{1}{3}$ C、 $- 3$ D、 $3$

查看试题解析
2. 下面四个立体图形，从正面、左面、上面对空都不可能看到长方形的是 $($ 　　 $)$

A、 B、 C、 D、

查看试题解析
3. 2019年上半年，达州市地区生产总值约为880亿元，用科学记数法表示880亿元为（　　）

A、8.8×10² B、8.8×10⁹ C、8.8×10¹⁰ D、8.8×10¹¹

查看试题解析
4. 为了了解我县参加中考的6000名学生的体重情况，随机抽取了其中200名学生的体重进行统计分析．下面叙述正确的是（　　）

A、6000名学生是总体 B、200名学生的体重是总体的一个样本 C、每名学生是总体的一个个体 D、以上调查是普查

查看试题解析
5. 下列说法中正确的是（　　）

A、直线比射线长 B、AB＝BC，则点B是线段AC的中点 C、平角是一条直线 D、两条直线相交，只有一个交点

查看试题解析
6. 在代数式： $\frac{2}{n}$ ，3m﹣1，﹣2² ， $\frac{b^{2}}{4}$ ，2πa中，单项式的个数有（　　）

A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 根据流程图中的程序，当输出数值y为 $\frac{19}{4}$ 时，输入的数值x为（　　）

A、 $\frac{1}{2}$ B、﹣ $\frac{1}{2}$ C、﹣ $\frac{1}{2}$ 或 $\frac{1}{2}$ D、 $\frac{59}{5}$

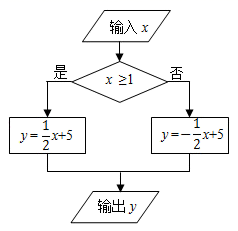查看试题解析
8. 设有x个人共种a棵树苗，如果每人种6棵，则剩下4棵树苗未种；如果每人种8棵，则缺2棵树苗．根据题意，列方程正确的是（　　）

A、 $\frac{x}{6}$ ﹣4＝ $\frac{x}{8}$ +2 B、 $\frac{x}{6}$ +4＝ $\frac{x}{8}$ ﹣2 C、 $\frac{a + 4}{6}$ ＝ $\frac{a - 4}{8}$ D、 $\frac{a - 4}{6}$ ＝ $\frac{a + 2}{8}$

查看试题解析
9. 若x＝|﹣3|，|y|＝2，则x﹣2y＝（　　）

A、﹣7 B、﹣1 C、﹣7或1 D、7或﹣1

查看试题解析
10. 如图所示，某公司有三个住宅区，A，B，C各区分别住有职工30人，15人，10人，且这三点在一条大道上（A，B，C三点共线），已知AB＝100米，BC＝200米.为了方便职工上下班，该公司的接送车打算在此间只设一个停靠点，为使所有的人步行到停靠点的路程之和最小，那么该停靠点的位置应设在（）

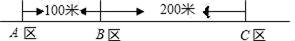A、点A B、点B C、A，B之间 D、B，C之间

查看试题解析

二、填空题

11. 比较大小： $- \frac{4}{3}$ $- \frac{3}{4}$ ．

查看试题解析
12. 若 $\frac{1}{3}$ $x^{1 - 2 m}$ $y$ 与﹣2 $x^{5} y^{3 n - 2}$ 是同类项，则n﹣2m＝．

查看试题解析
13. 若(m﹣2)x^|m|^﹣¹＝3是关于x的一元一次方程，则m的值是．

查看试题解析
14. 小明家有一个如图的无盖长方体纸盒，现沿着该纸盒的棱将纸盒剪开，得到其平面展开图 $.$ 若长方体纸盒的长、宽、高分别是a，b， $c ($ 单位：cm， $a > b > c) .$ 则它的展开图周长最大时，用含a，b，c的代数式表示最大周长为cm．

查看试题解析
15. 设一列数a₁ ， a₂ ， a₃ ， …，a₂₀₂₀中任意三个相邻数之和都是50．已知a₃＝4+x，a₁₀₀＝19，a₁₀₂₈＝2x，那么a₂₀₁₉＝．

查看试题解析
16. 如图，将长方形纸条的一部分CDEF沿EF折叠到GHEF的位置．若∠HEF＝65°，则∠AEH的度数为．

查看试题解析

三、解答题

17. 计算

(1)、﹣36×（ $\frac{3}{4} - \frac{5}{6} - \frac{1}{12}$ ）+（﹣2）³

(2)、﹣1²﹣（﹣3）³+|﹣5|÷ $\frac{1}{5}$

查看试题解析
18. 解方程

(1)、3x﹣2（9﹣x）＝﹣3

(2)、 $\frac{2 x - 1}{6} - x = \frac{x + 2}{3}$

查看试题解析
19. 化简求值：已知a、b、c满足（a+2）²+|b﹣1|＝0，求代数式5a²b+4ab﹣[3ab²﹣2（a²b﹣2ab）]的值．

查看试题解析
20. 某校为了了解本校七年级学生的视力情况（视力情况分为：不近视，轻度近视，中度近视，重度近视），随机对七年级的部分学生进行了抽样调查，将调查结果进行整理后，绘制了如下不完整的统计图，其中中度近视人数是不近视与重度近视人数之和的一半．

请你根据以上信息解答下列问题：

(1)、求本次调查的学生人数；

(2)、补全条形统计图．在扇形统计图中，求“中度近视”对应扇形的圆心角的度数；

(3)、若该校七年级学生有1200人，请你估计该校七年级近视（包括轻度近视，中度近视，重度近视）的学生大约有多少人？

查看试题解析
21. 如图所示，B在线段AC上，E在线段BC上，D是线段AB的中点若BC＝3AB，BE＝2EC，且DE＝7.5．求AC的长．

查看试题解析
22. 阅读材料：
我们知道，2x+3x﹣x＝（2+3﹣1）x＝4x，类似地，我们把（a+b）看成一个整体，则2（a+b）+3（a+b）﹣（a+b）＝（2+3﹣1）（a+b）＝4（a+b）．“整体思想”是中学数学解题中的一种重要的思想方法，它在多项式的化简与求值中应用极为广泛．

尝试应用：

(1)、把（x﹣y）²看成一个整体，求将2（x﹣y）²﹣5（x﹣y）²+（x﹣y）²合并的结果；

(2)、已知2m﹣3n＝4，求代数式4m﹣6n+5的值；
拓广探索

(3)、已知a﹣2b＝5，b﹣c＝﹣3，3c+d＝9，求（a+3c）﹣（2b+c）+（b+d）的值．

查看试题解析
23. 如图，数轴上的三点A、B、C分别表示有理数a、b、c，且|a|＞|c|＞|b|．

(1)、化简|a+c|﹣2|c﹣b|；

(2)、若b的倒数是它本身，且AB：BO：OC＝6：2：3，求（1）中代数式的值．

查看试题解析

24. 根据国家发改委实施“阶梯电价”的有关文件要求，某县结合地方实际，决定对居民生活用电实行“阶梯电价”收费，具体收费标准见下表

一户居民一个月用电量的范围	电费价格（单位：元/千瓦•时）
不超过150千瓦•时的部分	a
超过150千瓦•时，但不超过230千瓦•时的部分	b
超过230千瓦•时的部分	a+0.33

2019年10月份，该县居民甲用电100千瓦•时，交费64元；居民乙用电200千瓦•时，交费134.5元．

(1)、根据题意，求出上表中a和b的值；

(2)、实行“阶梯电价”收费以后，该县居民当月用电多少千瓦•时时，其当月的平均电价为0.67元？

查看试题解析

25. 如图，以直线AB上一点O为端点作射线OC，使∠AOC＝65°，将一个直角三角形的直角顶点放在点O处.（注：∠DOE＝90°）

(1)、如图①，若直角三角板DOE的一边OD放在射线OA上，则∠COE＝；

(2)、如图②，将直角三角板DOE绕点O顺时针方向转动到某个位置，若OC恰好平分∠AOE，求∠COD的度数；

(3)、如图③，将直角三角板DOE绕点O任意转动，如果OD始终在∠AOC的内部，试猜想∠AOD和∠COE有怎样的数量关系？并说明理由.

查看试题解析