四川省成都市新都区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-12-18 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣（﹣ $\frac{1}{3}$ ）的相反数是（　　）

A、3 B、﹣3 C、 $\frac{1}{3}$ D、﹣ $\frac{1}{3}$

查看试题解析
2. 某正方体的每个面上都有一个汉字，如图是它的一种展开图，那么在原正方体中，与“国”字所在面相对的面上的汉字是（）

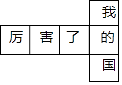A、厉 B、害 C、了 D、我

查看试题解析
3. 据新浪网报道：2019年参加国庆70周年大阅兵和后勤保障总人数多达98800人次，98800用科学记数法表示为（　　）

A、98.8×10³ B、0.988×10⁵ C、9.88×10⁴ D、9.88×10⁵

查看试题解析
4. 如图，经过刨平的木板上的A，B两个点，能弹出一条笔直的墨线，而且只能弹出一条墨线，能解释这一实际应用的数学知识是（）

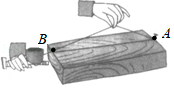A、两点之间，线段最短 B、两点确定一条直线 C、垂线段最短 D、在同一平面内，过一点有且只有一条直线与已知直线垂直

查看试题解析
5. 下列各组整式中，不属于同类项的是（　　）

A、﹣1和2 B、 $\frac{1}{2} x^{2} y$ 和x²y C、a²b和﹣b²a D、abc和3cab

查看试题解析
6. 用一副三角板拼成的图形如图所示，其中B，C，D三点在同一条直线上.则图中∠ACE的大小为（　　）

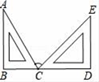A、45° B、60° C、75° D、105°

查看试题解析
7. 若 $x = 1$ 是方程 $2 x + a = 0$ 的解，则a的值是（）

A、 $1$ B、 $2$ C、 $- 1$ D、 $- 2$

查看试题解析
8. 2019年某市有11.7万名初中毕业生参加升学考试，为了了解这11.7万学生的数学成绩，从中抽取5000名学生的数学成绩进行统计，这个问题中一个样本是（　　）

A、11.7万名考生 B、5000名考生 C、5000名考生的数学成绩 D、11.7万名考生的数学成绩

查看试题解析
9. 已知 $a$ 、 $b$ 、 $c$ 三个数在数轴上对应的点如图所示，下列结论错误的是（）

A、 $a + c < 0$ B、 $b - c > 0$ C、 $c < - b < - a$ D、 $- b < a < - c$

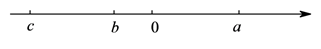查看试题解析
10. 某市按以下规定收取每月水费：若每月每户不超过20立方米，则每立方米按1.2元收费，若超过20立方米则超过部分每立方米按2元收费、如果某户居民在某月所交水费的平均水价为每立方米1.5元，那么这个月共用多少立方米的水设这个月共用x立方米的水，下列方程正确的是（）

A、1.2×20+2（x﹣20）＝1.5x B、1.2×20+2x＝1.5x C、 $\frac{1.2 + 2}{2} x = 1.5 x$ D、2x﹣1.2×20＝1.5x

查看试题解析

二、填空题

11. 关于x的多项式4x²ⁿ⁺¹﹣2x²﹣3x+1是四次多项式，则n＝．

查看试题解析
12. 9时45分时，时钟的时针与分针的夹角是.

查看试题解析
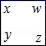13. 若“方框” 表示运算x﹣y+z+w ，则“方框” 的运算结果是＝．

查看试题解析
14. 如图所示，B、C是线段AD上任意两点，M是AB的中点，N是CD的中点，若MN＝6，BC＝2，则AD的长为．

查看试题解析
15. 已知（k²﹣1）x²﹣（k+1）x+10＝0是关于x的一元一次方程，则k的值为．

查看试题解析
16. 已知有理数a ， b ， c在数轴上的对应位置如图所示，则|a﹣b|﹣2|b﹣c|﹣|a﹣1|化简后的结果是．

查看试题解析
17. 已知多项式3x²+my﹣8与多项式﹣nx²+2y+7的差中，不含有x、y ，则n^m+mn＝．

查看试题解析
18. 如图，已知∠AOB＝40°，自O点引射线OC ，若∠AOC：∠COB＝2：3，OC与∠AOB的平分线所成的角的度数为．

查看试题解析
19. 如图所示，将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为a₁ ，第2幅图形中“●”的个数为a₂ ，第3幅图形中“●”的个数为a₃ ， …，以此类推，则 $\frac{1}{a_{1}} + \frac{1}{a_{2}} + \frac{1}{a_{3}} + \dots + \frac{1}{a_{10}}$ 的值为．

查看试题解析

三、解答题

20.

(1)、计算：（﹣3）²÷（1 $\frac{1}{2}$ ）²+（﹣4 $\frac{1}{2}$ ）× $\frac{1}{3}$ ．

(2)、解方程 $\frac{2 x - 1}{3} + \frac{x + 1}{2} = 2 x - \frac{2}{3}$ ．

查看试题解析
21. 先化简，再求值：﹣2（xy²+3xy）+3（1﹣xy²）﹣1，其中x＝ $\frac{1}{5}$ ，y＝﹣1．

查看试题解析
22. 一个几何体是由若干个棱长为1的小正方体堆积而成的，从不同方向看到的几何体的形状图如下．

(1)、在从上面看得到的形状图中标出相应位置小正方体的个数；

(2)、这个几何体的表面积是．

查看试题解析
23. 对垃圾进行分类投放，能有效提高对垃圾的处理和再利用，减少污染，保护环境．为了调查同学们对垃圾分类知识的了解程度，增强同学们的环保意识，普及垃圾分类及投放的相关知识，某校数学兴趣小组的同学设计了“垃圾分类知识及投放情况”问卷，并在本校随机抽取部分同学进行问卷测试，把测试成绩分成“优、良、中、差”四个等级，绘制了如下不完整的统计图：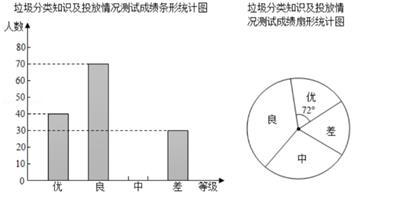

根据以上统计信息，解答下列问题

(1)、求成绩是“优”的人数占抽取人数的百分比；

(2)、求本次随机抽取问卷测试的人数

(3)、请把条形统计图补充完整

(4)、若该校学生人数为3000人，请估计成绩是“优”和“良”的学生共有多少人?

查看试题解析
24. 如图，OA的方向是北偏东15°，OB的方向是西偏北50°，OD是OB的反向延长线．

(1)、若∠AOC＝∠AOB ，求OC的方向．

(2)、在（1）问的条件下，作∠AOD的角平分线OE ，求∠COE的度数．

查看试题解析
25. 在天府新区的建设中，现要把176吨物资从某地运往华阳的甲、乙两地，用大、小两种货车共18辆，恰好能一次性运完这批物资．已知这两种货车的载重量分别为12吨/辆和8吨/辆，运往甲、乙两地的运费如下表：

运往地

车型

甲地（元/辆）

乙地（元/辆）

大货车

640

680

小货车

500

560

(1)、求这两种货车各用多少辆？

(2)、如果安排10辆货车前往甲地，其余货车前往乙地，设前往甲地的大货车为a辆，运往甲、乙两地的总运费为w元，求出w与a的关系式；

(3)、在（2）的条件下，若运往甲地的物资为100吨，请求出安排前往甲地的大货车多少辆，并求出总运费．

查看试题解析
26. 已知A＝2a²+3ab﹣2a﹣1，B＝﹣a²+ $\frac{1}{2} a b + \frac{2}{3}$

(1)、当a＝﹣1，b＝﹣2时，求4A﹣（3A﹣2B）的值；

(2)、若（1）中式子的值与a的取值无关，求b的值.

查看试题解析
27. 如图，直线1上有A ， B两点，AB=12cm ，点O是线段AB上的一点，OA=2OB ．

(1)、OA=cm ， OB=cm；

(2)、若点C是线段AB上一点（点C不与点AB重合），且满足AC=CO+CB ，求CO的长；

(3)、若动点P ， Q分别从A ， B同时出发，向右运动，点P的速度为2cm/s ，点Q的速度为1cm/s ．设运动时间为t（s），当点P与点Q重合时，P ， Q两点停止运动．求当t为何值时，2OP-OQ=4（cm）；

查看试题解析
28. 已知OC是∠AOB内部的一条射线，M ， N分别为OA ， OC上的点，线段OM ， ON同时分别以30°/s ， 10°/s的速度绕点O逆时针旋转，设旋转时间为t秒．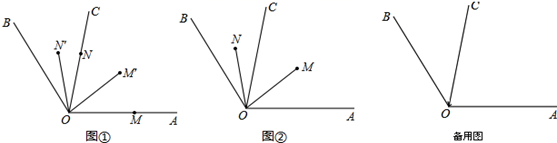

(1)、如图①，若∠AOB＝120°，当OM、ON逆时针旋转到OM′、ON′处，若OM ， ON旋转时间t为2时，则∠BON′+∠COM′＝°；

(2)、若OM′平分∠AOC ， ON′平分∠BOC ，求∠M′ON′的值；

(3)、如图②，若∠AOB＝4∠BOC ， OM ， ON分别在∠AOC ， ∠BOC内部旋转时，请猜想∠COM与∠BON的数量关系，并说明理由．

(4)、若∠AOC＝80°，OM ， ON在旋转的过程中，当∠MON＝20°，t＝．

查看试题解析