四川省成都市金牛区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-12-18 类型：期末考试

进入出卷网下载

一、单选题

1. $| - \frac{1}{3} |$ 的相反数是（）

A、 $\frac{1}{3}$ B、 $- \frac{1}{3}$ C、3 D、-3

查看试题解析
2. 下列几何体中，是圆锥的为（）

A、 B、 C、 D、

查看试题解析
3. 电影《流浪地球》中的行星发动机利用重核聚变技术，可以直接利用石头作为燃料，每座发动机产生150亿吨推力，请用科学记数法表示150亿为（）

A、 $150 \times 10^{9}$ B、 $1.5 \times 10^{10}$ C、 $1.5 \times 10^{11}$ D、 $1.5 \times 10^{12}$

查看试题解析
4. 下列计算正确的是（）

A、 $7 a + a = 7 a^{2}$ B、 $3 x^{2} y - 2 y x^{2} = x^{2} y$ C、 $5 y - 3 y = 2$ D、 $3 a + 2 b = 5 a b$

查看试题解析
5. 由几个相同的小正方体搭成的几何体的视图如图所示，则搭成这个几何体的小正方体的个数是（）

A、5 B、6 C、7 D、8

查看试题解析
6. 如果 $x = y$ ，那么根据等式的性质下列变形正确的是（　　）

A、 $x + y = 0$ B、 $\frac{x}{5} = \frac{5}{y}$ C、 $2 - x = 2 - y$ D、 $x + 7 = y - 7$

查看试题解析
7. 下列调查方式合适的是（）

A、为了了解市民对70周年国庆大阅兵的感受，小华在某校随机采访了8名初一学生； B、为了了解全校学生用于做数学作业的时间，小民同学在网上向6位好友做了调查； C、为了了解全国青少年儿童的睡眠时间，统计人员采用了普查的方式； D、为了了解“北斗导航”卫星零部件的状况，检测人员采用了普查的方式；

查看试题解析
8. 如图，OC是∠AOB的平分线，OD平分∠AOC，且 $∠ A O B = 100^{\circ}$ ，则∠COD的度数是（）

A、75° B、50° C、25° D、20°

查看试题解析
9. 下列说法正确的个数为（　　）
⑴过两点有且只有一条直线

⑵连接两点的线段叫做两点间的距离

⑶两点之间的所有连线中，线段最短

⑷直线AB和直线BA表示同一条直线．

A、1 B、2 C、3 D、4

查看试题解析
10. 已知一件标价为400元的上衣按八折销售，仍可获利50元.设这件上衣成本价为x元，根据题意，那么下面所列方程正确的是（）

A、400×8-x = 50 B、400×0.8-x = 50 C、400×8+x = 50 D、400×0.8+x = 50

查看试题解析

二、填空题

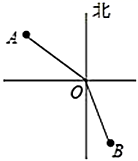
11. 已知x=5是关于x的方程ax+8=20-a的解，则a的值是．

查看试题解析
12. 已知 $2 x^{2 m} y^{3}$ 和 $- \frac{1}{4} x^{6} y^{1 - n}$ 是同类项，则m-n的值是.

查看试题解析
13. 已知 $| x + 3 | + {(y - 2)}^{2} = 0$ ，则x+y= ．

查看试题解析
14. 在灯塔 $O$ 处观测到轮船 $A$ 位于北偏西 $54 °$ 的方向，同时轮船 $B$ 在南偏东 $15 °$ 的方向，那么 $∠ A O B$ 的大小为.

查看试题解析
15. 如果方程 $11 x + 2 m = 37$ 与方程 $\frac{11}{3} x - 3 = 2 \frac{2}{3}$ 的解相同，那么m=。

查看试题解析
16. 已知a、b互为相反数且a≠0，c、d互为倒数，|m|是最小的正整数，则 $m + \frac{2019 (a + b)}{2020} - c d$ 的值为.

查看试题解析
17. 若规定 $f (x) ＝ 5 - x + | x - 5 |$ ，例如 $f (1) ＝ 5 - 1 + | 1 - 5 | ＝ 8$ ，则 $f (1) + f (2) + f (3) + \dots \dots + f (2020)$ ＝.

查看试题解析
18. 如图1，在长方形纸片ABCD中，E点在边AD上，F、G分别在边AB、CD上，分别以EF、EG为折痕进行折叠并压平，点A、D的对应点分别是点A′和点D′，若ED′平分∠FEG ，且 $E D^{'}$ 在 $∠ A^{'} E F$ 内部，如图2，设∠A′ED'=n°，则∠FE D′的度数为(用含n的代数式表示)．

查看试题解析
19. 如图所示，甲、乙两人沿着边长为10m的正方形，按A→B→C→D→A…的方向行走，甲从A点以5m/分钟的速度，乙从B点以8m/分钟的速度行走，两人同时出发，当甲、乙第20次相遇时，它们在边上。

查看试题解析

三、解答题

20.

(1)、 $2 \times (- 5) + 4 - 3 \div \frac{1}{2}$

(2)、 ${(- 1)}^{4} + \frac{1}{30} - (- \frac{2}{3} + \frac{3}{5}) \div (- 2)$

查看试题解析
21. 解方程

(1)、 $4 x - 3 (2 - 4 x) = 26$

(2)、 $\frac{3 x - 1}{2} - \frac{2 x - 2}{3} = - 1$

查看试题解析
22. 先化简，再求值： $3 (x^{2} - x y - 2 y) - 2 (x^{2} - 3 y)$ ，其中 $x = - 1$ ， $y = 2$ .

查看试题解析
23. 2019年11月，我区组织了一次职工篮球联赛，比赛分初赛阶段和决赛阶段，在初赛阶段中，每队有10场比赛，每场比赛都要分出胜负，每队胜一场得2分，输一场得1分，积分超过15分才能获得决赛资格.

(1)、若乙队初赛获得4场胜利，问乙队是否有资格参加决赛？请说明理由.

(2)、已知甲队在初赛阶段的积分为18分，求甲队初赛阶段胜、负各多少场；

查看试题解析
24. 我区的数学爱好者申请了一项省级课题——《中学学科核心素养理念下渗透数学美育的研究》，为了了解学生对数学美的了解情况，随机抽取部分学生进行问卷调查，按照“理解、了解、不太了解、不知道”四个类型，课题组绘制了如下两幅不完整的统计图，请根据统计图中提供的信息，回答下列问题：

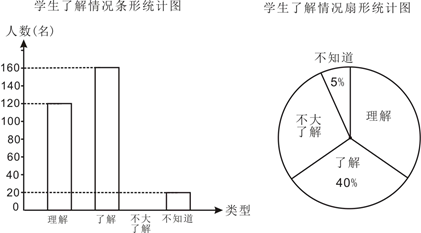(1)、本次调查共抽取了多少名学生？并补全条形统计图；

(2)、在扇形统计图中，“理解”所占扇形的圆心角是多少度？

(3)、我区七年级大约8000名学生，请估计“理解”和“了解”的共有学生多少名？

查看试题解析
25. 已知线段AB=m(m为常数)，点C为直线AB上一点（不与点A、B重合），点M、N分别在线段BC、AC上，且满足CN=3AN ， CM=3BM.

(1)、如图，当点C恰好在线段AB中点，且m=8时，则MN=；

(2)、若点C在点A左侧，同时点M在线段AB上(不与端点重合)，请判断CN+2AM -2MN的值是否与m有关？并说明理由.

(3)、若点C是直线AB上一点（不与点A、B重合），同时点M在线段AB上(不与端点重合)，求MN长度 (用含m的代数式表示).

查看试题解析
26. 已知关于x的整式 $M = x^{2} + 6 a x - 3 x + 2$ ，整式N= $- 2 x^{2} + 4 a x - 2 x + 2$ ，若a是常数，且2M+N的值与x无关。

(1)、求a的值；

(2)、若b为整数，关于x的一元一次方程 $b x + b - 3 = 0$ 的解是正整数，求 $a^{b}$ 的值.

查看试题解析
27. 某公司销售甲、乙两种运动鞋，2018年这两种鞋共卖出11000双。2019年甲种运动鞋卖出的数量比2018年增加6%，乙种运动鞋卖出的数量比2018年减少5%，且这两种鞋的总销量增加了2%．

(1)、求2018年甲、乙两种运动鞋各卖了多少双？

(2)、某制鞋厂组织工人生产甲、乙两种运动鞋。原计划安排 $\frac{2}{3}$ 的工人生产甲种运动鞋，现抽调其中的16人去生产乙种运动鞋，已知每位工人一天可生产甲种运动鞋6双或乙种运动鞋4双，若调配后制成的两种运动鞋数量相等，求该鞋厂工人的人数。

查看试题解析
28. 已知 $∠ AOB = 90 °$ ， $∠ COD = 60 °$ ，按如图1所示摆放，将OA、OC边重合在直线MN上，OB、OD边在直线MN的两侧；

(1)、保持 $∠ AOB$ 不动，将 $∠ COD$ 绕点O旋转至如图2所示的位置，则① $∠ AOC + ∠ BOD$ =；② $∠ BOC - ∠ AOD$ =；

(2)、若 $∠ COD$ 按每分钟 $5 °$ 的速度绕点O逆时针方向旋转， $∠ AOB$ 按每分钟 $2 °$ 的速度也绕点O逆时针方向旋转，OC旋转到射线ON上时都停止运动，设旋转t分钟，计算 $∠ MOC - ∠ AOD$ (用t的代数式表示)。

(3)、保持 $∠ AOB$ 不动，将 $∠ COD$ 绕点O逆时针方向旋转 $n ° (n \leq 360)$ ，若射线OE平分 $∠ AOC$ ，射线OF平分 $∠ BOD$ ，求 $∠ EOF$ 的大小；

查看试题解析