四川省成都市简阳市2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-12-18 类型:期末考试
一、单选题
-
1. 下图中的图形绕虚线旋转一周,可得到的几何体是( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列各数中,非正数有( )
2. 下列各数中,非正数有( ), , , , , , ,
A、 个 B、 个 C、 个 D、 个3. 已知 , ,且 ,则 ( )A、 B、 C、 或- D、4. 下列各组的两个数中,运算后结果相等的是( )
A、23和32 B、﹣33和(﹣3)3 C、﹣22和(﹣2)2 D、 和5. 核桃的单价为m元/千克,栗子的单价为n元/千克,买2千克核桃和3千克栗子共需( )A、(m+n)元 B、(3m+2n)元 C、(2m+3n)元 D、5(m+n)元6. 下列各组中的两项,不是同类项的是( )A、a2b与-3ab2 B、-x2y与2yx2 C、2πr与π2r D、35与537. 如图,下列结论中,不能说明射线 平分 的是( ) A、 B、 C、 D、8. 下列等式中不是一元一次方程的是( )A、 B、 C、 D、9. 下列方程的变形中正确的是( )A、由7x=4x-3移项得7x-4x=3 B、由 去分母得2(2x-1)=1+3(x-3) C、由2(2x-1)-3(x-3)=1去括号得4x-2-3x-9=1 D、由2(x+1)=x+7解得x=510. 如图所示的两个统计图,女生人数多的学校是( )
A、 B、 C、 D、8. 下列等式中不是一元一次方程的是( )A、 B、 C、 D、9. 下列方程的变形中正确的是( )A、由7x=4x-3移项得7x-4x=3 B、由 去分母得2(2x-1)=1+3(x-3) C、由2(2x-1)-3(x-3)=1去括号得4x-2-3x-9=1 D、由2(x+1)=x+7解得x=510. 如图所示的两个统计图,女生人数多的学校是( ) A、甲校 B、乙校 C、甲、乙两校女生人数一样多 D、无法确定
A、甲校 B、乙校 C、甲、乙两校女生人数一样多 D、无法确定二、填空题
-
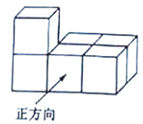
11. 下图是由六个棱长为 的正方体组成的几何体,则从上面看得到的平面图形的面积是.
 12. 全球每年大约有 的水从海洋和陆地转化为大气中的水汽,用科学记数法应该表示为 .13. 某商场把进价为 300 元的商品,按标价的八折出售,仍可获利 20% ,则商品的标价为.14. 如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为 .
12. 全球每年大约有 的水从海洋和陆地转化为大气中的水汽,用科学记数法应该表示为 .13. 某商场把进价为 300 元的商品,按标价的八折出售,仍可获利 20% ,则商品的标价为.14. 如图,将三个同样的正方形的一个顶点重合放置,那么∠1的度数为 .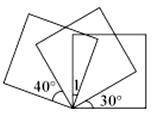 15. 已知a,b互为相反数,c,d互为倒数,x的绝对值是 ,则 的值为 .16. 对于有理数a,b,定义 ,则 化简后得.17. 如图,射线 的方向是北偏东 ,射线 的方向是北偏西 , , 是 的反向延长线.
15. 已知a,b互为相反数,c,d互为倒数,x的绝对值是 ,则 的值为 .16. 对于有理数a,b,定义 ,则 化简后得.17. 如图,射线 的方向是北偏东 ,射线 的方向是北偏西 , , 是 的反向延长线. (1)、射线 的方向是;(2)、 的度数是.18. 已知:1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52 , …,
(1)、射线 的方向是;(2)、 的度数是.18. 已知:1+3=4=22;1+3+5=9=32;1+3+5+7=16=42;1+3+5+7+9=25=52 , …,根据前面各式的规律,以下等式(n为正整数),
①1+3+5+7+9+…+(2n-1)=n2;
②1+3+5+7+9+…+(2n+3)=(n+3)2;
③1+3+5+7+9+…+2013=10072;
④101+…+2013=10072-502
其中正确的有个.
三、解答题
-
19. 计算(1)、计算:(2)、(3)、先化简,再求值:已知 ,求: 的值.20. 解方程(1)、(2)、21. 如图所示,圆柱的底面半径为3 cm,高为4 cm.若沿图中的线AB把圆柱的侧面展开,你认为会得到什么图形?请你求出这个侧面展开图的面积.
 22. 如图,OE为∠AOD的平分线,∠COD= ∠EOC,∠COD=15°,
22. 如图,OE为∠AOD的平分线,∠COD= ∠EOC,∠COD=15°,
求:
(1)、∠EOC的大小;(2)、∠AOD的大小23. 为了迎接 年高中招生考试,简阳市某中学对全校九年级学生进行了一次数学摸底考试,并随机抽取了部分学生的测试成绩作为样本进行分析,绘制成了如下两幅不完整的统计图,请根据图中所给出的信息,解答下列问题: (1)、在这次调查中,被抽取的学生的总人数为多少?(2)、请将表示成绩类别为“中”的条形统计图补充完整:(3)、在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角的度数是:(4)、学校九年级共有 人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?24. 某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.
(1)、在这次调查中,被抽取的学生的总人数为多少?(2)、请将表示成绩类别为“中”的条形统计图补充完整:(3)、在扇形统计图中,表示成绩类别为“优”的扇形所对应的圆心角的度数是:(4)、学校九年级共有 人参加了这次数学考试,估计该校九年级共有多少名学生的数学成绩可以达到优秀?24. 某超市为了回馈广大新老客户,元旦期间决定实行优惠活动.优惠一:非会员购物时,所有商品均可享受九折优惠;
优惠二:交纳200元会费成为该超市的会员,所有商品可享受八折优惠.
(1)、若用x表示商品价格,请你用含x的式子分别表示两种购物方式优惠后所花的钱数.(2)、当商品价格是多少元时,用两种方式购物后所花钱数相同?(3)、若某人计划在该超市购买一台价格为2700元的电脑,请分析选择哪种优惠方式更省钱.25. 当n等于 , , , 时,由白色小正方形和黑色小正方形组成的图形分别如图所示.则第n个图形中白色小正方形和黑色小正方形的个数总和等于,.(用n表示,n是正整数)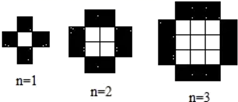 26. 已知:2x2+ax﹣y+6﹣bx2+3x﹣5y﹣1的值与x的取值无关,A=4a2﹣ab+4b2 , B=3a2﹣ab+3b2 , 先化简3A﹣[2(3A﹣2B)﹣3(4A﹣3B)]再求值.27. 在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.
26. 已知:2x2+ax﹣y+6﹣bx2+3x﹣5y﹣1的值与x的取值无关,A=4a2﹣ab+4b2 , B=3a2﹣ab+3b2 , 先化简3A﹣[2(3A﹣2B)﹣3(4A﹣3B)]再求值.27. 在解决数学问题的过程中,我们常用到“分类讨论”的数学思想,下面是运用分类讨论的数学思想解决问题的过程,请仔细阅读,并解答问题.(提出问题)三个有理数a、b、c满足 ,求 的值.
(解决问题)
解:由题意,得a、b、c三个有理数都为正数或其中一个为正数,另两个为负数,
①a、b、c都是正数,即 、 、 时,则 :
②当a、b、c中有一个为正数,另两个为负数时,不妨设 、 、 ,则, ,综上所述, 值为 或 .
(探究)请根据上面的解题思路解答下面的问题:
(1)、三个有理数a、b、c满足 ,求 的值;(2)、若a、b、c为三个不为0的有理数,且 ,求 的值.28. 如果一点在由两条公共端点的线段组成的一条折线上且把这条折线分成长度相等的两部分,这点叫做这条折线的“折中点”.如图,点D是折线A﹣C﹣B的“折中点”,请解答以下问题: (1)、当AC>BC时,点D在线段上; 当AC=BC时,点D与重合;当AC<BC时,点D在线段上;(2)、若AC=18cm,BC=10cm,若∠ACB=90°,有一动点P从C点出发,在线段CB上向点B运动,速度为2cm/s, 设运动时间是t(s), 求当t为何值,三角形PCD 的面积为10 ?(3)、若E为线段AC中点,EC=8cm,CD=6cm,求CB的长度.
(1)、当AC>BC时,点D在线段上; 当AC=BC时,点D与重合;当AC<BC时,点D在线段上;(2)、若AC=18cm,BC=10cm,若∠ACB=90°,有一动点P从C点出发,在线段CB上向点B运动,速度为2cm/s, 设运动时间是t(s), 求当t为何值,三角形PCD 的面积为10 ?(3)、若E为线段AC中点,EC=8cm,CD=6cm,求CB的长度.