四川省成都市高新区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-12-18 类型：期末考试

进入出卷网下载

一、单选题

1. ﹣3的绝对值是（）

A、﹣3 B、3 C、- $\frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
2. 下面四个几何体的视图中，从上面看是三角形的是(　　)

A、 B、 C、 D、

查看试题解析
3. 庆祝中华人民共和国成立70周年阅兵式于2019年10月1日在天安门广场隆重举行，此次阅兵约9万人参与演练及现场保障工作，将数据9万用科学记数法表示为(　　)

A、9×10³ B、9×10⁴ C、9×10⁵ D、9×10⁶

查看试题解析
4. 下列调查中，最适宜采用普查方式的是（　　）

A、对全国初中学生视力状况的调査 B、对“十一国庆”期间全国居民旅游出行方式的调查 C、旅客上飞机前的安全检查 D、了解某种品牌手机电池的使用寿命

查看试题解析
5. 下列计算正确的是(　　)

A、2a+3b=5ab B、2a²+3a²=5a⁴ C、2a²b+3a²b=5a²b D、2a²﹣3a²=﹣a

查看试题解析
6. 若x=5是方程ax﹣8=12的解，则a的值为(　　)

A、3 B、4 C、5 D、6

查看试题解析
7. 下列各式的值一定为正数的是(　　)

A、(a+2)² B、|a﹣1| C、a+1000 D、a²+1

查看试题解析
8. 下面的说法正确的是(　　)

A、有理数的绝对值一定比0大 B、有理数的相反数一定比0小 C、如果两个数的绝对值相等，那么这两个数相等 D、互为相反数的两个数的绝对值相等

查看试题解析
9. 如图，∠AOC和∠BOD都是直角，如果∠DOC=28°，那么∠AOB的度数是(　　)

A、118° B、152° C、28° D、62°

查看试题解析
10. 一家商店将某种服装按照成本价提高40%后标价，又以8折优惠卖出，结果每件仍获利15元，这种服装每件的成本是多少元？设这种服装每件的成本是x元，则根据题意列出方程正确的是(　　)

A、0.8×(1+40%)x=15 B、0.8×(1+40%)x﹣x=15 C、0.8×40%x=15 D、0.8×40%x﹣x=15

查看试题解析

二、填空题

11. | $- \frac{2}{5}$ |的相反数是， | $- \frac{2}{5}$ |的倒数是．

查看试题解析
12. 如图，点B在线段AC上，AB=4，BC=2，点M为线段AB中点，点N为线段BC中点，则线段MN的长度为．

查看试题解析
13. 数轴上与表示-1 的点距离 2 个单位长度的点所表示的数是.

查看试题解析
14. 一根长80cm的弹簧，一端固定．如果另一端挂上物体，那么在正常情况下物体的质量每增加1kg可使弹簧增长2cm ，正常情况下，当挂着xkg的物体时，弹簧的长度是cm ． (用含x的代数式表示)

查看试题解析
15. 若m²﹣2m+1=0，则代数式2m²﹣4m+2019的值为．

查看试题解析
16. 如图，将一个边长为1的正方形纸片分割成7个部分，部分1是边长为1的正方形纸片面积的一半，部分2是部分D面积的一半，部分3是部分2面积的一半，依此类推．阴影部分的面积是；受此启发，则 $\frac{1}{2} + \frac{1}{4} + \frac{1}{8} + \dots + \frac{1}{2^{6}}$ 的值为．

查看试题解析
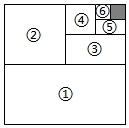17. 在学习了有理数的混合运算后，小明和小刚玩算“24点”游戏．游戏规则：从一副扑克牌(去掉大，小王)中任意抽取4张，根据牌面上的数字进行混合运算(每张牌必须用一次且只能用一次，可以加括号)，使得运算结果为24或﹣24．其中红色扑克牌代表负数，黑色扑克代表正数，J，Q ， K分别代表11，12，13．小明抽到的四张牌分别是黑桃1，黑桃3，梅花4，梅花6(都是黑色扑克牌)．小明凑成的等式为6÷(1﹣3÷4)=24，小亮抽到的四张牌分别是黑桃7、黑桃3、梅花7、梅花3(都是黑色扑克牌)：请写出小亮凑成的“24点”等式．

查看试题解析
18. 如图，都是由同样大小的黑棋子按一定规律摆出的图案，第1个图有2颗黑棋子，第2个图有7颗黑棋子，第3个图有14颗黑棋子…依此规律，第5个图有颗黑棋子，第n个图有颗棋子(用含n的代数式示)．

查看试题解析
19. [知识背景]：三角形是数学中常见的基本图形，它的三个角之和为180°．等腰三角形是一种特殊的三角形，如果一个三角形有两边相等，那么这个三角形是等腰三角形，相等的两边所对的角也相等．

如图1，在三角形ABC中，如果AB=AC ，那么∠B=∠C ．同样，如果∠B=∠C ，则AB=AC ，即这个三角形也是等腰三角形．

[知识应用]：如图2，在三角形ABC中，∠ACB=90°，∠ABC=30°，将三角形ABC绕点C逆时针旋转α(0°＜α＜60°)度(即∠ECB=α度)，得到对应的三角形DEC ， CE交AB于点H ，连接BE ，若三角形BEH为等腰三角形，则α=°．

查看试题解析

三、解答题

20. 计算题：

(1)、8+(﹣3)²×(﹣2)﹣(﹣3)

(2)、﹣1²﹣24×( $- \frac{1}{6} + \frac{2}{3} - \frac{3}{4}$ )

查看试题解析
21. 化简或化简求值：

(1)、化简：(2ab+a²b)+3(2a²b﹣5ab)；

(2)、先化简，再求值：(﹣x²+3xy﹣2y)﹣2( $- \frac{1}{2}$ x²+4xy $- \frac{3}{2}$ y²)，其中x=3，y=﹣2．

查看试题解析
22. 解方程：

(1)、4x﹣3(20﹣x)=3

(2)、 $\frac{y - 1}{2} =$ 2 $- \frac{y + 2}{5}$

查看试题解析
23. 英才中学为了解中考体育科目训练情况从全校九年级学生中随机抽取了部分学生进行一次中考体育科目测试(把测试结果分为四个等级．A级：优秀；B级：良好；C级：合格；D级：不合格)，并将测试结果绘成了如下两幅不完整的统计图．请根据统计图中的信息解答下列问题：

(1)、求本次抽样测试的学生人数是人．

(2)、图2中条形统计图C级的人数是人；

(3)、该校九年级有学生500名，如果全部参加这次中考体育科目测试，请估计不及格的人数约有多少人？

查看试题解析
24. 探索练习：某文艺团体为“希望工程”募捐组织了一场义演，共售出1000张票，其中成人票是每张8元，学生票是每张5元，筹得票款6950元．问成人票与学生票各售出多少张？

查看试题解析
25. 已知：点O为直线AB上一点，过点O作射线OC ，使∠AOC=70°．

(1)、如图1，若OD平分∠AOC ，求∠DOB的度数；

(2)、射线OM从OA出发，绕点O以每秒6°的速度逆时针旋转，同时，射线ON从OC出发绕点O以每秒4°的速度逆时针旋转，OM与ON同时出发(当ON首次与OB重合时，两条射线都停止运动)，设运动的时间为t秒．
(i)如图2，在整个运动过程中，当∠BON=2∠COM时，求t的值；

(ⅱ)如图3，OP平分∠AOM ， OQ平分∠BON ，是否存在合适的t ，使OC平分∠POQ ，若存在，求出t的值，若不存在，请说明理由．

查看试题解析
26.

(1)、若关于a ， b的多项式3(a²﹣2ab+b²)﹣(2a²﹣mab+2b²)中不含有ab项，求m的值．

(2)、已知两个有理数，y满足条件：|x|=7，|y|=4，x+y＞0，xy＜0，求x﹣y的值．

查看试题解析
27. 成都市民打车出行常用交通工具为出租车和滴滴快车．该市两种车的收费标准如下：
出租车：2千米以内9元；超过2千米的部分：2元/千米．

滴滴快车：里程费：1.6元/千米；时长费：18元/小时；远途费：0.8元/千米．(注：滴滴快车的收费由里程费、时长费、远途费三部分组成，其中里程费按行车的实际里程计算；时长费按照行车的实际时间计算；远途费的收取方式为：行车不超过8千米，不收远途费，超过8千米的，超过部分每千米加收0.8元)．假设打车的平均速度为30千米/小时．

(1)、小明家到学校4千米，乘坐出租车需要多少元？

(2)、设乘车路程为x(x＞2)千米，分别写出出租车和滴滴快车的应收费用(用含x的代数式表示)；

(3)、小方和爸爸从家去环球中心(家到环球中心的距离天于2千米)，乘坐滴滴快车比乘坐出租车节约2.4元，求小方家到环球中心的距离．

查看试题解析
28. 已知：数轴上点A、B、C表示的数分别为a、b、c ，点O为原点，且a、b、c满足(a﹣6)²+|b﹣2|+|c﹣1|=0．

(1)、直接写出a、b、c的值；

(2)、如图1，若点M从点A出发以每秒1个单位的速度向右运动，点N从点B出发以每秒3个单位的速度向右运动，点R从点C出发以每秒2个单位的速度向右运动，点M、N、R同时出发，设运动的时间为t秒，t为何值时，点N到点M、R的距离相等；

(3)、如图2，若点P从点A出发以每秒1个单位的速度向左运动，点Q从点B出发以每秒3个单位的速度向左运动，点P ， Q同时出发开始运动，点K为数轴上的一个动点，且点C始终为线段PK的中点，设运动时间为t秒，若点K到线段PC的中点D的距离为3时，求t的值．

查看试题解析