初中数学苏科版八年级上学期期末复习专题（8）实数

试卷更新日期：2020-12-18 类型：复习试卷

进入出卷网下载

一、单选题

1. 下列说法：
①实数和数轴上的点是一一对应的；②无理数是开方开不尽的数；③负数没有立方根；④16的平方根是±4，用式子表示是 $\sqrt{16}$ =±4；⑤某数的绝对值，相反数，算术平方根都是它本身，则这个数是0，其中错误的有（）

A、0个 B、1个 C、2个 D、3个

查看试题解析
2.
如图，数轴上点P表示的数可能是（）

A、 $\sqrt{10}$ B、 $\sqrt{2}$ C、 $\sqrt{3}$ D、 $\sqrt{5}$

查看试题解析
3. 如图，以数轴的单位长度线段为边作一个正方形，以表示数2的点为圆心，正方形对角线长为半径画弧，交数轴于点A，则点A表示的数是（）

A、 $- \sqrt{2}$ B、2 $- \sqrt{2}$ C、1 $- \sqrt{2}$ D、1+ $\sqrt{2}$

查看试题解析
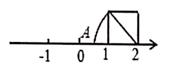4. 如图，数轴上与1、 $\sqrt{2}$ 两个实数对应的点分别为A、B ，点C与点B关于点A对称，则点C表示的数是（）

A、2 $-$ $\sqrt{2}$ B、 $\sqrt{2}$ $-$ 1 C、1 $-$ $\sqrt{2}$ D、2 $\sqrt{2}$ $-$ 2

查看试题解析
5.
正方形的网格中，每个小正方形的边长为1，则网格中三角形ABC中，边长是无理数的边数是（）

A、0 B、1 C、2 D、3

查看试题解析
6. 如图，直径为1个单位长度的圆从原点沿数轴向右滚动一周，圆上一点由原点到达点 $A$ ，下列说法正确的是（）

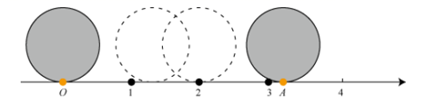A、点 $A$ 所表示的是 $π$ B、数轴上只有一个无理数 $π$ C、数轴上只有无理数没有有理数 D、数轴上的有理数比无理数要多一些

查看试题解析
7. 某种鲸的体重约为 $1.36 \times 10^{5} k g$ ，关于这个近似数，下列说法正确的是（）

A、精确到百分位 B、精确到0.01 C、精确到千分位 D、精确到千位

查看试题解析
8. 若是m+n+3的算术平方根，是m+2n的立方根，则B-A的立方根是（）

A、1 B、-1 C、0 D、无法确定

查看试题解析
9. 我们规定：a*b= $\frac{a + b}{2}$ ，则下列等式中对于任意实数a、b、c都成立的是（   ）
①a+（b*c）=（a+b）*（a+c）     ②a*（b+c）=（a+b）*c
③a*（b+c）=（a*b）+（a*c）     ④（a*b）+c= $\frac{a}{2}$ +（b*2c）

A、①②③ B、①②④ C、①③④ D、②④

查看试题解析
10. 若x为实数，记{x}=x-[x]（其中[x]表示不超过x的最大整数），则方程:2006x+{x}= $\frac{1}{2007}$ 的实根的个数是( )．

A、O B、1 C、2 D、大于2的整数

查看试题解析

二、填空题

11. $- 27$ 的立方根为， $\sqrt{16}$ 的平方根为。

查看试题解析
12. 数2.185 $\times 10^{6}$ 精确到位.

查看试题解析
13. 若 $\sqrt[3]{3 m - 7} + \sqrt[3]{3 n + 4} = 0$ ，则m+n= ．

查看试题解析
14. 若a﹣b+6的算术平方根是2，2a+b﹣1的平方根是±4，则a﹣5b+3的立方根是.

查看试题解析
15. ①计算： $\sqrt{64} + \sqrt[3]{- 64} =$ ； ②比较大小： $\frac{\sqrt{5} - 3}{2}$ $\frac{\sqrt{5} - 2}{3}$ ；（选填“＞”“＜”或“＝”）

查看试题解析
16. 有一个数值转换器，原理如下图所示，当输入x的值为16时，输出y的值是．

查看试题解析
17. 若实数 $a ， b ， c$ 对应的点在数轴上的位置如图所示．请化简： $\sqrt{a^{2}} + | a + b | - | c - b | =$ ．

查看试题解析
18. 如图，在数轴上，点A、B表示的数分别为0、2，BC⊥AB于点B，且BC=1，连接AC，在AC上截取CD=BC，以A为圆心，AD的长为半径画弧，交线段AB于点E，则点E表示的实数是.

查看试题解析

三、解答题

19. 解方程：

(1)、 $3 {(x + 1)}^{2} = 75$

(2)、 ${(\frac{1}{3} x - 2)}^{2} = 125$

(3)、 ${(x - \sqrt{3})}^{2} = 2$

(4)、 $125 x^{3} + 343 = 0$

查看试题解析
20. 把下列各数填入相应的集合内：
$\sqrt{15}$ ，4， $\sqrt{16}$ ， $\frac{2}{3}$ ， $\sqrt[3]{27}$ ，0.15，-7.5，- $π$ ，0，2.3．
①有理数集合：｛                                               …｝；
②无理数集合：｛                                               …｝；
③正实数集合：｛                                               …｝；
④负实数集合：｛                                               …｝．

查看试题解析
21. 已知 $a$ ， $b$ ， $c$ 在数轴上的位置如图所示，请化简式子：
$\sqrt{a^{2}} - | a + b - c | + \sqrt{{(b + c)}^{2}} + | 2 b - c |$ ．

查看试题解析
22. 已知，M= $\sqrt{m + 4}$ 是9的算术平方根，N= $\sqrt[2 m + n + 4]{n + 10}$ 是n+10的立方根，求 $\sqrt{M - N}$ 的值．

查看试题解析
23. 甲同学用图3-①所示的方法作出了点C，表示数 $\sqrt{13}$ ，在△OAB中，∠OAB=90°，OA=2，AB=3，且点O，A，C在同一数轴上，OB=OC.

(1)、请说明甲同学这样做的理由；

(2)、仿照甲同学的作法，在图3-②所给的数轴上描出表示- $\sqrt{29}$ 的点A.

查看试题解析
24. 如图1，这是一个由27个同样大小的立方体组成的三阶魔方，体积为27．

(1)、求出这个魔方的棱长．

(2)、图中阴影部分是一个正方形ABCD，求出阴影部分的面积及其边长．

(3)、如图2，把图1中的正方形ABCD放到数轴上，使得点A与−1重合，那么点D在数轴上表示的数为．

查看试题解析
25. 如图，直径为1个单位长度的圆片上有一点 $Q$ 与数轴上的原点重合.（所有结果均保留 $π$ ）

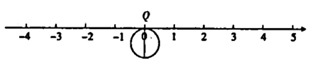(1)、若该圆片从原点沿数轴向左滚动一周，圆片上与原点重合的点 $Q$ 到达点 $Q^{'}$ ，设点 $Q^{'}$ 表示的数为 $a$ .
①求 $a$ 的值；

②求 $- (a - \sqrt{16}) - π$ 的算术平方根.

(2)、若圆片在数轴上向右滚动的周数记为正数，向左滚动的周数记为负数，依次滚动的情况记录如下：+2，-1，+3，-4，-3.
①第几次滚动后，点 $Q$ 距离原点最近？第几次滚动后，点 $Q$ 距离原点最远？

②当圆片结束运动时，点 $Q$ 运动的路程共有多少？此时点 $Q$ 所表示的数是多少？

查看试题解析
26. 细心观察图形，认真分析各式，然后解答问题．
OA₂²= ${(\sqrt{1})}^{2} + 1 = 2$ ， $S_{1} = \frac{\sqrt{1}}{2}$ ；

OA₃²=1²+ ${(\sqrt{2})}^{2} = 3$ ， $S_{2} = \frac{\sqrt{2}}{2}$ ；

OA₄²=1²+ ${(\sqrt{3})}^{2} = 4$ ， $S_{3} = \frac{\sqrt{3}}{2}$ …

(1)、请用含有n（n是正整数）的等式表示上述变规律：OA_n²=；S_n= ．

(2)、求出OA₁₀的长．

(3)、若一个三角形的面积是 $\sqrt{5}$ ，计算说明他是第几个三角形？

(4)、求出S₁²+S₂²+S₃²+…+S₁₀²的值．

查看试题解析

初中数学苏科版八年级上学期期末复习专题（8） 实数

一、单选题

二、填空题

三、解答题

初中数学苏科版八年级上学期期末复习专题（8）实数