湖南省长沙市雅礼教育集团2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-12-18 类型:期末考试
一、单选题
-
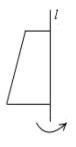
1. 在有理数1,0, , 中,是负数的为( )A、 B、 C、 D、2. 我国首艘国产航母于2018年4月26日正式下水,排水量约为65000吨,将65000用科学记数法表示为( )A、 B、 C、 D、3. 将如图所示的直角梯形绕直线l旋转一周,得到的立体图形是( )
 A、
A、 B、
B、 C、
C、 D、
D、 4. 下列结论正确的是( )A、 的系数是0 B、 中二次项系数是1 C、 的次数是5 D、 的次数是55. 下列等式变形错误的是( )A、若a=b,则 B、若a=b,则 C、若a=b,则 D、若a=b,则6. 如图,计划把河水引到水池A中,可以先引AB⊥CD , 垂足为B , 然后沿AB开渠,则能使所开的渠最短,这样设计的依据是( )
4. 下列结论正确的是( )A、 的系数是0 B、 中二次项系数是1 C、 的次数是5 D、 的次数是55. 下列等式变形错误的是( )A、若a=b,则 B、若a=b,则 C、若a=b,则 D、若a=b,则6. 如图,计划把河水引到水池A中,可以先引AB⊥CD , 垂足为B , 然后沿AB开渠,则能使所开的渠最短,这样设计的依据是( ) A、垂线段最短 B、两点之间,线段最短 C、两点确定一条直线 D、两点之间,直线最短7.
A、垂线段最短 B、两点之间,线段最短 C、两点确定一条直线 D、两点之间,直线最短7.如图,AB=8cm,AD=BC=5cm,则CD等于( )
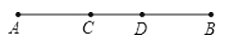 A、1cm B、2cm C、3cm D、4cm8. 已知 和 互补, 和 互补,且 ,那么( )A、 B、 C、 D、 与 的大小关系不确定9. 如图,不能判断 的条件是( )
A、1cm B、2cm C、3cm D、4cm8. 已知 和 互补, 和 互补,且 ,那么( )A、 B、 C、 D、 与 的大小关系不确定9. 如图,不能判断 的条件是( )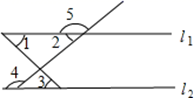 A、 B、 C、 D、10. 表示a、b两数的点在数轴上位置如图所示,则下列判断错误的是( )
A、 B、 C、 D、10. 表示a、b两数的点在数轴上位置如图所示,则下列判断错误的是( )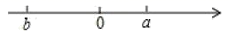 A、 B、 C、 D、11. 已知单项式 与 互为同类项,则 为A、1 B、2 C、3 D、412. 已知a,b,c是有理数,当 , 时,求 的值为( )A、1或-3 B、1,-1或-3 C、-1或3 D、1,-1,3或-3
A、 B、 C、 D、11. 已知单项式 与 互为同类项,则 为A、1 B、2 C、3 D、412. 已知a,b,c是有理数,当 , 时,求 的值为( )A、1或-3 B、1,-1或-3 C、-1或3 D、1,-1,3或-3二、填空题
-
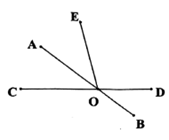
13. 有理数2019的倒数为.14. 如果∠α=35°,那么∠α的余角等于°.15. 已知x=2是关于x的方程2x﹣k=1的解,则k的值是 .16. 关于x,y的多项式 不含 的项,则a=.17. 如图,已知直线 相交于点 ,如果 , 平分 ,那么 度.
 18. 对于有理数,定义运算如下: ,则 .
18. 对于有理数,定义运算如下: ,则 .三、解答题
-
19. 计算:20. 解方程:21. 先化简,再求值: ,其中a=-1,b=1.22. 如图,直线AB、CD相交于点O,OM⊥AB.
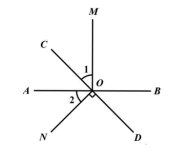 (1)、若∠1=∠2,证明:ON⊥CD;(2)、若 ,求∠BOD的度数.23. 如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD∥EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由.
(1)、若∠1=∠2,证明:ON⊥CD;(2)、若 ,求∠BOD的度数.23. 如图,AB⊥BD,CD⊥BD,∠A与∠AEF互补,以下是证明CD∥EF的推理过程及理由,请你在横线上补充适当条件,完整其推理过程或理由.
证明:∵AB⊥BD,CD⊥BD(已知)
∴∠ABD=∠CDB= ▲ ( )
∴∠ABD+∠CDB=180°
∴AB∥ ▲ ( )
又∠A与∠AEF互补 ( )
∠A+∠AEF= ▲
∴AB∥ ▲ ( )
∴CD∥EF ( )
24. 目前全国提倡环保,节能灯在城市已基本普及,某商场计划购进甲、乙两种节能灯共1000只,这两种节能灯的进价,售价如下表:进价(元/只)
售价(元/只)
甲型
25
30
乙型
45
60
(1)、如何进货,进货款恰好为37000元?(2)、为确保乙型节能灯顺利畅销,在(1)的条件下,商家决定对乙型节能灯进行打折出售,且全部售完后,乙型节能灯的利润率为20%,请问乙型节能灯需打几折?25. 定义:对于一个有理数x,我们把[x]称作x的对称数.若 ,则[x]=x-2:若x<0,则[x]=x+2.例:[1]=1-2=-1,[-2]=-2+2=0
(1)、求[ ][-1]的值;(2)、已知有理数a>0.b<0,且满足[a]=[b],试求代数式 的值:(3)、解方程:[2x]+[x+1]=126. 一套三角尺(分别含 , , 和 , , 的角)按如图所示摆放在量角器上,边 与量角器 刻度线重合,边 与量角器 刻度线重合,将三角尺 绕量角器中心点P以每秒 的速度顺时针旋转,当边 与 刻度线重合时停止运动,设三角尺 的运动时间为 .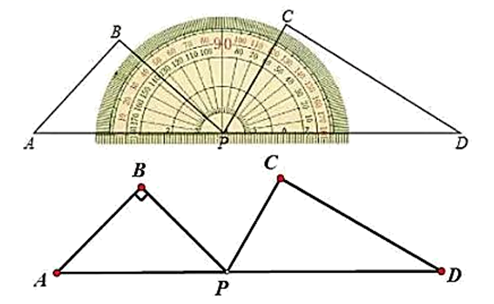 (1)、当 时,边 经过的量角器刻度线对应的度数是度;(2)、若在三角尺 开始旋转的同时,三角尺 也绕点P以每秒 的速度逆时针旋转,当三角尺 停止旋转时,三角尺 也停止旋转.
(1)、当 时,边 经过的量角器刻度线对应的度数是度;(2)、若在三角尺 开始旋转的同时,三角尺 也绕点P以每秒 的速度逆时针旋转,当三角尺 停止旋转时,三角尺 也停止旋转.①当t为何值时,边 平分 ;
②在旋转过程中,是否存在某一时刻使 ,若存在,请求出t的值;若不存在,请说明理由.