湖南省长沙市天心区长郡教育集团2019-2020学年七年级上学期数学期末试卷
试卷更新日期:2020-12-18 类型:期末考试
一、单选题
-
1. 2019的倒数是( )A、 2019 B、 C、 D、2. 某地一天早晨的气温是 ,中午温度上升了 ,半夜又下降了 ,则半夜的气温是( )A、 B、 C、 D、3. 在“北京2008”奥运会国家体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为460 000 000帕的钢材.将460 000 000用科学记数法表示为( )A、46×107 B、4.6×109 C、4.6×108 D、0.46×1094. 下列各组单项式中,不是同类项的是( )A、 与 B、 与 C、 与 D、 与5. 设 , ,若x取任意有理数,则A与B的大小关系为( )A、 B、 C、 D、无法比较6. 关于x的方程 =1的解为2,则m的值是( )A、2.5 B、1 C、-1 D、37. 已知方程7x+2=3x﹣6与x﹣1=k的解相同,则3k2﹣1的值为( )A、18 B、20 C、26 D、﹣268. 若“△”是新规定的某种运算符号,设x△y=xy+x+y,则2△m=﹣16中,m的值为( )A、8 B、﹣8 C、6 D、﹣69. 如图,点C在线段AB上,点E是AC中点,点D是BC中点.若ED=6,则线段AB的长为( )
 A、6 B、9 C、12 D、1810. 用度、分、秒表示 为( )A、 B、 C、 D、11. 如图,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,∠MON等于( )
A、6 B、9 C、12 D、1810. 用度、分、秒表示 为( )A、 B、 C、 D、11. 如图,∠AOB是平角,∠AOC=30°,∠BOD=60°,OM、ON分别是∠AOC、∠BOD的平分线,∠MON等于( ) A、90° B、135° C、150° D、120°12. 若不论k取什么实数,关于x的方程 (a、b是常数)的解总是x=1,则a+b的值是( )A、﹣0.5 B、0.5 C、﹣1.5 D、1.5
A、90° B、135° C、150° D、120°12. 若不论k取什么实数,关于x的方程 (a、b是常数)的解总是x=1,则a+b的值是( )A、﹣0.5 B、0.5 C、﹣1.5 D、1.5二、填空题
-
13. 数轴上表示 1 的点和表示﹣2 的点的距离是 .14. 如果 ,则 的值是 .15. 若 ,则 .16. 多项式2x4﹣(a+1)x3+(b﹣2)x2﹣3x﹣1,不含x3项和x2项,则ab= .17. 某商品每件标价为150元,若按标价打8折后,仍可获利20%,则该商品每件的进价为元.18. 甲、乙两队开展足球对抗赛,规定胜一场得3分,平一场得1分,负一场得0分,甲、乙两队共比赛6场,甲队保持不败,共得14分,甲队胜场.19. 已知线段 ,在直线 上画线段 ,则 的长是 .20. 如图,直线AB、CD相交于点O , OB平分∠EOD , ∠COE=100°,则∠AOC=°.

三、解答题
-
21. 计算
.
22. 解方程(1)、 ;(2)、 .23. 列方程解应用题(1)、某车间有24名工人,每人毎天平均生产螺栓12个或螺母18个,两个螺栓配三个螺母,为了使每天的产品刚好配套,应该分配多少名工人生产螺栓,多少名工人生产螺母?(2)、某校举行元旦汇演,七(01)、七(02)班各需购买贺卡70张,已知贺卡的价格如下:购买贺卡数
不超过30张
30张以上不超过50张
50张以上
每张价格
3元
2.5元
2元
(i)若七(01)班分两次购买,第一次购买24张,第二次购买46张,七(02)班一次性购买贺卡70张,则七(01)班、七(02)班购买贺卡费用各是多少元?哪个班费用更节省?省多少元?
(ⅱ)若七(01)班分两次购买贺卡共70张(第二次多于第一次),共付费150元,则第一次、第二次分别购买贺卡多少张?
24. 线段与角的计算(1)、如图,已知点C为 上一点, , ,若D、E分别为 、 的中点.求 的长.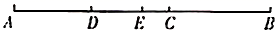 (2)、已知:如图, 被分成 , 平分 , 平分 ,且 ,求 的度数.
(2)、已知:如图, 被分成 , 平分 , 平分 ,且 ,求 的度数.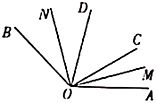 25. 已知多项式 的值与字母x的取值无关.(1)、求a,b的值;(2)、当 时,代数式的值为3,当 时,求代数式的值.26. 如图1,O为直线AB上一点,过点O作射线OC , ∠AOC=30°,将一直角三角板(∠D=30°)的直角顶点放在点O处,一边OE在射线OA上,另一边OD与OC都在直线AB的上方.
25. 已知多项式 的值与字母x的取值无关.(1)、求a,b的值;(2)、当 时,代数式的值为3,当 时,求代数式的值.26. 如图1,O为直线AB上一点,过点O作射线OC , ∠AOC=30°,将一直角三角板(∠D=30°)的直角顶点放在点O处,一边OE在射线OA上,另一边OD与OC都在直线AB的上方.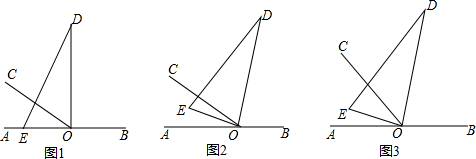 (1)、将图1中的三角板绕点O以每秒5°的速度沿顺时针方向旋转一周,如图2,经过t秒后,OD恰好平分∠BOC .
(1)、将图1中的三角板绕点O以每秒5°的速度沿顺时针方向旋转一周,如图2,经过t秒后,OD恰好平分∠BOC .此时t的值为;(直接填空)
(2)、此时OE是否平分∠AOC?请说明理由;(3)、在(1)问的基础上,若三角板在转动的同时,射线OC也绕O点以每秒8°的速度沿顺时针方向旋转一周,如图3,那么经过多长时间OC平分∠DOE?请说明理由;(4)、在(3)问的基础上,经过多长时间OC平分∠DOB?请画图并说明理由.