湖南省娄底市娄星区2019-2020学年七年级上学期数学期末试卷

试卷更新日期：2020-12-18 类型：期末考试

进入出卷网下载

一、单选题

1. 如果水库的水位高于正常水位5m时，记作+5m，那么低于正常水位3m时，应记作（　　）．

A、+3m B、-3m C、+3 D、-3

查看试题解析
2. $- 2019$ 的绝对值和相反数分别为（）．

A、2019，-2019 B、-2019，2019 C、2019，2019 D、-2019，-2019

查看试题解析
3. 下列调查方式，你认为最合适的是（）.

A、日光灯管厂要检测一批灯管的使用寿命，采用全面调查方式； B、旅客上飞机前的安检，采用抽样调查方式； C、了解娄底市居民日平均用水量，采用全面调查方式； D、对2019年央视春节联欢晚会收视率的调查，适合用抽样调查方式.

查看试题解析
4. 用代数式表示“ $m$ 的三倍与 $n$ 的差的平方”，正确的是（）

A、 ${(3 m - n)}^{2}$ B、 $3 {(m - n)}^{2}$ C、 $3 m - n^{2}$ D、 ${(m - 3 n)}^{2}$

查看试题解析
5. 下列说法中错误的个数有（　　）．
⑴-a表示负数； (2)多项式 $- 3 a^{2} b + 7 a^{2} b^{2} - 2 a b + 1$ 的次数是3；

⑶单项式 $- \frac{2 x y^{2}}{9}$ 的系数是-2；(4)2x²+3x-1是二次三项式.

A、1个 B、2个 C、3个 D、4个

查看试题解析
6. 已知 $2 x^{3} y^{1 - n}$ 与 $- 5 x^{3 m} y^{2}$ 是同类项，则式子 $m^{2018} - n^{2019}$ 的值是（）

A、2 B、1 C、0 D、-1

查看试题解析
7. 运用等式性质进行的变形，正确的是（　　）

A、若 $x = y$ ，则 $\frac{x}{c} = \frac{y}{c}$ B、若 $\frac{x}{c} = \frac{y}{c}$ ，则 $x = y$ C、由 $4 x - 5 = 3 x + 2$ ，得到 $4 x - 3 x = - 5 + 2$ D、若 $a^{2} = 3 a$ ，则 $a = 3$

查看试题解析
8. 方程 $\frac{2 x + 3}{2} - x = \frac{9 x - 5}{3} + 1$ 利用等式性质，正确的是（）

A、3（2x+3）-x=2（9x-5）+6 B、3（2x+3）-6x=2（9x-5）+1 C、3（2x+3）-x=2（9x-5）+1 D、3（2x+3）-6x=2（9x-5）+6

查看试题解析
9. 下列说法正确的是（）

A、画一条长3cm的射线； B、射线、线段、直线中直线最长 C、射线是直线的一部分 D、延长直线AB到C

查看试题解析
10. 在下列生活实例中：①在植树时,只要定出两个树坑的位置,就能使同一行树坑在一条直线上;②在正常情况下,射击时要保证瞄准的一只眼和两个准星在一条直线上,才能射中目标;③从甲地到乙地,原来是绕山而过,如今穿山修了一条笔直的隧道,节约了路程;④从A地到B地架设电线,总是尽可能沿着线段AB架设．其中能用“两点之间,线段最短”的数学依据来解释的现象有（）．

A、①③ B、②③ C、③④ D、②④

查看试题解析
11. 如图，点O在直线AB上，若∠AOC=3∠BOC，则∠BOC的度数为（）．

A、30° B、45° C、50° D、60°

查看试题解析
12. 学校有n名师生乘坐m辆客车外出参观，若每辆客车坐45人，则还有25人没有上车；若每辆客车坐50人，则刚好空出一辆客车．以下四个方程：① $45 m + 25 = 50 (m - 1)$ ；② $45 m - 25 = 50 (m - 1)$ ；③ $\frac{n - 25}{45} = \frac{n}{50} - 1$ ；④ $\frac{n - 25}{45} = \frac{n}{50} + 1$ ；其中正确的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. 据报道，“十、一”期间某市地铁二号线载客量达到1730000人次，再创历史新高．将数据1730000用科学记数法表示为.

查看试题解析
14. 已知直线 l 上有三点 A ， B ， C ，线段 AB=10cm，BC=6cm，点 M 是线段 BC 的中点，则 AM=cm.

查看试题解析
15. 为了解2019届本科生的就业情况某网站对 $2019$ 届本科生的签约情况进行了网络调查，至3月底参与网络调查的12000人中，只有5005人已与用人单位签约在这个网络调查中，样本容量是.

查看试题解析
16. 已知有理数 $a$ 在数轴上的位置如图所示，则化简 $a + | a - 1 |$ 的结果为.

查看试题解析
17. 如果方程 $(k - 2) x^{| 2 k - 3 |} - 3 = 0$ 是一个关于x的一元一次方程，那么k的值是．

查看试题解析
18. 按如图所示的方法用小棒摆正六边形，摆2个正六边形要11根小棒，摆3个正六边形要16根小棒，摆n个正六边形需要根小棒．

查看试题解析

三、解答题

19. 计算：

(1)、 $- 24 \div (- \frac{3}{2}) + 6 \times (- \frac{1}{3})$

(2)、 $| - 5 | + {(- 2)}^{3} - (\frac{2}{3} - \frac{1}{2}) \times (- 6)$

查看试题解析
20. 解方程

(1)、 $5 + 3 x = 7 (x - 1)$

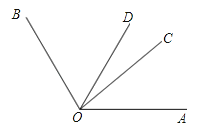
(2)、 $\frac{2 x + 1}{3} = \frac{x + 2}{4} - 1$

查看试题解析
21. 先化简，再求值：6x²﹣[3xy²+2（1﹣3xy²）+6x²]，其中x＝4，y＝﹣ $\frac{1}{2}$ ．

查看试题解析
22.
如图，已知∠BOC=2∠AOC，OD平分∠AOB，且∠AOC=40°，求∠COD的度数．

查看试题解析
23. 某城市按以下规定收取每月的水费：用水量如果不超过 10吨，按每吨 2.5元收费；如果超过 10吨，未超过的部分仍按每吨 2.5元收取，而超过部分则按每吨 3.5元收费．如果某用户 5月份水费平均为每吨 3.0元，那么该用户5月份用水多少吨?应交水费多少元？

查看试题解析
24. 春节是我国的传统节日，为了调查学生对于各地春节民俗活动的了解程度，某校抽取一部分学生进行问卷调查，将调查结果按“A：非常了解、B：基本了解、C：了解较少、D：不太了解”四类分别进行统计，并绘制出下面两幅不完整的统计图.请根据两幅统计图的信息，解答下列问题：

(1)、此次共调查了个学生；

(2)、扇形统计图中，A所在的扇形的圆心角度数为多少?；

查看试题解析
25. 已知两个分别含有30°，45°角的一幅直角三角板．

(1)、如图1叠放在一起，若∠CAD=4∠BAD，请计算∠CAE的度数；

(2)、如图2叠放在一起，使∠ACE=2∠BCD，请计算∠ACD的度数．

查看试题解析
26. 阅读理解：如图①，若线段AB在数轴上，A、B两点表示的数分别为a和b( $b > a$ ），则线段AB的长（点A到点B的距离）可表示为AB= $b - a$ .
请用上面材料中的知识解答下面的问题：如图②，一个点从数轴的原点开始，先向左移动2cm到达P点，再向右移动7cm到达Q点，用1个单位长度表示1cm．

(1)、请你在图②的数轴上表示出P，Q两点的位置；

(2)、若将图②中的点P向左移动xcm，点Q向右移动 $3 x$ cm，则移动后点P、点Q表示的数分别为多少？并求此时线段PQ的长.（用含x的代数式表示）；

(3)、若P、Q两点分别从第⑴问标出的位置开始，分别以每秒2个单位和1个单位的速度同时向数轴的正方向运动，设运动时间为t（秒），当t为多少时PQ=2cm？

查看试题解析